3617
Unsupervised Deep Learning Reconstruction Using the MR Imaging Model1Biomedical Engineering, State University of New York at Buffalo, Buffalo, NY, United States, 2Electrical Engineering, State University of New York at Buffalo, Buffalo, NY, United States, 3Program of Advanced Musculoskeletal Imaging (PAMI), Cleveland Clinic, Cleveland, OH, United States, 4Paul C. Lauterbur Research Center for Biomedical Imaging, SIAT, CAS, Shenzhen, China
Synopsis
Deep learning has been applied to MRI image reconstruction successfully. Most existing works require labeled ground-truth images to learn network parameters for image reconstruction, which is not practical in some MR applications where acquisition of fully sampled images takes too long. In this abstract, we propose a novel unsupervised deep neural network for reconstruction from undersampled data. The proposed network, named URED-net, is built upon conventional ADMM algorithm for compressed sensing reconstruction, but incorporating noise2noise, an unsupervised deep denoising network. The experimental results demonstrate proposed URED-net is superior to the standard noise2noise network with and without ground-truth images for training.
Introduction
Deep learning has recently demonstrated tremendous success in computer vision [1-2]. Inspired by such success, several studies have applied deep learning to MRI reconstruction from undersampled k-space data [3-10]. These studies use different neural networks to learn relationship between undersampled data and ground truth image using a large amount of training data. However, in some applications, it is very difficult to obtain a large number of ground truth images for training, such as in dynamic imaging and diffusion imaging. In this abstract, we proposed a novel unsupervised deep learning approach, named URED-net, to reconstruction from undersampled k-space data such that no ground-truth images are needed for training. The method is based on alternating direction method of multipliers (ADMM), a traditional optimizing algorithm for compressed sending reconstruction, but utilizing a powerful unsupervised denoising network noise2noise [11] in regularization functional. The proposed method takes advantage of both imaging equation (Fourier), prior model, and the powerful convolutional neural network trained on a large size of training data. It addresses the issue of artifacts and loss of resolution in reconstruction using noise2noise alone [last year abstract] by enforcing data consistency using state-of-the-art methods for inverse problems, such as plug-and-play priors and regularization by denoising methods. Experimental results demonstrate the proposed unsupervised deep reconstruction method outperforms competing methods (such as noise2noise with or without ground-truth training images) in term of reconstruction quality.Method
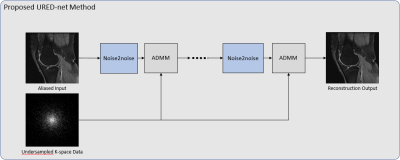
We start with the conventional compressed sensing MR reconstruction formulation $$\hat{x}=arg\underset{x}{min}\frac{1}{2}\left \| Ax-y \right \|_{2}^{2}+\lambda \rho\left ( x \right ) (1) $$ Where $$$\hat{x}$$$ is image to be reconstructed, $$$A$$$ is encoding matrix representing Fourier transform and undersampling matrix, $$$\lambda $$$ is regularization parameter and $$$\rho \left ( x \right )$$$ is regularization function. There are several algorithms to solve the optimization problem, such as the alternating direction method of multipliers (ADMM). Plug-and-Play Prior (P3) method [15-16] and Regularization by Denoising (RED) [17] have been proposed to leverage the power of an effective denoiser in optimization algorithm like ADMM. Specifically, reconstruction problem in (1) can be solved by sequentially applying image denoising steps (i.e., to use denoising methods to solve non-denosing problems). In particular, RED uses an existing denoiser to define an explicit image-adaptive Laplacian-based regularization functional, which is guaranteed to converge to globally optimal result.We propose to perform compressed sensing reconstruction using RED with Noise2Noise deep network as denoiser. Figure 1 illustrates the procedure to integrate noise2noise in the ADMM algorithm. With variable splitting and augmented Lagrangian method, the reconstruction problem becomes $$\hat{x}=arg\underset{x}{min}\frac{1}{2}\left \| Ax-y \right \|_{2}^{2}+\lambda\frac{1}{2}v^{T}\left ( v-D_{\theta}\left ( v \right ) \right )+\frac{\beta }{2}\left \| x-v+u \right \|_{2}^{2} (2) $$ where $$$\frac{1}{2}v^{T}\left ( v-D_{\theta}\left ( v \right ) \right )$$$ is the regularization function, $$$D_{\theta }$$$ is the noise2noise deep network with parameter $$$\theta$$$ learned from training images, and $$$u$$$ serves as the Lagrange multiplier vector for the set of constraints. Here we use ADMM to solve the problem in (2) by updating $$$x$$$, $$$v$$$ and $$$u$$$ iteratively as the following sub-problems: $$ \left\{\begin{matrix}\hat{x}=arg\underset{x}{min}\frac{1}{2}\left \| Ax-y \right \|_{2}^{2}+\frac{\beta }{2}\left \| x-v+u \right \|_{2}^{2}\\ \hat{v}=arg\underset{v}{min} \lambda\frac{1}{2}v^{T}\left ( v-D_{\theta}\left ( v \right ) \right )+\frac{\beta }{2}\left \| x-v+u \right \|_{2}^{2}\\ \hat{u}=u+x-v\end{matrix}\right. (3) $$ The network $$$D_{\theta}$$$ takes the aliased image from undersampled k-space data as the input and the desired clean image as output. Although $$$D_{\theta }$$$ can be any existing deep reconstruction networks, we adopt noise2noise deep network such that no ground-truth images are needed for training. The network is designed for complex images.
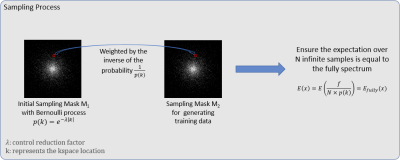
For training of the noise2noise network, we replace aliased(input)/ground-truth(target) training pair in conventional deep learning methods by the aliased(input)/aliased(target) training pair where the target is another aliased image from undersampled data but with a different random sampling mask. According to [12], to ensure such training is valid, a “Russian roulette” process, explained in Figure 2, is employed to generate random undersampling masks.
To evaluate performance of new method, we randomly selected 100 subjects from the NYU fastMRI dataset [18]. Among these datasets, 2000 left knee images were used for training and 450 images used for testing. A $$$5×$$$ random undersampling was used for both input and target during training and testing. Raw k-space data are used to reconstruct complex images. The hardware specification was CPU i7-6700K; Memory 48GB; GPU 1x NVIDIA GTX 1080TI. The training process takes 5 hours and reconstruction process takes less than 1 second.
Results
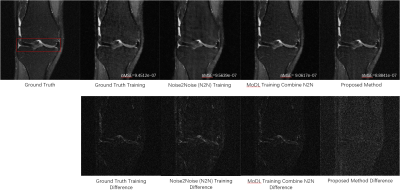
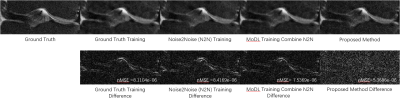
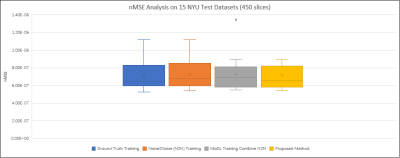
Figure 3 compares the reconstructions from three unsupervised learning methods: the proposed URED-net, MoDL [14] with N2N, and N2N [19] alone. Reconstructions with ground-truth training are also shown for comparison. Figure 4 shows the ROI and the corresponding difference images. Figure 5 shows the box-plot graph of the normalized mean square errors (NMSE) from 15 datasets (450 images). The statistical analysis reveals that proposed URED-net can achieve an error level similar to that using ground-truth training. The perceptual quality and the edge sharpness of the URED-net reconstructions are also close to those of the fully sampled reference.Conclusion
Our study demonstrates the feasibility of unsupervised deep learning for image reconstruction by combining RED with noise2noise. The proposed network is able to achieve similar reconstruction quality to those trained using ground-truth images. Future work will evaluate the proposed network on a large scale.Acknowledgements
The authors would like to thank the NYU group for making the MRI dataset available at https://fastmri.org/. This work is supported in part by the National Institute of Health U01EB023829.References
[1] O. Ronneberger, P. Fischer, and T. Brox, “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, 2015, pp. 234–241.
[2] C. Dong, C. C. Loy, K. He and X. Tang, "Image Super-Resolution Using Deep Convolutional Networks," in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 38, no. 2, pp. 295-307, 1 Feb. 2016.
[3] S. Wang, Z. Su, L. Ying, X. Peng, S. Zhu, F. Liang, D. Feng, D. Liang, “Accelerating magnetic resonance imaging via deep learning,” IEEE 14th International Symposium on Biomedical Imaging (ISBI), pp. 514-517, Apr. 2016.
[4] S. Wang, N. Huang, T. Zhao, Y. Yang, L. Ying, D. Liang, “1D Partial Fourier Parallel MR imaging with deep convolutional neural network,” Proceedings of International Society of Magnetic Resonance in Medicine Scientific Meeting, 2017.
[5] D. Lee, J. Yoo and J. C. Ye, “Deep residual learning for compressed sensing MRI,” IEEE 14th International Symposium on Biomedical Imaging (ISBI), Melbourne, VIC, pp. 15-18, Apr. 2017.
[6] Chang Min Hyun et al, “Deep learning for undersampled MRI reconstruction,” Phys. Med. Biol. 63 135007, 2018
[7] S. Wang, T. Zhao, N. Huang, S. Tan, Y. Liu, L. Ying, and D. Liang, “Feasibility of Multi-contrast MR imaging via deep learning,” Proceedings of International Society of Magnetic Resonance in Medicine Scientific Meeting, 2017
[8] Zhu, Bo, Jeremiah Z. Liu, Stephen F. Cauley, Bruce R. Rosen, and Matthew S. Rosen. "Image reconstruction by domain-transform manifold learning." Nature 555, no. 7697 (2018): 487.
[9] K. Hammernik, T. Klatzer, E. Kobler, M. P. Recht, D. K.Sodickson, T. Pock, and F. Knoll, “Learning a variational network for reconstruction of accelerated MRI data,”Magnetic Resonance in Medicine, vol. 79, no. 6, pp.3055–3071, 2018.
[10] K. H. Jin, M. T. McCann, E. Froustey and M. Unser, “Deep Convolutional Neural Network for Inverse Problems in Imaging,” in IEEE Transactions on Image Processing, vol. 26, no. 9, pp. 4509-4522, Sept. 2017.
[11] J. Lehtinen, J. Munkberg, J. Hasselgren, S. Laine, T. Karras, M. Aittala, T. Aila, “Noise2Noise: Learning Image Restoration without Clean Data,” Proceedings of the 35th International Conference on Machine Learning, PMLR 80:2965-2974, 2018.
[12] Zhang, Kai et al. “Learning Deep CNN Denoiser Prior for Image Restoration.” 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2017): 2808-2817.
[13] Diamond, Steven et al. “Unrolled Optimization with Deep Priors.” ArXiv abs/1705.08041, 2017
[14] Aggarwal, Hemant Kumar et al. “MoDL: Model-Based Deep Learning Architecture for Inverse Problems.” IEEE Transactions on Medical Imaging 38 (2017): 394-405.
[15] Y. Sun, B. Wohlberg and U. S. Kamilov, “An Online Plug-and-Play Algorithm for Regularized Image Reconstruction, ” in IEEE Transactions on Computational Imaging, vol. 5, no. 3, pp. 395-408, Sept. 2019. [16] Rizwan Ahmad et al. “Plug and play methods for magnetic resonance imaging (long version),” ArXiv abs/1903.08616
[17] Y. Romano, M. Elad, and P. Milanfar, “The Little Engine that Could: Regularization by Denoising (RED),” SIAM Journal on Imaging Sciences, 10(4), 1804–1844, 2017
[18] Zbontar, Jure et al. “fastMRI: An Open Dataset and Benchmarks for Accelerated MRI.” ArXiv abs/1811.08839 (2018): n. pag.
[19] P. Huang, C. Zhang et al, “Deep MRI Reconstruction without Ground Truth for Training”, International Society of Magnetic Resonance in Medicine Annual Meeting, #1235, 2019
Figures