Introduction

Deep neural networks have demonstrated their capabilities in reconstructing accelerated magnetic resonance (MR) image^1-5. However, models trained with mean-squared-error (MSE) or L1 loss tend to reconstruct smooth images while models trained with adversarial loss can recover rich textures but with unrealistic artefacts. To balance between these two effects, we employ a simple yet effective deep network interpolation approach which manipulates linear interpolation in the parameter space of multiple neural networks. We evaluate our method on a public multi-coil knee dataset from the fastMRI challenge⁶. Our results indicate that the strategy can effectively balance between data fidelity and perceptual quality.

Methods

The proposed source sensitivity network (SN) extends from the Deep-POCSENSE architecture proposed in [3]. It embeds the iterative optimisation scheme in a learning setting, which employs an unrolled architecture consisting of neural network based reconstruction blocks interleaved by data consistency (DC) layers. Specifically, the reconstruction block updates the estimate of the sensitivity weighted combined image, while DC is performed coil-wisely in k-space. In our work, the reconstruction block is modelled by a Down-Up network⁷ which has two complex-valued input and output channels. The network was trained with L1 and SSIM loss between reference image and the reconstruction$$$~x_{rec}$$$:$$L_{SN}(x_{rec},x_{ref})=SSIM(x_{rec},x_{ref})+\lambda{L_1(x_{rec},x_{ref})}.$$
To recover rich textures and details, we additionally propose to reconstruct images via an adversarial loss, where a discriminator is employed to identify if an input image is a fully sampled image or a reconstructed one. Specifically, we use the least squares generative adversarial network (LSGAN) for training the discriminator and reconstruction network in an adversarial way, as well as combining that with$$$~L_{SN}~$$$loss as a complementary metric. Then the network can be trained by minimising the following loss function:$$L_{SN-GAN}=\gamma{L_{SN}(x_{rec},x_{ref})}+L_{lsgan}(m\odot{x_{rec}},m\odot{x_{ref}}).~$$Here$$$~L_{lsgan}~$$$represents the LSGAN formulation and$$$~\odot~$$$is the pixel-wise product. We also introduce a binary foreground mask$$$~m~$$$to focus more on the texture of foreground regions.

However, we observed that models trained with$$$~L_{SN}~$$$loss tend to generate smooth images with relatively high quantitative scores, while those trained with$$$~L_{SN-GAN}~$$$loss can reconstruct images that contain better details and textures but with probably hallucinated artefacts. To balance between the quantitative and qualitative performances, we propose to interpolate the networks in the parameter space⁸. In detail, let$$$~\{G;\theta\}~$$$denote the mapping function of the image reconstruction model parameterised by$$$~\theta~$$$. Assume$$$~\{G^{SN};\theta_{SN}\}~$$$is the model trained with$$$~L_{SN}~$$$loss and$$$~\{G^{GAN};\theta_{GAN}\}~$$$is trained with$$$~L_{SN-GAN}~$$$loss, and both of them share the same network structure. To achieve a trade-off between effects of these two models, a linear interpolation of corresponding parameters is applied to derive a new interpolated model$$$~\{G^{interp};\theta_{interp}\}~$$$, where$$~\theta_{interp}=(1-\alpha)\theta_{SN}+\alpha{\theta_{GAN}},$$ with$$$~\alpha\in{[0,1]}~$$$as the interpolation coefficient. The interpolation is performed on all layers of the networks, including weights and biases. Note that the deep interpolation can be readily extended for multiple models with the same network architecture.

Experimental Settings

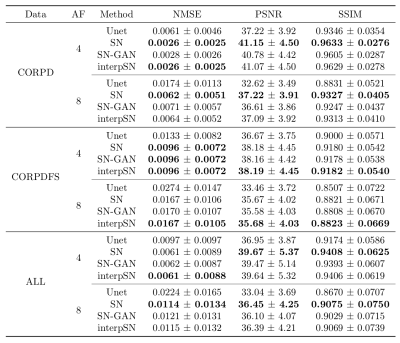
Evaluation was performed on a public knee dataset provided by the fastMRI challenge⁶. The dataset contains 973 volumes for training and 199 volumes for validation, including both coronal proton-density weighting with (PDFS) and without (PD) fat suppression. The multi-coil data contains 15 channel array data, and we used a variable density Cartesian undersampling scheme with acceleration factor (AF) 4 and 8. In our experiments, both SN and SN-GAN models were trained with a cascade number 10, and$$$~\lambda=10^{-3}~$$$and$$$~\gamma=0.1~$$$were chosen empirically. Specifically, SN model was first trained for 50 epochs using RMSProp with a learning rate$$$~10^{-4},~$$$and then both models were further finetuned based on the pretrained SN model for 10 epochs with a learning rate$$$~5\times{10^{-5}}.~$$$Here we use sensitivity encoing (SENSE) reconstruction⁹ as ground truth, as it generates better images than root-sum-of-squares (RSS) reconstruction.

Results

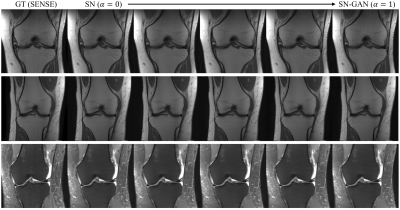
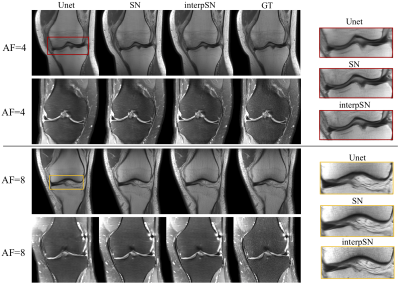
To examine the effect of the network interpolation, we present a group of qualitative results in Fig.1, showing the visual quality changes of the reconstructed images by varying$$$~\alpha~$$$from 0 to 1. Quantitative results are given in Table 1, where interpSN stands for the model that interpolates between SN and SN-GAN models with$$$~\alpha=0.5.~$$$It can be seen that the interpolated model improves over its source model SN in terms of the textures and also outperforms SN-GAN in terms of quantitative scores. By adjusting$$$~\alpha~$$$, it can achieve a smooth transitions between the two effects without abrupt changes. Fig.2 also displays the sample reconstructions for each acquisition and AF respectively, and it shows that our model outperformed the baseline Unet⁶ both quantitatively and qualitatively. Detailed visualisations indicate the capability of interpSN in recovering sharp textures over the other methods.

Discussion and Conclusion

In this work, we proposed to employ a simple deep network interpolation strategy for parallel MR image reconstruction. By interpolating networks in parameter space, we showed that the new interpolated model can balance between the quantitative scores and visual perception. It is worth noting that such interpolation scheme is at no cost, and the network architecture is flexible as long as the models to be interpolated share the same structure. By varying the interpolation coefficient, we can have a smooth control of the reconstruction effects, which could potentially enable the human observer to interpret based on the adjustment between perceptual quality and fidelity so that to ensure correct diagnosis. Future work can investigate on learning the interpolation coefficients to automatically find the optimal balance.

Acknowledgements

The work was funded in part by the EPSRC Programme Grant (EP/P001009/1) and by the Intramural Research Programs of the National Institutes of Health Clinical Center.