3615
Relax-ADMM-Net: A Relaxed ADMM Network for Compressed Sensing MRI1Research center for Medical AI, Shenzhen Institutes of Advanced Technology, shenzhen, China, 2Paul C. Lauterbur Research Center for Biomedical Imaging, Shenzhen Institutes of Advanced Technology, shenzhen, China, 3Department of Electronic Information Engineering, Nanchang University, Nanchang, China, 4Departments of Biomedical Engineering and Electrical Engineering, University at Buffalo,the State University of New York, Buffalo, NY, United States
Synopsis
ADMM is a popular algorithm for Compressed sensing (CS) MRI. ADMM-based deep networks have also achieved a great success by unrolling the ADMM algorithm into deep neural networks. Nevertheless, ADMM-Nets only make the components in the regularization term learnable. In this work, we propose a relaxed version of ADMM-Net (i.e. Relax-ADMM-Net) to further improve its performance for fast MRI, where the additional data consistency term and variable combinations in the updating rules are all freely learned by the network. Experiments reveal the effectiveness of the proposed network compared with several competing model-driven networks.
Introduction
Compressed sensing (CS) is a popular strategy for fast MR imaging [1]. The classical CS-MRI models may undergo loss of structures and details, especially at high accelerating rates. To mitigate this problem, many endeavors have been made [2]-[6]. However, these methods still have limitations in reconstruction time, regularization parameter and sparsifying transform selection. ADMM-Net, one of the pioneer works in model-driven deep learning networks was proposed to alleviate these issues by first unrolling the ADMM iteration procedure to a deep network [9]. Then, the regularization parameter, sparsifying transform and regularizer can be learned from network training [10]-[13]. Although ADMM-net and its variant have achieved success in fast MR imaging, there is still room to further improve its performance. In this work, we propose a relaxed version of ADMM-Net (i.e. Relax-ADMM-Net) by additionally learning the data consistency term and variable combinations in the updating rules. Experimental results show that the proposed method can achieve superior performance than several model-driven networks with learning restricted in the regularization term.Theory and method
Assume $$$m{\in}{\mathbb{C}}^M$$$ is a MR image to be reconstructed, $$$f{\in}{\mathbb{C}}^N(N<M)$$$ is the under-sampled k-space data, and introducing a set of independent auxiliary variables $$$z={\{z_1,z_2,...,z_L}\}$$$ in the spatial domain, ADMM reconstructs the image by solving the following sub-problems:$$ \begin{cases}agrmin_{m}{\frac{1}{2}}{||Am-f||^2_2}+{\frac{\rho}{2}{||m+\beta-z}||^2_2}\\agrmin_{z}{\sum_{l=1}^L}{||{\lambda}_l{\psi}_lz||_p}+ {\frac{\rho}{2}{||m+\beta-z}||^2_2}\\agrmin_{\beta}{\sum_{l=1}^L}<\beta,m-z>\end{cases} (1)$$
where $$$A$$$ is the encoding matrix, $$${\psi}_l$$$ denotes a transformation matrix (e.g., discrete wavelet transform) and $$$0{\leq }p{\leq}1$$$. $$${\lambda}_l$$$ denotes the regularization parameter and $$${\rho}$$$ is a penalty parameter. ADMM-Net was designed by unrolling the iterative optimization procedure of the Eq. (1). The original network, denoted as basic-ADMM-CSNet, learns the regularization parameters in the ADMM algorithm [9]. It was then improved as Eq. (2) by learning the image transformation and regularizer in the regularization term in their follow-up work, denoted as Generic-ADMM-CSNet [10].
$$\begin{cases}M^{(n)}:m^{(n)}={\frac{A^Tf+{\rho}(z^{(n-1)}-{\beta}^{(n-1)})}{A^TA+{\rho} I}}\\Z^{(n)}:z^{(n)}={\mu_{1}}z^{(n,k-1)}+\mu_{2}(m^{(n)}+{\beta}^{(n-1)})-{\sum_{l=1}^L}{{\lambda}_l{{\psi}_l}^T||{\psi}_lz^{(n,k-1)}||_p}\\P^{(n)}:{\beta}^{(n)}=\beta^{(n-1)} +\eta(m^{(n)}-z^{(n)})\end{cases} (2)$$
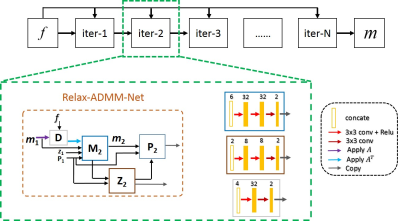
In this work, we further boost the ADMM-Net by 1)relaxing the constraint of data consistency term and 2)breaking the combination structure of variables. In detail, the data consistency is no longer measured by the L2 norm as $$$||Am-f||^2_2$$$, but is learned from the training data. In addition, the fixed variable combinations in the first and second updating steps are broken, and are also freely learned by the network. Mathematically, the updating rules of the proposed Relax-ADMM-Net can be formulated as:
$$\begin{cases}D^{(n)}:d^{(n)}=\Gamma(Am^{(n-1)},f)\\M^{(n)}:m^{(n)}=\Pi(m^{(n-1)},z^{(n-1)}-\beta^{(n-1)},A^Td^{(n)})\\Z^{(n)}:z^{(n)}=\Lambda (m^{(n)}+\beta^{(n-1)})\\P^{(n)}:{\beta}^{(n)}=\beta^{(n-1)} +\eta(m^{(n)}-z^{(n)})\end{cases} (3)$$
where operators $$$\Gamma$$$ , $$$\Pi$$$, and $$$\Lambda$$$ as well as the parameter $$$\eta$$$ are all accomplished by the neural network. The framework of Relax-ADMM-Net is depicted in Fig. 1.
Experiment
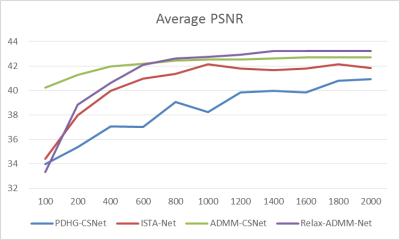
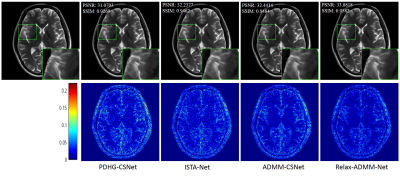
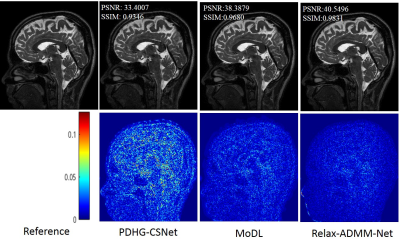
The proposed Relax-ADMM-Net was first compared with three model-driven networks PDHG-CSNet [12], ISTA-Net [7], and Generic-ADMM-CSNet (called ADMM-CSNet hereafter) for single-channel MR imaging. Overall 2100 fully sampled multi-contrast data from 3T SIEMENS scanner were collected for training. 398 human brain 2D data from SIEMENS 3T scanner and 15 human brain 2D data from United Imaging Healthcare (UIH) 3T scanner were used for testing. All of these data were adaptively combined to single-channel data [14] and retrospectively down-sampled with the Poisson disk sampling mask. Especially, the networks were trained at 6x sampling rate and tested on the data from SIEMENS and UIH with 6x and 10x acceleration, respectively. Furthermore, Relax-ADMM-Net was also evaluated on the 12-channel T2-weighted brain data from the reference [11] for multi-channel MR image reconstruction. In this part, the PDHG-CSNet and MoDL [11] were used for comparison. They were all trained with 360 2D data and tested on 164 2D data at a 6x Poisson disk sampling rate. Peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) were used to evaluate the restored results.Result Average PSNR values of the networks evaluated on 398 brain data from the SIEMENS scanner are shown in Fig. 2. It is obvious that the performance of each network becomes better as the number of training samples increasing. Relax-ADMM-Net achieves the best scores when the training data size is larger than 800. A 2D slice from UIH data at 10x acceleration is displayed in Fig. 3. As can be seen from the quantitative values and reconstruction errors, the proposed network preserves more details than the competing methods. It is because the data consistency and variable combinations learned from the network are more suitable for the under-sampled data than the predefined ones. Similar conclusion can be drawn in Fig. 4, which displays a 2D reconstruction from under-sampled multi-channel brain data.
Conclusion
This work proposed a relaxed ADMM-Net network for fast MRI. The relaxations on the data consistence term and variable combination structure of ADMM greatly boost the reconstruction performance. Preliminary experiments demonstrate its effectiveness both in visual inspection and quantitative measures.Acknowledgements
This work was supported by the National Natural Science Foundation of China (U1805261), National Key R&D Program of China (2017YFC0108802) and the Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000).References
[1]. Lustig M, Donoho D, Pauly J M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007; 58: 1182-1195.
[2]. Liang D, Liu B, Wang J, et al. Accelerating SENSE using compressed sensing. Magn. Reson. Med. 2009; 62.6: 1574-1584.
[3]. Ravishankar S, Bresler Y. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Trans. on Medical Imaging 2011; 30(5):1028-1041.
[4]. Liang D, Wang H, Chang Y, et al. Sensitivity encoding reconstruction with nonlocal total variation regularization. Magn. Reson. Med. 2011; 65(5):1384-1392.
[5]. Wang S, Liu J, Liu Q, et al. Iterative feature refinement for accurate undersampled MR image reconstruction. Phys. Med. Biol. 2016; 61(9):3291-3316.
[6]. Cheng J, Jia S, Ying L, et al. Improved parallel image reconstruction using feature refinement. Magn. Reson. Med. 2018; 80(1): 211-223.
[7]. Zhang J and Ghanem B. ISTA-Net: Interpretable optimiza-tion-inspired deep network for image compressive sensing. CVPR 2018.
[8]. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn. Reson. Med. 2017; 79(6).
[9]. Yang Y, Sun J, Li H, and Xu Z. Deep ADMM-Net for compressive sensing MRI. Neural Information Processing Systems, pp. 10-18, 2016.
[10]. Yang Y, Sun J, Li H, and Xu Z. ADMM-CSNet: A deep learning approach for image compressive sensing. IEEE Trans Pattern Anal Mach Intell 2018; Nov, 28.
[11]. Aggarwal H, Mani, and Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans. on Medical Imaging 2019; 38: 394-405.
[12]. Cheng J, Wang H, Ying L, and Liang D. Model Learning: Primal Dual Networks for Fast MR Imaging. MICCAI, pp. 21-29 2019..
[13]. Liu Y, Liu Q, Zhang M, Yang Q, Wang S and Liang D. IFR-Net: iterative feature refinement network for compressed sensing MRI. arXiv preprint arXiv:1909.10856, 2019.
[14]. Walsh D, Gmitro A, and Marcellin M. Adaptive reconstruction of phased array MR imagery. Magn. Reson. Med. 2000; 43: 682-690.
Figures