Introduction

MR image reconstruction is an ill-posed inverse problem and prone to errors especially when only sparse and limited data are available and/or in the presence of large measurement noise. Machine learning (ML) based methods provide promising solutions to the problem, exploiting significant prior images available in various applications. An important strength of deep learning networks lies in their power and flexibility in representing and learning complex image priors from training data.^1-2 However, ML image priors are often inaccurate due to limited training data and high dimensionality of image functions. As a result, direct ML-based reconstructions can produce large reconstruction errors.³ To alleviate this problem, a common strategy is to integrate the ML-based solution into the conventional constrained reconstruction framework via a regularization function.^4-7 In this work, we treat ML-based reconstruction as an initial estimate and use an information theoretical framework to incorporate it into the final reconstruction, which is optimized to capture novel image features. The proposed method has been validated in multiple MR image reconstruction applications and produced very encouraging results. It may provide an effective framework for ML-based image reconstruction.

Method

We decompose the desired image function $$$\rho(\boldsymbol{x})$$$ into two components, one absorbing the ML-based image priors and the other capturing any localized novel features:
$$\hspace{16em}\rho(\boldsymbol{x})=f(\rho_{\text{ML}}(\boldsymbol{x}))+\rho_{\text{n}}(\boldsymbol{x})\hspace{16em}$$
$$\hspace{22em}\text{subj.}\:\text{to}\:\left\lVert{W}\rho_{\text{n}}\right\rVert_0\leq\delta.\hspace{22.25em}(1)$$
The first term is a function of the solution provided by the pre-trained neural networks (NN) and the second term is a sparse component under some sparsifying transformation $$$W$$$.

Derivation of the functional form of $$$f(\cdot)$$$
The specific functional form of $$$f(\cdot)$$$ is derived under the minimum cross-entropy principle. More specifically, we treat the ML-based solution $$$\rho_{\text{ML}}(\boldsymbol{x})$$$ as an initial estimate for $$$\rho(\boldsymbol{x})$$$ and the optimal reconstruction is the one minimizing the cross-entropy measure under data-consistency constraint:
$$\min_{\rho(\boldsymbol{x})}\int\rho(\boldsymbol{x})\log\frac{\rho(\boldsymbol{x})}{\rho_{\text{ML}}(\boldsymbol{x})}d\boldsymbol{x}$$
$$\hspace{19em}\text{subj.}\:\text{to}\:d(m\Delta\boldsymbol{k})=\int\rho(\boldsymbol{x})e^{i2\pi{m}\Delta\boldsymbol{k}\boldsymbol{x}}d\boldsymbol{x}.\hspace{17.5em}(2)$$
The motivation for the use of minimizing cross-entropy principle is that it forces any new image features added to the solution to have evidence from the measured data.⁷ It can be proved that the solution to Eq. (2) takes the following form:
$$\hspace{17.5em}\bar{\rho}(\boldsymbol{x})=\rho_{\text{ML}}(\boldsymbol{x})\text{exp}\left(\sum_{m}c_{m}e^{i2\pi{m}\Delta\boldsymbol{k}\boldsymbol{x}}-1\right),\hspace{17.25em}(3)$$
which can be approximated by:
$$\hspace{19.5em}\bar{\rho}(\boldsymbol{x})\approx\rho_{\text{ML}}(\boldsymbol{x})\sum_{m}c_{m}e^{i2\pi{m}\Delta\boldsymbol{k}\boldsymbol{x}}.\hspace{20.25em}(4)$$
Eq. (4) is also known as the generalized series (GS) model.⁹ As a result, the functional form of $$$f(\cdot)$$$ is chosen to be $$$f(\rho_{\text{ML}})=\rho_{\text{ML}}(\boldsymbol{x})\sum_{m}c_{m}e^{i2\pi{m}\Delta\boldsymbol{k}\boldsymbol{x}}$$$.

Capturing localized novel features using sparsity
The GS model can be also interpreted as a finite impulse response (FIR) filter. It effectively captures the low-frequency (smooth) discrepancies between $$$\rho(\boldsymbol{x})$$$ and $$$\rho_{\text{ML}}(\boldsymbol{x})$$$, for example, the shading effect caused by B₁ inhomogeneity. However, there also exist some localized novel features in practice that cannot be compensated by Eq. (3), such as focal lesions. To make our model complete, we further introduce a sparse term $$$\rho_{\text{n}}(\boldsymbol{x})$$$ as described in Eq. (1) to capture such local novel features. The two terms in Eq. (1) synergistically compensate for each other in the reconstruction process and enable the model to utilize prior information effectively for the sake of capturing novel features.

Constrained image reconstruction
The proposed signal model leads to a constrained image reconstruction formulated as:
$$\hspace{10em}\{\bar{c}_{m}\},\bar{\rho}_{\text{n}}=\arg\min_{\{c_m\},\rho_{\text{n}}}\left\lVert{d}-\Omega{F}\{\rho_{\text{ML}}(\boldsymbol{x})\sum_{m}c_{m}e^{i2\pi{m}\Delta\boldsymbol{k}\boldsymbol{x}}+\rho_{\text{n}}(\boldsymbol{x})\}\right\rVert_2^2+\lambda\left\lVert{W}\rho_{\text{n}}\right\rVert_1,\hspace{8.5em}(5)$$
where $$$d$$$ is the measured data, $$$\Omega$$$ the sampling operator and $$$F$$$ the Fourier operator. The final estimate can be synthesized as $$$\hat{\rho}(\boldsymbol{x})=\rho_{\text{ML}}(\boldsymbol{x})\sum_{m}\bar{c}_{m}e^{i2\pi{m}\Delta\boldsymbol{k}\boldsymbol{x}}+\bar{\rho}_{\text{n}}(\boldsymbol{x})$$$.

Results

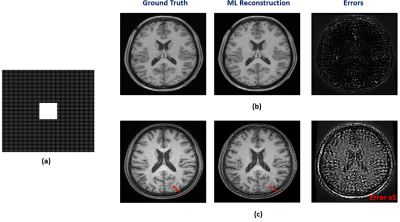
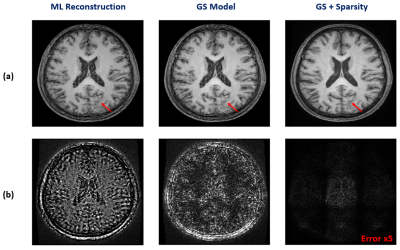
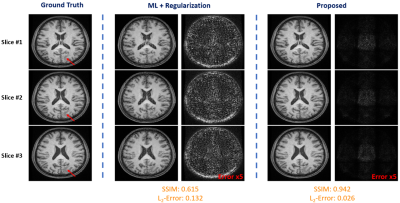
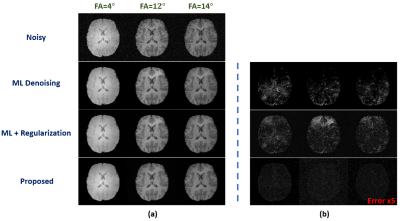
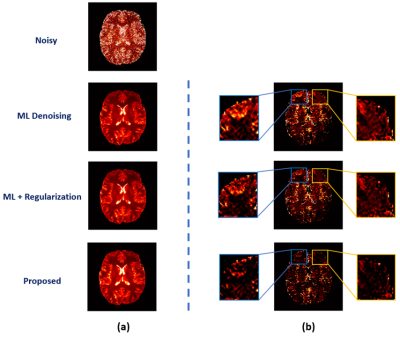
We have first evaluated our method in sparse image reconstruction. In this experiment, we adopted a dual-density sampling scheme with 15% sparsity (Fig. 1a). To obtain the ML-based image priors, we trained a DAGAN¹⁰ using the HCP database, with the Fourier reconstruction as the input. Two testing datasets have been used here: the one from the HCP database (not seen during training) and the one we collected from a tumor patient using similar imaging protocol as in HCP. As shown in Fig. 1, the network did a reasonable job for the testing data from HCP, but performed significantly worse on the tumor data. Figure 2 illustrates how each term in Eq. (1) overcame the limitations of ML-based reconstruction in processing tumor data. As can be seen, the low-order discrepancies were well captured by the first term and the residuals became much sparser and thus easier to be captured by the second term. Figure 3 compares the proposed method with the traditional strategy that integrates the ML-based prior using regularization, from which we can see the superior performance of the proposed method.
We have also tested the proposed method in the context of image denoising for T1 mapping. The training datasets were acquired using FLASH sequences with variable flip angles (FA=4°,12° and 14°). In this experiment, we trained a pix2pix GAN¹¹ to predict FLASH images from the associated MPRAGE images. Figure 4 compares different image denoising methods and Figure 5 illustrates the corresponding T1 maps and the associated error maps. Again, the proposed method resulted in the best performance.

Conclusions

This paper presents a new method for ML-based MR image reconstruction. The proposed method decomposes the desired image function into two terms, one incorporating the ML-based image priors under minimum cross-entropy principle and the other capturing the localized novel features with sparsity term. The proposed method has been validated in multiple applications and produced impressive results. It may provide an effective framework for ML-based image reconstruction.

Acknowledgements

This work reported in this paper was supported, in part, by the following research grants: NIH-R21-EB023413 and NIH-U01-EB026978.