Introduction

MR images have phase distribution due to inhomogeneities of static field strength and the difference of magnetic susceptibility, therefore image reconstruction must consider phase on the image as well as its magnitude. D. Lee et al. proposed deep convolutional neural network (CNN) reconstruction in which magnitude and phase distribution are reconstructed independently[1], and　Y. Yang et al. proposed ADMM-CSnet for reconstructing phase varied images using multi-layer network [2]. Since phase function is periodical ($$$-\pi, \pi$$$) non smooth function, it is not easy to estimate precise distribution from under-sampled signal, and ADMM-CSnet require quite long time for learning the manner of artifacts appearances. In this paper, we propose a novel CNN image reconstruction in the information of phase distribution is not required and complex images can be reconstructed using only real-value single CNN.

Method

MR signal $$$s({\bf k})$$$ can be expressed as Eq.(1) ,

$$s({\bf k})=\int \rho({\bf x}) e^{-j \phi({\bf x})} e^{-j({\bf k \cdot x)}} d{\bf x}\nonumber ={\cal F}\left[ \rho({\bf x}) e^{-j \phi({\bf x})} \right] ...(1),$$

where $$$\bf k$$$ is a k-space vector and $$$\bf x$$$ is a space vector, $$$\rho({\bf x})$$$ is spin density distribution, $$$\phi({\bf x})$$$ is the function of phase variation due to imperfection in the MRI equipment and inhomogeneities in the main static magnetic field and $$${\cal F}$$$ is the operator of the Fourier transform.
The real and imaginary part of the complex image $$$\rho({\bf x}) \exp^{-j \phi({\bf x})} $$$ can be written as follows:

$${\cal F}\left\{ {\rm Re} \left[ \rho({\bf x}) e^{-j \phi({\bf x)}} \right] \right\} =\!\frac{1}{2}{\cal F}\left\{ \rho({\bf x}) e^{-j \phi({\bf x)}}\!\! +\!\! \rho({\bf x}) e^{j \phi({\bf x)}} \right\} =\frac{1}{2} \left\{ s({\bf k})+s({-\bf k})^{*} \right\} ...(2),$$ $${\cal F}\left\{{\rm Im}\! \left[ \rho({\bf x}) e^{-j \phi({\bf x)}} \right] \right\} =-\frac{j}{2} {\cal F}\left\{ \rho({\bf x}) e^{-j \phi({\bf x)}}\!\! - \!\! \rho({\bf x}) e^{j \phi({\bf x)}} \right\} =-\frac{j}{2} \left\{ s({\bf k})-s(-{\bf k})^{*} \right\} ...(3),$$

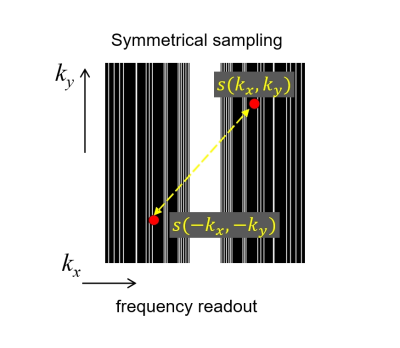
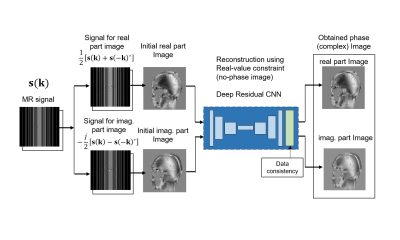
In this paper, we focus on Cartesian grid sampling, which is the most widely used technique. If a symmetrical signal sampling with respect to the origin of k-space is executed as shown in Fig.1, then the real and imaginary part of complex image can be reconstructed independently of each other by corresponding signal [3], which means that estimation of phase distribution on the image is unnecessary and real-value constraint can be used in each part of image. Based on these relation, a novel compressed sensing image reconstruction method is proposed in which real and imaginary part of complex images are reconstructed independently using a single CNN. Since estimation of phase distribution is not necessary and real-value constraint can be used in the reconstruction procedure, proposed method is robust to phase changes on the image and easy for training of images. Figure 2 show the structure of proposed method. For the architecture of CNN, residual learning and batch normalization [4] was used for learning. The depth of CNN was set 30 and corresponding receptive field size was 61x61. Three types of layers were used, (1) Conv+ReLU: for the first layer, 64 filters of size 3 x 3, 2) Conv+BN+ReLU: for layers 2 ~ 29, 64 filters of size 3 x 3 x 64, 3) Conv: for the last layer, 3x3x64 filter were used. Data consistency step is incorporated at the end of network since each part of complex image correspond to signal calculated using the relation of Eq.(2) and (3).

Results & Discussions

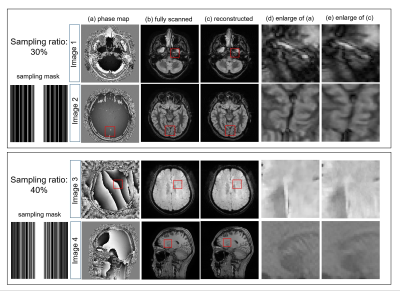
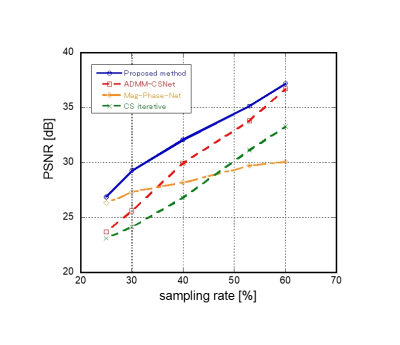
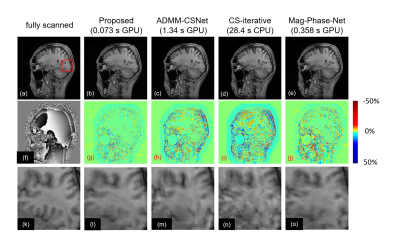
MR normal volunteer images were collected using a Toshiba 1.5T MRI scanner. MR signals are calculated using the acquired phase varied images by applying Fourier transform in the simulation experiments. Real part and imaginary part of complex images are used together for the training of single CNN. The number of images for CNN training is 50 including real part and imaginary part of 25 complex images. Various phase images with rapid or slow phase changes are used for CNN training. Figure 3 shows the representative results using 30% and 40% signal with various phase images. It was shown that fairly good images with small aliasing artifacts are obtained irrespective of the magnitude of phase change. We compared the peak-signal-to-noise ratio (PSNR) of obtained images with other reconstruction methods; magnitude and phase CNN (Mag&phase) method [1], ADMM-CSNet [2] and iterative phase and magnitude optimization method (CS iter) [5]. Symmetrical k-space random sampling was used for proposed method and other methods use non-symmetrical random sampling. The results of PSNR evaluation is summarized in Fig.4 and the comparison of reconstructed images using 30% signal are shown in Fig.5. Reconstruction time of each method is shown inside the parenthesis. Reconstructed images, error mages and enlarged images are shown in top, middle and bottom rows, respectively. Remained aliasing artifacts are very small and details of the object are reconstructed well in proposed method. Figure 4 shows that highest PSNRs are obtained in proposed method in all signal sampling rates.

Conclusion

A novel phase varied image reconstruction method using symmetrical k-space sampling with single CNN is proposed. It was demonstrated that high quality images with smaller artifacts were obtained. Proposed method is highly practical since it is robust to phase variation and is easy for training because of its simple CNN structure.

Acknowledgements

This study was supported in part by JSPS KAKENHI(19K04423). We would like to thank Canon Medical Systems.