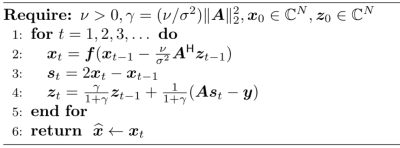INTRODUCTION

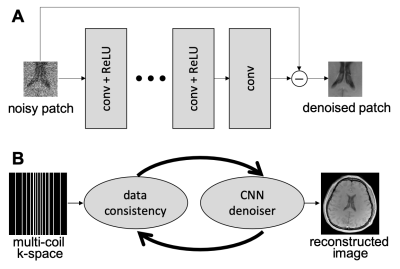
Plug-and-play (PnP) methods [1] can leverage the power of deep learning (DL) by employing learned, application-specific denoisers [2]. A high-level description of the combination of PnP and DL, termed PnP-DL, is shown in Figure 1. Compared to compressed sensing (CS), PnP-DL can generate images with higher quality. Compared to other DL methods, the performance of PnP-DL is robust of variations in the sampling pattern or sensitivity maps. However, the performance of PnP-DL is sensitive to changes in the measurement signal-to-noise ratio (SNR) and algorithmic parameters that balance the contributions from the data fidelity and denoising terms. We present a discrepancy-principle-based technique that auto-tunes the contribution of the denoiser in PnP reconstruction, leading to a parameter-free recovery.

METHODS

Traditional CS methods recover an image, $$$\boldsymbol{x}\in\mathbb{C}^N$$$, by solving the following optimization problem.
$$ \widehat{\boldsymbol{x}} = \arg\min_{\boldsymbol{x}} \big\{\frac{1}{2\sigma^2}\|\boldsymbol{A}\boldsymbol{x}-\boldsymbol{y}\|_2^2+\phi(\boldsymbol{x})\big\},\quad \quad (1)$$
where $$$\boldsymbol{A}\in\mathbb{C}^{M\times N}$$$ is the sensing matrix, $$$\boldsymbol{y}\in\mathbb{C}^M$$$ is measured multi-coil k-space data, $$$\sigma^2$$$ is noise variance estimated from a pre-scan, and $$$\phi(\boldsymbol{x})$$$ is a sparsity-base regularizer. Many algorithmic choices are available to solve Equation 1, including the primal dual splitting (PDS) algorithm [3], which is outlined in Figure 2. For PnP reconstruction, the "proximal" operator $$$\boldsymbol{f}(\boldsymbol{z}) = \arg\min_{\boldsymbol{x}} \{\phi(\boldsymbol{x}) + \frac{1}{2\nu}\|\boldsymbol{x}-\boldsymbol{z}\|^2_2\}$$$ in PDS is replaced with a call to a denoising subroutine.

For a plug-in denoiser, the choice of $$$\nu$$$ in PDS affects the solution. We propose to tune $$$\nu$$$ based on Morozov's discrepancy principle (DP) [4], i.e., $$$\nu$$$ is updated within each iteration, $$$t$$$, of PDS using $$$\nu_t = \nu_{t-1}\, \|\boldsymbol{A}\boldsymbol{x}_t-\boldsymbol{y}\|^2_2/(M \sigma^2)$$$. The motivation behind DP is to promote the residual norm, $$$\|\boldsymbol{A}\boldsymbol{x}_t-\boldsymbol{y}\|^2_2$$$, to approach the norm of the additive Gaussian noise, which is expected to be $$$M\sigma^2$$$. The pseudo-code for the modified PDS algorithm is given in Figure 3. The PnP-DL method that uses DP to adapt $$$\nu$$$ is termed as PnP-DL-DP.

For validation, we first collected a fully sampled segmented cardiac cine dataset from a 3T ( MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany) scanner. The dataset was retrospectively undersampled (R=8) and reconstructed with PnP-DL using an application-specific DL denoiser. As described in [2], the denoiser was trained by performing denoising on spatial-temporal image patches that were corrupted with additive Gaussian noise. All PnP-DL reconstructions were performed with PDS for eight different values of $$$\nu$$$ and PDS with DP. The normalised mean square error (NMSE) for each reconstruction was defined as $$$20\log_{10}\|\boldsymbol{x}-\widehat{\boldsymbol{x}}\|_2/\|\boldsymbol{x}\|_2$$$. Then, we collected three prospectively undersampled (R=6$$$-$$$12), free-breathing real-time cine datasets at 3T, 1.5T ( MAGNETOM Avanto, Siemens Healthcare, Erlangen, Germany), and 0.35T (ViewRay, Oakwood, Ohio) scanners, resulting in nine datasets. The data were collected using a prototype sequence with pseudo-random Cartesian sampling. For all datasets, the noise variance, $$$\sigma^2$$$, was estimated from a sub-second pre-scan. These datasets were reconstructed using PDS with a fixed value of $$$\nu$$$ that had led to the smallest error in the retrospectively undersampled 3T dataset, as well as PDS with DP and a parameter-free CS method called SCoRe [5]. For PnP, 200 iterations were employed. The reconstruction results were evaluated by an expert on a five-point Likert scale (1: non-diagnostic, 2: poor, 3: adequate, 4: good, 5: excellent).

RESULTS

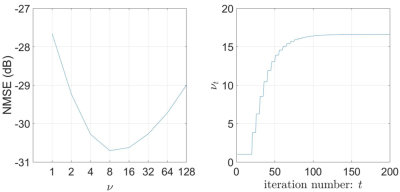
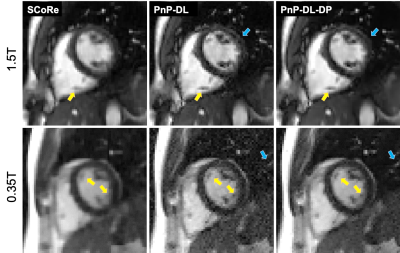
Figure 4 (left) highlights the performance dependency of PnP-DL on $$$\nu$$$, with the higher values yielding noisier and low values yielding smoother images. The NMSE is lowest at $$$\nu=8$$$. For PnP-DL-DP, Figure 4 (right) shows the adaptation of $$$\nu_t$$$, which converges to the value of 16.6 after approximately 100 iterations. The NMSE value of PnP-DL-DP is only 0.1 dB worse than that of PnP-DL with $$$\nu=8$$$. For the prospectively undersampled datasets at 3T, SCoRe, PnP-DL, and PnP-DL-DP received average scores of 4, 4, and 4, respectively. For 1.5T, these methods received average scores of 3.67, 3.37, and 4, respectively. For 0.35T, these methods received average scores of 2.33, 1.67, and 3, respectively. Figure 5 shows representative frames from 1.5T and 0.35T datasets.

DISCUSSION

The performance of PnP-DL-DP is only marginally (0.1 dB) inferior compared to PnP-DL with manually tuned $$$\nu$$$. The scoring by an expert indicates that PnP-DL and PnP-DL-DP have similar performance at 3T, which is not surprising because the value of $$$\nu$$$ was manually optimized on a 3T dataset. The relative performance of PnP-DL degrades at lower SNR (field strength), with two out of three PnP-DL images at 0.35T receiving a score of one (non-diagnostic). This is because the value of $$$\nu$$$ optimized for a high-SNR dataset is suboptimal for datasets with significantly different SNR. Figure 5 demonstrates that PnP-DL-DP exhibits more consistent performance across field strengths, while PnP-DL becomes progressively noisy at lower field strengths. Also, in comparison to SCoRe, which is a parameter-free CS method, PnP methods can preserve fine details.

CONCLUSION

The algorithms available to solve the PnP problem admit at least one parameter that controls the relative contributions from the data fidelity and denoising terms. Here, we utilize DP to adaptively tune the parameter $$$\nu$$$ in PDS. Our preliminary results show that DP-based parameter tuning yields consistent performance despite significant changes in the measurement SNR. PnP-DL-DP is equally applicable to other MRI applications and can be extended to other PnP algorithms such as alternating direction method of multipliers.

Acknowledgements

This work was funded by NIH R01HL135489.