Introduction

The connection between deep neural network and the Ordinary Differential Equation (ODE) has been studied and discussed in different recent works [1,2,3,4,5,6]. It has been shown that residual networks such as ResNet [7] and recurrent neural network decoders can be modeled as a discretization of a continuous ODE model. An ODE-based model and its relation to the residual network can be shown as follows:
$$\text L_{t_1} =\text L_{t_0} + f(\text L_{t_0},\theta) \ \ \ (ResNet) \ \ \ (1)$$
$$\text L_{t_1} =\text L_{t_0} + \int_{t_0}^{t_1} f(\text L_{t},\theta)\ dt \ \ \ (ODE) \ \ \ (2)$$
where $$$\text L_{t_0}, \text L_{t_1}$$$ are the residual block input and output. $$$f$$$ represents the network-defined nonlinear operator which preserves the dimensionality of $$$\text L_{t_0}$$$ and $$$\theta$$$ represents the network weights. The defined ODE ($$$\frac{d\text L}{dt} = f(\text L_{t},\theta)$$$) is described in terms of its solution in $$$t=t_1$$$. The forward step of ODE Euler discretization is as follows:
$$\text L_{t_{0}+h} =\text L_{t_0} + hf(\text L_{t_0},\theta) \ \ \ (3)$$
It can be observed that the single forward step of Eq.3, can be considered as the equivalent to the formulation of the residual block. Therefore, The ODE discretization model can lead to different ODE-inspired network architectures. In this paper, we present an ODE-based deep network for Magnetic Resonance Imaging (MRI) reconstruction which extends the conventional reconstruction framework to its data-adaptive variant using the ODE-based network and provides an end-to-end reconstruction scheme. We evaluate the reconstruction performance of our method to the reconstruction methods based on the standard UNet network [8] and Residual network.

Methods

The discretized version of MR imaging model given by
$$\text d=\text E \text x + \text n. \ \ \ (4)$$
where $$$\text x$$$ is the samples of unknown MR image, and $$$\text d$$$ is the undersampled k-space data. $$$\text E =\text {FS}$$$ is an encoding matrix, and $$$\text F$$$ is an undersampled Fourier operator. $$$\text S$$$ is a matrix representing the sensitivity map of the coils, and $$$\text n$$$ is noise. Assuming that the interchannel noise covariance has been whitened, the reconstruction relies on the least-square approach:
$$\hat{\text x} =\underset{\text x}{ argmin} \ \|\text d-\text E\text x\|_{2}^{2} \ \ \ (5)$$
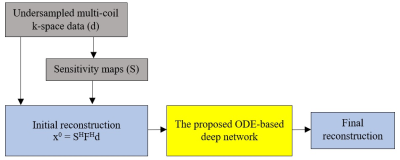
The ODE-based reconstruction framework we used for solving the Eq.5 is shown in Figure 1.
For a conventional neural network, we minimize the loss function ($$$l$$$) over a set of training pairs and we search for the weights ($$$\theta$$$) that minimize that loss function:
$$\underset{\theta}{ minimize} \ \frac{1}{M} \sum\limits_{i=1}^M l(L(\theta;x_i,y_i)) + \text R(\theta) \ \ \ (6)$$
where $$$(x_i,y_i)$$$ is the $$$i_{th}$$$ training pairs (input and ground truth). $$$R$$$ is a regularization operator and $$$M$$$ is the number of training pairs. The loss function depends implicitly on $$$\theta$$$. This optimization is usually solved through Stochastic Gradient Descent (SGD) and backpropagation to compute the gradient of $$$L$$$ with respect to $$$\theta$$$. In our ODE-based network, besides the $$$L$$$s, the network weights also change with respect to time as well. In this case, we need to solve the following constrained optimization problem:
$$\underset{p,\theta}{ minimize} \ \frac{1}{M} \sum\limits_{i=1}^M l(L_{t_1};x_i,y_i) + \text R(p,\theta) \ \ \ (7)$$
$$\frac{d\text L}{dt} = f(\text L_{t},\theta_{t}) \ \ \ (8)$$
$$\frac{d\theta}{dt} = w(\theta_{t},p) \ \ \ (9)$$
where $$$\theta_t$$$ is parameterized by the learnable dynamics of
$$\theta_{t_1} =\theta_{t_0} + \int_{t_0}^{t_1} w(\theta_{t},p)\ dt \ \ \ (10)$$
where $$$w$$$ is a nonlinear operator responsible for the network weights dynamics and $$$p$$$ is the parameters for $$$w$$$. We also augment the learnable space and solve the ODE flow as follows so that the learned ODE representation won't preserve the input space topology [5].
$$\frac{d}{dt} \begin{bmatrix} \text L\\ a \end{bmatrix} = f(\begin{bmatrix} \text L_{t}\\ a_{t} \end{bmatrix},\theta_{t}) \ \ \ (11)$$
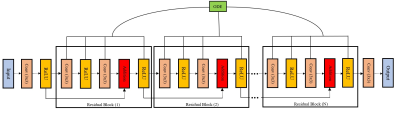
where $$$a_{0}=0$$$. We use the discretize-then-optimize method [4,6] to calculate the gradients for backpropagating through ODE layers. Figure 2 shows the proposed ODE-based deep network. Five residual blocks have been used in our method (N=5).

Results

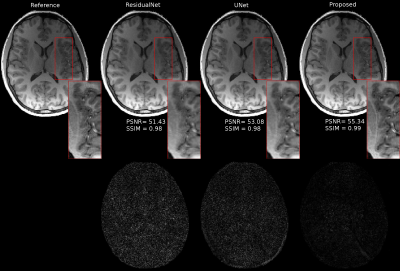
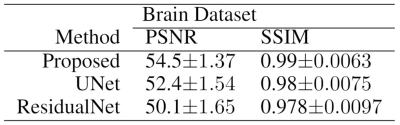
In our experiments, we have tested our method with our MPRAGE brain datasets. The data on ten volunteers with a total of 750 brain images used as the training set. Images from fifteen different patients have used as the testing set. The sensitivity maps were computed from a block of size 24x24 using the ESPIRiT [9] method. Reconstruction results with the undersampling factor of 2x2 for different approaches are shown in Figure 3. ResidualNet includes the same number of residual blocks as our proposed method (without ODE layers). Table 1 shows that our method consistently has higher Peak Signal-to-noise Ratios (PSNR) and structural similarities (SSIM) compared to the reconstructions using the other two networks.

Conclusion

In conclusion, an ODE-based deep network for MRI reconstruction is proposed. It enables the rapid acquisition of MR images with improved image quality. The proposed ODE-based network can be easily adopted by unrolled optimization schemes for better MRI reconstruction accuracy.

Acknowledgements

This research was supported in part by NIH grants R01 NS079788, R01 EB019483, R01 DK100404, and by a research grant from the Boston Children's Hospital Translational Research Program and a pilot grant (PP-1905-34002) from National Multiple Sclerosis Society.