3602
Multi-contrast MR imaging with enhanced denoising autoencoder prior network learning1Department of Electronic Information Engineering, Nanchang University, Nanchang, China, 2Paul C. Lauterbur Research Center for Biomedical Imaging, SIAT, Chinese Academy of Sciences, Shenzhen, China, 3Department of Biomedical Engineering and Electrical Engineering, The State University of New York, Buffalo, New York, NY, United States
Synopsis
This paper proposes an enhanced denoising autoencoder prior (EDAEP) network learning method for multi-contrast MR reconstruction using deep learning. Specifically, a multi-model autoencoder with various noise levels was developed to capture different features from multi-contrast images. A weighted aggregation strategy was also adopted to balance the impact of multiple model outputs. These designs empower the network to explore the correlations and similarities among multi-contrast images, handle different acceleration trajectories and avoid a lot of cumbersome retraining. Experimental results demonstrate that our method can improve the quality of reconstructed images compared to other classical methods.
INTRODUCTION
Multi-contrast magnetic resonance imaging (MRI) plays a very important role in clinical analysis and diagnosis1. However, the relatively long time of acquiring multiple contrast images greatly limits its wide applications. Classical compressed sensing (CS) based methods exploit joint total variation (TV) regularization1,2 and group sparsity3 in corresponding transform domains to accelerate MR imaging. Although certain successes have been achieved, most methods reconstruct each contrast with limited prior knowledge considered and the reconstruction is still very time-consuming. To solve this, some deep learning based multi-contrast MR imaging methods have been proposed4,5. However, they tend to be very sensitive to noise attacks and have to be retrained when the sampling patterns or acceleration factors change. To enhance the generalization capability of deep learning models, this paper proposes a multi-model autoencoder with different noise level stimulation based on denoising autoencoder (DAE)6 for multi-contrast MRI. The multi- noise stimulation further boosts the capacity and robustness of the model, where small noise level encourages the network to better preserve fine structure with less denoising power and high noise level forces the network to capture coarse scale features with strong noise removal capability.METHOD
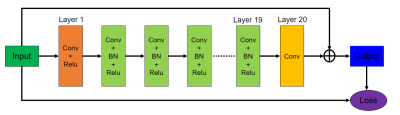
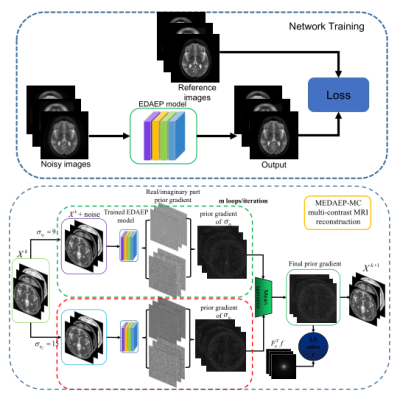
The method mainly consists of two phases: an offline training phase and an online testing phase. For the offline period, we try to train a multi-noise autoencoder prior with the consideration of different noise levels to capture features of different scales including local fine-grained and global coarse-grained features. A reweighted average strategy is also employed to balance the impact of each other, therefore the training loss of multi-noise models for the prior term $$$G(.)$$$ can be given as $$$L_{MEDAE} = E_{\eta,X} [\frac{1}{N}\sum\limits_{i=1}^{N}\left\|X-D_{\sigma_{\eta_i}}(X)\right\|^2],N=2$$$, where $$$X=[x_1,x_2,x_3]$$$ denote the multi-contrast images (PD/T1/T2 contrast) and $$$D_{\sigma_{\eta_i}}(X)$$$ denotes the output of DAE network with the noise levels of $$$\sigma_{\eta_i}$$$. For the online testing phase, we use the learned prior to do the multi-contrast MR reconstruction. The mathematical model for online testing is $$$\min_{X}\sum\limits_{l=1}^{T}\left\|F_{u_l}x_l-f_l\right\|^2+\frac{\lambda}{N}\sum\limits_{i=1}^{N}\left\|X-D_{\sigma_{\eta_i}}(X)\right\|^2$$$, which can be solved iteratively as (i) $$$X^k = X^{k-1}-{M[\nabla G(X^{k-1})]}/m$$$ and (ii) $$$\ X^{k+1}\ = \mathop{\arg\min}_{X}\sum\limits_{l=1}^{T}\left\|F_{u_l}x_l-f_l\right\|^2+\lambda\left\|X-X^k\right\|^2$$$. Here $$$M$$$ denotes the mean operation applied to the prior gradient, $$$X^k$$$ represents the intermediate result obtained in the $$$k$$$-th iteration, $$$N$$$ is the number of noise model, $$$m$$$ is the number of loops per iteration and $$$T$$$ is the number of contrast images. Finally, we update the reconstructed k-space data via (iii) $$$\frac{\lambda S_0(k_x,k_y)+S_1(k_x,k_y)}{1+\lambda}$$$ if the k-space location $$$(k_x,k_y)$$$ has been sampled, otherwise remain unchanged, where $$$S_0(k_x,k_y)$$$ is the corresponding zero-filled k-space measurements of multi-contrast images. Fig. 1 illustrates the network architecture of original denoising autoencoder which consists of 20 convolutional layers. The detailed flowchart of the proposed multi-contrast training and reconstruction phase is shown in Fig. 2.EXPERIMENT
All experiments were performed on two public MRI datasets: SRI24-spm87 and Brainweb8. SRI24-spm8 dataset was acquired on a 3.0T GE scanner with different parameter settings. For PD/T2 weighted images: 2D axial dual-echo fast spin echo (FSE) sequence, TR = 10s, TE = 14/98 ms, the field-of-view (FOV) is 240×240 mm, slice thickness = 2.5 mm; For T1 weighted images: 3D axial IR-prep Spoiled Gradient Recalled (SPGR) sequence, TR = 6.5 ms, TE = 1.54 ms, FOV = 240×240 mm, thickness = 1.25 mm. Brainweb is a Simulated Brain Database (SBD) which consists of MR data volumes with various slice thicknesses, noise levels and intensity non-uniformity levels. All images were resized to 256×256 and the two datasets are mixed to compose the final dataset. We randomly select 80% for training, 15% for validation, and the rest of 5% for testing. The implementation was conducted using Caffe framework and MATLAB 2017a with TITAN XP on Intel(R) Xeon(R) CPU E5-2640 @ 2.40GHz×16.RESULTS AND DISCUSSION
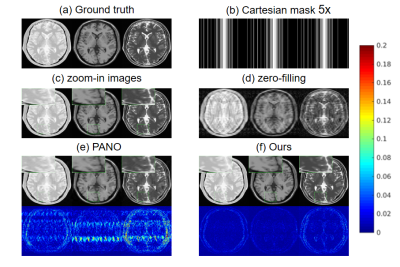
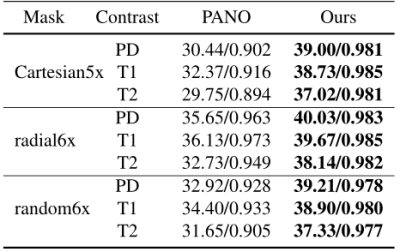
Fig. 3 shows the reconstruction results of PANO9 and our method under 1D Cartesian masks with 20% subsampling. As can be seen from the zero filling direct reconstruction results, the multi-contrast images are highly corrupted. PANO can remove most of the artifacts that are visiable in zero-filling reconstruction, but the result is still blurred and some aliasing artifacts can be easily seen. The result obtained by our method preserves more details and tissue structures. The error map of each contrast further shows the strength of our method in preserving details and fine structures. We also tested our method with different sampling patterns and acceleration factors. Table I also demonstrates our method can get better results.CONCLUSION
In this work, we propose an enhanced denoising autoencoder prior framework for multi-contrast MRI reconstruction, where multiple noise levels are used to stimulate the network training with weighted aggregation strategy. The method can effectively explore the correlations and similarities among multi-contrast images to boost the capacity and robustness of the model. The experiments demonstrate that our method can provide both better quantitative and qualitative results which are beneficial to clinical diagnosis. The extension to more different type of contrasts (like FLAIR, diffusion weighted imaging (DWI) ) will be our future work.Acknowledgements
This research was partially supported by the National Natural Science Foundation of China (61601450, 61871371, 81830056), Science and Technology Planning Project of Guangdong Province (2017B020227012, 2018B010109009), Youth Innovation Promotion Association Program of Chinese Academy of Sciences (2019351), and the Basic Research Program of Shenzhen (JCYJ20180507182400762).References
1. Huang J, Li R, Li Y, Fang R, Zhang S, Pan H et al. Fast Preconditioning for Accelerated Multi-contrast MRI Reconstruction. Proc. MICCAI. 2015;707-709.
2. Bilgic B, Chatnuntawech I, Martin A, Setsompop K, Adalsteinsson E, Schiaviet E et al. Vectorial total generalized variation for accelerated multi-channel multi-contrast MRI. Magnetic Resonance Imaging. 2016;34(8):1161-1170.
3. Huang J, Chen C, Axel L et al. Fast Multi-contrast MRI Reconstruction. Proc. MICCAI. 2012;281-288.
4. Wang S, Zhao T, Huang N, Tan S, Liu Y, Ying L, Liang D et al. Feasibility of Multi-contrast MR imaging via deep learning. Proc. ISMRM. 2017;3985.
5. Sun L, Fan Z, Fu X, Huang Y, Ding X and Paisley J et al. A Deep Information Sharing Network for Multi-Contrast Compressed Sensing MRI Reconstruction. IEEE Transactions on Image Processing. 2019;28(12):6141-6153.
6. Bigdeli S, Jin M, Favaro P, Zwicker M et al. Deep Mean-Shift Priors for Image Restoration. Proc. NeurIPS. 2017.
7. Rohlfing T, Zahr N, Sullivan E, Pfefferbaum A et al. The SRI24 multichannel atlas of normal adult human brain structure. Human Brain Mapping. 2010;31(5):798.
8. Cocosco C, Kollokian V, Kwan K, Evans A et al. BrainWeb: Online Interface to a 3D MRI Simulated Brain Database. Neuroimage. 1997;5:425.
9. Qu X, Hou Y, Lam F, Guo D, Zhong J, Chen Z et al. Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator. Medical Image Analysis. 2014;18(6):843-856.
Figures