3599

Uncertainty Quantification for Deep MRI

Vineet Edupuganti¹, Morteza Mardani¹, Joseph Cheng¹, Shreyas Vasanawala², and John Pauly¹
¹Electrical Engineering, Stanford University, Stanford, CA, United States, ²Radiology, Stanford University, Stanford, CA, United States

Synopsis

Reliable MRI reconstruction is crucial for accurate diagnosis. However, high resolution imaging leaves substantial uncertainty about the authenticity of the recovered pixels especially when using overparameterized deep learning. Leveraging variational autoencoders (VAEs), this study proposes a Bayesian imaging algorithm that distills the uncertainty in a low-dimensional latent code. One can then simply draw independent samples from the decoder to procure pixel variance maps along with the image. To further quantify the prediction risk of unseen images, we adopt Stein's Unbiased Risk Estimator (SURE), which we find correlates well with the true risk.

Introduction

Reliable medical image recovery is a major challenge in Magnetic Resonance Imaging (MRI) due to heavy undersampling of the acquired images. As a result, the last several years have witnessed an explosion of deep learning (DL) reconstruction approaches that offer orders of magnitude speed-up while simultaneously improving accuracy.^1,2,3,4,5,6 One major shortcoming of these studies, however, is a lack of focus on the robustness of DL architectures in inverse problems. Not only is the introduction of image artifacts fairly common using such models, but there do not currently exist suitable statistical methods that enable the quantification of uncertainty.⁷ This lack of appropriate tools to estimate risk in reconstructions is especially problematic given the sensitive nature of medical imaging, where artifacts in recovered images could mislead radiologists and result in incorrect patient diagnoses.

Problem Statement: Given an observation $$$y$$$, we want to recover an image $$$x_0$$$, where $$$y = \Phi x_0$$$ ($$$\Phi = \Omega F$$$, the product of a subsampling mask and the Fourier operator), $$$y\in \mathcal{C}^m$$$, $$$x_0\in \mathcal{C}^n$$$, and $$$m \ll n$$$. The objective of this work is to evaluate the uncertainty associated with obtaining $$$x_0$$$ (see Fig. 1).

Contributions: To this end, this work introduces procedures to evaluate DL reconstruction robustness. In doing so, we first develop a VAE-GAN model for MR image recovery. We then use Monte Carlo methods to analyze the variations and errors in the output image distribution with different hyperparameters, before introducing SURE as a new technique for gauging DL model uncertainty.

Model

For image recovery, we consider a GAN architecture, where the VAE serves as the generator function $$$\mathcal{G}$$$ and a CNN as the discriminator $$$\mathcal{D}$$$ (see Fig. 2). This architecture has the advantage of effectively modeling high-frequency components that are important in MR images.⁷ To ensure these reconstructions did not deviate from physical measurement, data consistency was applied to all network outputs, which was essential in obtaining high SNR. The data consistent subspace was obtained by applying an affine projection based on the undersampling mask.⁷ The VAE was chosen as the generator function to learn a probability distribution of realistic images. The loss functions used in training were based on both pixel-wise $$$\ell_2$$$ and adversarial GAN loss:
$$\min_{\Theta_d} E_{x}\left[(1-\mathcal{D}(x;\Theta_d))^{2}\right] + E_{y}\left[(\mathcal{D}(\hat{x};\Theta_d))^{2}\right]$$
$$\min_{\Theta_g} E_{x,y} (1-\lambda)\left[\|x-\hat{x}\|_{2} + \eta D_{KL}(\mathcal{N}(\mu_x,\sigma_x)\|\mathcal{N}(0,1)) \right] + \lambda E_{y}\left[(1 - \mathcal{D}(\hat{x};\Theta_d))^{2}\right]$$

Methods

Monte Carlo variance maps: An effective way of analyzing uncertainty in inverse problems is to examine the variability of the recovered images.⁸ Utilizing the probabilistic nature of the VAE-GAN model, for a given input we can draw samples from the resulting output distribution. This Monte Carlo sampling approach allows one to evaluate variance as well as higher order statistics, which can be very useful in understanding the extent and impact of model uncertainty.

Denoising SURE: In addition to Monte Carlo analysis, an underexplored statistical technique for computing risk when the ground truth is unknown is Stein's Unbiased Risk Estimator (SURE), which has seen little to no prior application in medical imaging.⁹ Using SURE we can obtain an unbiased estimate of risk ($$$E(SURE) = MSE$$$).
$$SURE = -n\sigma^2 + \underbrace{\|\hat{x}-x_{\rm zf}\|^2}_{\text{RSS}} + \sigma^2\underbrace{{\rm tr}(\frac{\partial \hat{x}}{\partial x_{\rm zf}})}_{\text{DOF}}$$
This form importantly does not depend on $$$x_0$$$ and approximates degrees of freedom (DOF) with the trace of the Jacobian (gradient of output w.r.t. the input zero-filled image), which can be easily computed.

Evaluations

Dataset: The Knee dataset used was obtained from $$$19$$$ patients with a 3T GE MR750 scanner.¹⁰ Each volume consisted of 320 2D slices of dimension $$$320\times256$$$, and a 5-fold variable density undersampling mask with radial view ordering (designed to preserve low-frequency structural elements) was used to produce aliased input images $$$x_{\rm zf}$$$ for the model to reconstruct.¹¹

Network architecture: The VAE encoder and decoder were each composed of $$$4$$$ layers formed through a sequence of strided convolution and transpose convolution operations, respectively, while the discriminator was an 8-layer CNN.

Variance maps: Using the Monte Carlo method described earlier, 1K outputs corresponding to different reference slices were generated after training by feeding a test image into the model and sampling from the resulting output distribution. Figure 3 shows a representative uncertainty map (as measured by variance), which can provide a quantifiable confidence score. However, to accurately compute error, we must know the bias (i.e. difference between the reconstruction and ground truth), which is not possible in a clinical setting.

SURE: Due to the shortcomings of the Monte Carlo approach, we evaluate the SURE estimate on our test images, noting that this technique can be applied when the ground truth is unknown and is relevant for both deterministic and generative models. Figure 4 shows the tradeoff between RSS and DOF (bias and variance), as well as the relationship between the true risk as defined by MSE and the SURE estimate. We see that there is a strong correlation between MSE and SURE for the given sample of test images, indicating that SURE is indeed a valuable approximation of error. These results are highly promising and can be used to offer additional context during diagnosis. Ongoing work is focused on extending the SURE approach to produce pixel maps that can be directly used in a clinical setting.

Acknowledgements

This work was supported by NIH Grant R01EB009690, NIH Grant R01EB026136, and GE Healthcare.

References

Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434, 2015.
Tran Minh Quan, Thanh Nguyen-Duc, and Won-Ki Jeong. Compressed sensing MRI recon- struction with cyclic loss in generative adversarial networks. arXiv preprint arXiv:1709.00753, 2017.
Bo Zhu, Jeremiah Z Liu, Stephen F Cauley, Bruce R Rosen, and Matthew S Rosen. Image reconstruction by domain-transform manifold learning. Nature, 555(7697):487, 2018.
Dongwook Lee, Jaejun Yoo, and Jong Chul Ye. Deep residual learning for compressed sensing mri. In Biomedical Imaging (ISBI 2017), 2017 IEEE 14th International Symposium on, pages 15–18. IEEE, 2017.
Ashish Bora, Ajil Jalal, Eric Price, and Alexandros G Dimakis. Compressed sensing using generative models. arXiv preprint arXiv:1703.03208, 2017.
Ali Mousavi, Ankit B Patel, and Richard G Baraniuk. A deep learning approach to structured signal recovery. In Communication, Control, and Computing (Allerton), 2015 53rd Annual Allerton Conference on, pages 1336–1343. IEEE, 2015.
Morteza Mardani, Enhao Gong, Joseph Y Cheng, Shreyas S Vasanawala, Greg Zaharchuk, Lei Xing, and John M Pauly. Deep generative adversarial neural networks for compressive sensing (GANCS) MRI. IEEE Transactions on Medical Imaging, 2018.
Alex Kendall and Yarin Gal. What uncertainties do we need in bayesian deep learning for computer vision? In Advances in neural information processing systems, pages 5574–5584, 2017.
Ryan J Tibshirani and Saharon Rosset. Excess optimism: How biased is the apparent error of an estimator tuned by SURE? Journal of the American Statistical Association, pages 1–16, 2018.
http://mridata.org/.
Joseph Y Cheng, Tao Zhang, Marcus T Alley, Michael Lustig, Shreyas S Vasanawala, and John M Pauly. Variable-density radial view-ordering and sampling for time-optimized 3d cartesian imaging. In Proceedings of the ISMRM Workshop on Data Sampling and Image Reconstruction, 2013.

Figures

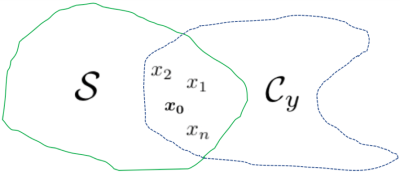
Admissible reconstructions ($$$x_0$$$ is the true image).

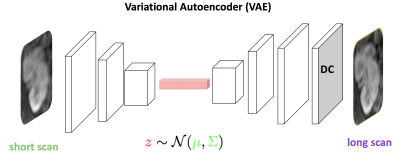
The model architecture, with aliased input images feeding into the VAE encoder, the latent code feeding into the VAE decoder, and data consistency applied to obtain the output reconstruction. This output serves as an input to the GAN discriminator, which in turn sends feedback to the generator.

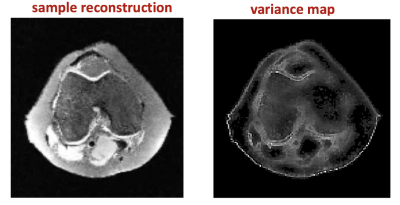
A sample reconstruction and variance map based on 1K reconstructions using 5-fold undersampling with 5% GAN loss.

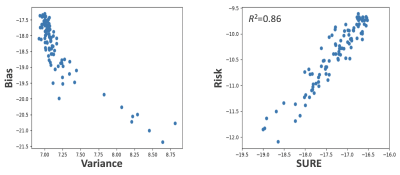
Bias vs. variance and MSE vs. SURE log-log plots for test images with 5-fold undersampling and 5% GAN loss.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3599