3595
Exploiting Coarse-Scale Image Features for Transfer Learning in Accelerated Magnetic Resonance Imaging1Department of Radiology, Stanford University, Stanford, CA, United States, 2Department of Electrical Engineering, Stanford University, Stanford, CA, United States
Synopsis
This work investigates coarse-scale image features for transfer learning in accelerated magnetic resonance imaging. The model uses multi-scale unrolled CNN architecture that captures image features at coarse and fine scale to efficiently reduce the training sample size for deep learning model training.
Introduction
Model-based and Data-centric deep learning (DL) based models have shown promising results in accelerating Magnetic Resonance Imaging (MRI)[1,2, 4,8]. However, DL architectures demand sufficient training data to learn the mapping function from undersampled aliased images to desired high-resolution images. This makes DL frameworks infeasible in cases where such high-resolution training data are not abundantly available. In this abstract, we present a new framework that exploits the low-level image features to substantially decrease the training data size for accelerated MRI.Methods
Our framework is motivated by two fundamental principles: i) In the image domain, several images have common coarse-level image features such as smoothness, contrast, structures, and ii) most of the energy of MR images are often concentrated around low-frequency components of the k-space (around center k-space).Deep Learning Model: To exploit these two principles and learn image features at two different scales coarse-scale and fine-scale corresponding to low frequency and high-frequency components of k-space we developed a multi-scale CNN-based unrolled DL framework as shown in Fig.1. Multi-scale DL architecture consists of two deep learning blocks Coarse-scale and Fine-scale blocks for which the inputs are correspondingly low-pass filtered and high-pass filtered images. We use a Gaussian kernel filter to minimize Gibb’s ringing. Each DL block consists of two ResNet [5] blocks which are made using two convolution layers and a relu activation unit as shown in Fig. 2. Outputs of each DL block are combined through a single CNN layer as shown in Fig. 1. Data consistency and coil sensitivity information are incorporated using unrolled architecture as described in [6,7,8,9]. Weighed $$$\ell_2$$$ loss is computed in the k-space such that $$$\cal{L}(k,\hat{k})=\omega_l* ||k_l-\hat{k}_l|| +(1-\omega_l)* ||k_h-\hat{k}_h||$$$, where $$$ k_l,\;k_h,\;\hat{k}_l\;and\;\hat{k}_h $$$, are low frequency and high-frequency k-space components of estimated and reference k-space corresponding to the low pass and high pass filters outputs, $$$\omega_l >0.5$$$ is a weighting factor which weights the low-frequency components heavily than the high-frequency components.
Implementation, Training Dataset and Transfer Learning: We implemented our framework in TensorFlow 1.10.1. Adam optimizer with β1 = 0.99, β2 = 0.99, learning rate α = 0.001 is used. Weight factor of $$$\omega_l=0.6$$$ was chosen during the training phase. Coarse scale DLN consists of F = 64 convolution kernel filters of size k1 = 8 × 8 at each convolution layer whereas, fine-scale DLN consists of F = 64 convolution kernel filters of size k2 = 2 × 2 at each convolution layer. For the unrolled network, Q = 2 numbers of proximal iterations were carried out. Training Data: The model was trained on the knee MRI dataset. The raw data were 32 coils, 3D volume data. The data was converted into 2 D image data by taking an inverse Fourier Transformation along the z-direction and coil compressed using [3]. As a result, 6400, 8-coil axial view knee MR images were obtained. The training data images were divided into 60-15-25% train, validation, and test sets, respectively. For training purposes, a total of 35, 2D variable density undersampling masks with different undersampling rates of 2, 3, 4, 6, and 9 were used. Investigating Transferability of the Model: To test the transferability of the model, we use two datasets. i) Coronal view knee images and ii) body MR images. In the case of coronal view reconstruction, we use the model trained in the axial view knee images directly and reconstruct (make inference directly) without any further training and new data. In the case of body MR images, we carry out two experiments. First out of ~5200 MR images from various anatomical regions, the data is divided into 60-15-25% train, validation, and test sets, respectively and the DL model is trained from scratch (Figure 4,5, case-a). In the second experiment, we infer reconstructions of undersampled test images using the model trained from scratch using only 1/3rd of training data (Figure 4,5, case-c), and from the model initialized with weights learned using axial knee image training dataset and further trained on 1/3rd of body image training data set (Figure 4,5,case-b) for 20,000 further iterations.
Results and Discussions
Figure 3 shows reconstruction results of coronal view knee images at undersampling rates of 6 and 9 using the single-scale unrolled network[8,7] and multi-scale unroll network[8] trained on axial view knee images. We can see that the reconstruction results from the multi-scale network are much cleaner and have lower RNMSE values confirming that the multi-scale network has better transferability for multi-view reconstruction. This is possible because the multi-scale network is able to capture smoothness of images more efficiently due to higher priority given to the coarse-scale image features. Figure 4 shows the reconstruction results for body MR test images at a reduction factor of 4. Figure 5 shows RNMSE values for two different test cases at different reduction factors. In both cases, we can see that the multi-scale network has a better transferability. In the case of body MR images, we can see that by transferring weights, the multi-scale network is able to achieve similar performance using only 1/3rd of training data.Conclusion
We investigated the transferability of multi-scale unrolled CNN architecture which is capable of learning corse scale image features.Acknowledgements
This work is supported in part by the NIH R01EB009690, NIH R01 EB026136 grants, and GE Healthcare.References
- Z.-P. Liang and P. C. Lauterbur, “An efficient method for dynamic magnetic resonance imaging,” Medical Imaging, IEEE Transactions on, vol. 13, no. 4, pp. 677–686, 1994.
- M. Lustig, D. Donoho, and J. M. Pauly, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magnetic Resonance in Medicine, vol. 58, no. 6, pp. 1182–1195, 2007.
- T. Zhang, J. M. Pauly, S. S. Vasanawala, and M. Lustig, “Coil compression for accelerated imaging with cartesian sampling,” Magnetic Resonance in Medicine, vol. 69, no. 2, pp. 571–582, 2013.
- S. Wang, Z. Su, L. Ying, X. Peng, S. Zhu, F. Liang, D. Feng, and D. Liang, “Accelerating magnetic resonance imaging via deep learning,” in 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), April 2016, pp. 514–517.
- K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” CoRR, vol. abs/1512.03385, 2015.
- S. Diamond, V. Sitzmann, F. Heide, and G. Wetzstein, “Unrolled optimization with deep priors,” CoRR, vol. abs/1705.08041, 2017.
- U. Nakarmi, J. Y. Cheng, et.al., "Multi-scale Unrolled Deep Learning Network for Accelerated MRI", ISMRM 2019, Montreal, QC, Canada.
- J. Y. Cheng, F. Chen, M. T. Alley, J. M. Pauly, and S. S. Vasanawala, “Highly scalable image reconstruction using deep neural networks with bandpass filtering,” CoRR, vol. abs/1805.03300, 2018.
- A. Beck and M. Teboulle, “A fast iterative shrinkage-thresholding algorithm for linear inverse problems,” SIAM Journal on Imaging Sciences, vol. 2, no. 1, pp. 183–202, 2009.
Figures
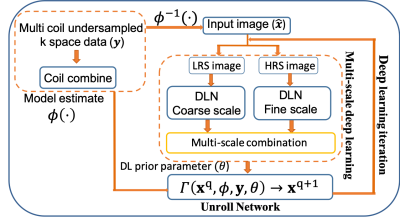
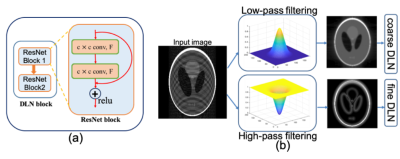
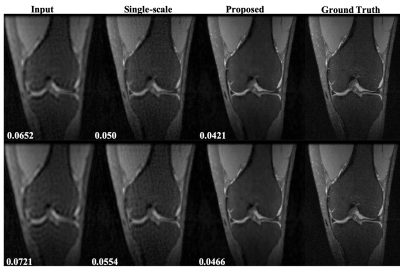
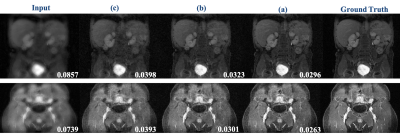
Figure 4. Representative results for body MR image reconstruction using transfer learning at a reduction factor = 4. (a) Reconstruction from the model trained on body image training dataset. (b) Reconstruction from a model trained using transfer learning from a model trained on axial knee images and 1/3rd of the body image training dataset. c) Reconstruction from a model trained using only 1/3rd of the body image training dataset. The numbers on the bottom right represent RNMSE values.
