3592

A Further Analysis of Deep Instability in Image Reconstruction

Yue Guan¹, Yudu Li^2,3, Yao Li¹, Yiping Du¹, and Zhi-Pei Liang^2,3
¹Institute for Medical Imaging Technology, School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, ²Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, ³Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States

Synopsis

Deep learning (DL) has emerged as a new tool for solving ill-posed image reconstruction problems and generated a lot of interest in the MRI community. However, image learning is a very high-dimensional problem and deep networks, if not trained properly, would have instability problems. Building upon a recent analysis, we present a further analysis of the instability problems, highlighting: a) the overfitting problem due to limited training data, b) inaccurate density estimation, and c) inadequate sampling from a probability density function. We also present a theoretical analysis of the prediction error based on statistical learning theory.

Introduction

Deep learning (DL) has emerged as a new tool for image reconstruction and generated much interest in the MRI community. General approaches to DL-based reconstruction include: a) direct methods that learn the nonlinear transformation from measured data to the desired images and use the network output as the final reconstruction ^1,2,and b) indirect methods that learn the image priors embedded in the training data and then incorporate them via regularization for the final reconstruction ^3,4.In either approach, image learning is a very high-dimensional problem and huge amounts of training data are often required to train the network properly, otherwise, instability problems would occur ⁵. Building on a recent analysis⁵,we present a further study of the instability problem, highlighting the following sources of instable reconstructions: a) overfitting, b) inaccurate density estimation, and c) inadequate sampling. We also present a theoretical analysis of the prediction error based on statistical learning theory.

Illustration of Deep Instabilities in Image Reconstruction

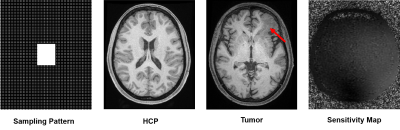
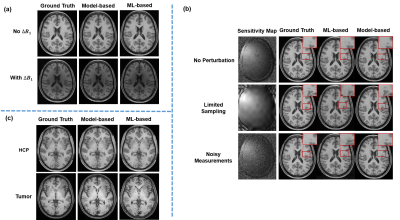
To illustrate the instability problem, we performed image reconstruction from sparsely sampled MPRAGE data, which often used to test DL-based reconstruction methods. More specifically, we retrospectively sampled the MPRAGE data using a dual-density sampling pattern (Fig. 1a). We used the large datasets from the Human Connectome Project (HCP) for training ⁶(Fig. 1b) and used a new tumor data for testing (Fig. 1c). To generate multichannel data, we obtained a set of 20-channel sensitivity functions (Fig. 1d) from a healthy subject using a FLASH sequence and co-registered and applied them to all the MPRAGE images.

Different scenarios were considered to mimic the instability problems encountered in practice: (1) The newly acquired imaging data has low-order intensity discrepancies to the training data, caused by B1 inhomogeneity; (2) The sensitivity profiles used in image reconstruction has been perturbed due to limited sampling or presence of noise; (3) The imaging data containing novel features is not seen in the training data, e.g., the lesions in our tumor data. In each scenario, we used the state-of-the-art network structure DAGAN⁷to learn the image priors from the HCP database. As a reference, we also performed the traditional model-based image reconstruction, incorporating a subspace structure learnt from the same MPRAGE training images.The reconstruction results are shown in Fig. 2. As can be seen, the DL-based reconstructions were much more sensitive to “perturbations” than the conventional model-based method and produced significant image artifacts.

Potential Sources of Deep Instabilities

Overfitting: Image learning is a very high-dimensional problem and often requires large amounts of data to properly train the large number of parameters in a deep network. For example, a typical 2D MR image has about $$$256\times 256\approx 6.5\times10^4$$$ degrees-of-freedom and typical network architectures can have millions of parameters. Insufficient training samples can result in overfitting. To illustrate this problem, we trained a three-layer perceptron model to learn an order-3 polynomial. Figure 3 shows the accuracy of the learned polynomial highly depends on the training data size.

Inaccurate Estimation of the Prior Distributions: Image intensity distributions are non-Gaussian and often highly complex. While deep networks can function as universal approximators in theory, gradient descent-based training procedures can get trapped in a saddle point, leading to inaccurate estimation of the image distributions even with sufficient data. A typical example is the well-known “modal collapse” problem associated with GAN, which has been recently proved to be related to convergence to a local equilibrium in a non-convex game⁸. Figure 4 illustrates “modal collapse” in training the MNIST data.

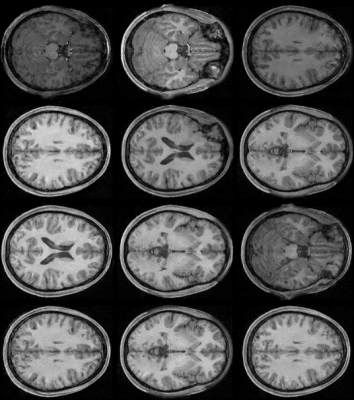
Inadequate Sampling: Even with an accurate image distribution, how to effectively sample it to generate the desired reconstruction still remains a practical issue because of the high dimensionality of image distributions ($$$\sim 10^4$$$). In practice, the samples drawn from the learned distribution may have significant variations, as illustrated in Fig. 5. Therefore, a carefully designed sampling strategy is needed for stable reconstructions.

Bounds on Generalization Errors

There are no tight theoretical bounds yet on generalization/reconstruction errors associated with DL-based reconstruction methods. Some established results in statistical learning theory can be used to characterize the sample complexity (i.e., number of training samples required to achieve desirable accuracy), which may provide some useful insights. To this end, the accuracy (i.e., generalization error) of a neural network trained under empirical risk minimization (ERM) principle is bounded by:
$$L(f) \leq \frac{4}{n}\prod^d_{j=1}M_F(j)(\sqrt{2\log(2)d}+1)\sqrt{\sum^m_{i=1}\Vert x_i\Vert^2}+\sqrt{\frac{2\log\frac{1}{\delta}}{n}}$$
with confidence level $$$1-\delta$$$ for $$$n$$$ training samples⁹. $$$d$$$ denotes the number of layers, $$$M_F(j)$$$ norm of parameters in each layer and $$$x_i$$$ the input samples. Eq. (1) suggests that the sample complexity of a neural network grows polynomially with $$$d$$$. Given the neural networks used in practice often have deep architectures, large number of training data would be crucial to achieve a reasonable learning performance and avoid the overfitting issue, consistent to our results.

Conclusions

Image learning is a very high-dimensional problem; it requires huge amounts of training data that are often well beyond what are currently available. As a result, significant image artifacts can result due to: a) overfitting, b) inaccurate estimation of prior distributions (e.g., mold collapse), and c) inadequate sampling from a learnt prior distribution.This paper provides a systematic analysis of these issues, which may provide useful insights into developing robust specialized DL-based methods for solving specific image reconstruction problems.

Acknowledgements

No acknowledgement found.

References

1. Mardani M, Gong E, et al. Deep generative adversarial neural tetworks for compressive sensing MRI. IEEE Trans Med Imaging. 2019;38(1):167-179.2

2. Zhu B, Liu JZ, Cauley SF, et al. Image reconstruction by domain-transform manifold learning. Nature, 2018;555(7697):487-492.3

3. Wang S, et al. Accelerating magnetic resonance imaging via deep learning. 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI). IEEE, 2016; 514-517.4

4. Schlemper J, Caballero J, Hajnal JV, et al. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Trans Med Imaging, 2017; 37(2):491-503.5

5. Antun V, Renna F, Poon C, et al. On instabilities of deep learning in image reconstruction-Does AI come at a cost? arXiv preprint arXiv, 2019.6

6. Van Essen DC, Smith SM, Barch DM, et al. The WU-Minn Human Connectome Project: an overview. Neuroimage. 2013;80:62–79.7

7.Yang G, Yu S, Dong H, et al. DAGAN: deep de-aliasing generative adversarial networks for fast compressed sensing MRI reconstruction. IEEE Trans Med Imaging, 2017, 37(6): 1310-1321.

8. Kodali N, Abernethy J, Hays J & Kira Z. On convergence and stability of gans. arXiv preprint arXiv, 2017.8

9. Golowich N, Rakhlin A. & Shamir O. Size-independent sample complexity of neural networks. arXiv preprint arXiv, 2017.

Figures

Figure 1: (a) k-space sampling pattern: the central k-space (36 x 42) was fully sampled and outer k-space was undersampled with R = 3 in both phase encoding directions. (b) Representative MPRAGE images from the HCP database. (c) Newly acquired MPRAGE images from a tumor patient. (d) Sensitivity maps obtained from FLASH images.

Figure 2: Illustration of deep instabilities in image reconstruction in presence of: (a) Low-order intensity discrepancies due to B1 inhomogeneity; (b) Perturbation of sensitivity maps due to limited sampling and noise; (c) Subject-dependent novel features such as tumors. In each scenario, we compared the DL-based reconstruction to the model-based reconstruction exploiting the low-rank structures. As can be seen, the DL-based reconstructions were much more sensitive to “perturbations” to the data, as compared to the conventional method.

Figure 3: Illustration of the overfitting problem in DL. In this experiment, we trained a three-layer perceptron model to learn an order-3 polynomial function, with number of training samples being (a) N = 5, (b) N = 10, (c) N = 50, and (d) N=100. We also reported the L1 and L2 loss in different cases as shown in the table. As can be seen, the accuracy of the learned polynomial highly depends on the training data size.

Figure 4: Illustration of the well-known “modal collapse” problem associated with GAN. In this experiment, we learned the distribution embedded in the MNIST datasets using GAN. As can be seen, the generated samples almost all collapsed to digit “1”.

Figure 5: Illustration of the inadequate sampling issue. The images shown were generated from a deep generative model (DCGAN) trained using the the HCP database. As can be seen, the generated reconstruction samples have large variations, which would lead to unstable reconstructions if they were used directly as the final reconstruction or indirectly as a prior. For more stable reconstructions, a carefully designed sampling strategy would be needed to obtain sampled reconstructions from a learned distribution (or deep generator).

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3592