3591

Hybrid Deep Neural Network Architectures for Multi-Coil MR Image Reconstruction
Salman Ul Hassan Dar1,2, Mahmut Yurt1,2, Muzaffer Özbey1,2, and Tolga Çukur1,2,3
1Department of Electrical and Electronics Engineering, Bilkent University, Ankara, Turkey, 2National Magnetic Resonance Research Center (UMRAM), Bilkent University, Ankara, Turkey, 3Neuroscience Program, Aysel Sabuncu Brain Research Center, Bilkent University, Ankara, Turkey

Synopsis

Two main frameworks for reconstruction of undersampled MR acquisitions are compressive sensing/parallel imaging methods (CS-PI) and deep neural networks (DNNs). CS-PI relies on sparsity in fixed transform domains and requires careful hyperparameter tuning. On the other hand, DNNs for multi-coil reconstructions can be difficult to train due to increased model complexity. To address these limitations, we propose a DNN-PI hybrid in which DNNs that learn population-driven priors are combined with PI that learns subject-specific priors. Evaluations on T1/T2-weighted brain images demonstrate the improved immunity of DNN-PI to scarce training data and suboptimal hyperparameter selection.

Introduction

Two mainstream frameworks for recovery of undersampled MR acquisitions are compressive sensing-parallel imaging (CS-PI)1–3, and deep neural networks (DNNs)4–10. CS-PI weighs subject-specific priors learned based on a physical signal model against fixed sparsity priors in a priori known transform domains. Suboptimality of the sparsifying transform domain and poor hyperparameter selection can thereby limit reconstruction performance. In contrast, DNNs perform end-to-end recovery of undersampled acquisitions by learning population-driven priors from large training datasets4–10. While DNNs do not assume transform domains, training DNNs for multi-coil reconstructions can prove difficult due to increased model complexity, especially when training data are scarce. To address these limitations, here we propose a hybrid DNN-PI (Hybrid-DNN) architecture11 that complementarily merges population-driven priors in DNNs with subject-driven priors in PI.

Methods

Reconstruction of under-sampled acquisitions with Hybrid-DNN can be formulated as follows:$$x_{rec} =\min_{x} \parallel F_{u}x-y_{u} \parallel_{2}+ \parallel (G-I)Fx \parallel_{2} + \parallel C(A^{*}x_{u};\theta^{*})-A^{*}x \parallel_{2} \; (1)$$In Eq. 1, the first term enforces consistency with the acquired data where $$$x$$$ is the image to be reconstructed, $$$F_{u}$$$ is the Fourier transform operator at acquired k-space locations, and $$$y_{u}$$$ are the acquired k-space data. The second term enforces consistency with the calibration data where $$$G$$$ is the interpolation operator based on SPIRiT2 that synthesizes missing k-space samples from acquired samples. The third term enforces consistency with the DNN reconstruction where $$$C$$$ is the output of a trained network with parameters $$$\theta^{*}$$$, $$$A$$$ and $$$A^{*}$$$ denote coil sensitivity maps and their adjoints obtained via ESPIRiT12. Note that the DNN is trained off-line to recover fully-sampled coil-combined images given undersampled coil-combined images. Eq. 1 can be solved by performing alternating projections for data-consistency (DC), calibration-consistency (CC) and DNN-consistency (DNNC) blocks.

Hybrid-DNN was implemented via an unrolled cascade of 5 subnetworks5, where each subnetwork consisted of DNNC blocks interleaved with DC and CC blocks (Fig. 1). The DNNC block within each subnetwork contained 3 hidden layers and 64 3x3 convolution kernels within each layer. Each DNNC block was initially trained separately for 20 epochs with a learning rate of $$$\eta$$$=10-4, followed by an end-to-end tuning of the entire network for 100 epochs with $$$\eta$$$=10-5. Network weights were L2-regularized with a parameter of 10-6. The Adam optimizer13 was used with parameters $$$\beta_{1}$$$=0.9 and $$$\beta_{2}$$$=0.999. For the CC block, SPIRiT2 was used with an interpolation kernel of size 7 estimated from a calibration region of size 30x30. To examine sensitivity to the Tikhonov parameter ($$$\lambda$$$) used in estimation of the interpolation kernel, several networks were trained based on interpolation kernels for $$$\lambda$$$ in [10-3,10-1].

Demonstrations were performed on multi-coil T1- and T2-weighted complex brain images of 10 subjects (6 reserved for training, 1 for validation, 3 for testing) collected on a 3T Siemens Tim Trio scanner equipped with a 32-channel head coil. The images were acquired with a matrix size=256x192x80 and resolution=1x1x2mm3. For all analyses, 60 axial cross-sections within each subject that contained brain tissue were selected. To reduce computational complexity, data were compressed from 32 to 8 coils using geometric coil compression14. Retrospective undersampling was performed via the Poisson-disc method for acceleration factors R=4-102. Hybrid-DNN was compared against DNN and L1-SPIRiT. The training procedures for DNN were identical to Hybrid-DNN. All hyperparameters in L1-SPIRiT were optimized via cross-validation, except for the convergence criterion (convergence was taken as the iteration where absolute difference in reconstructed images between consecutive iterations fell below 10-5).

Results

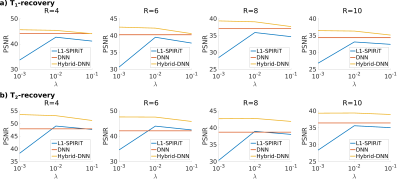
Table 1 lists average PSNR (peak SNR) measurements of recovered T1- and T2-weighted images from test subjects at R=4-10. On average across R, Hybrid-DNN achieves 1.80dB higher PSNR in T1-weighted image recovery and 3.61dB higher PSNR in T2-weighted image recovery as compared to the second-best performing method.

Figure 2 displays PSNR across the test subjects as a function of Tikhonov parameters $$$\lambda$$$=[10-3,10-1] that are used for estimating interpolation kernel in SPIRiT. Note that a properly-tuned L1-SPIRiT can outperform DNN in many cases, likely due to the relative scarcity of training data. While L1-SPIRiT shows substantial sensitivity to $$$\lambda$$$, Hybrid-DNN yields consistently high PSNR values for varying $$$\lambda$$$.

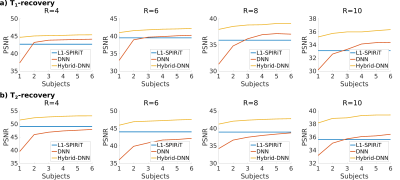
Figure 3 shows PSNR measurements across the test subjects as a function of number of training subjects used for training DNN and Hybrid-DNN models, along with measurements for L1-SPIRiT (properly-tuned). DNN requires nearly 3 subjects in T1 and 6 subjects in T2 recovery to achieve a performance level comparable to L1-SPIRiT. In contrast, Hybrid-DNN achieves higher performance compared to L1-SPIRiT even when a single subject is used for training.

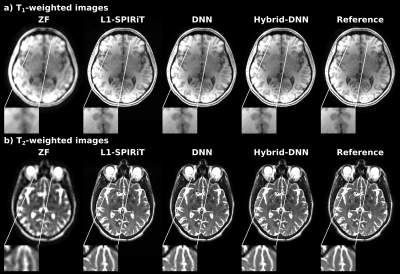
Figure 4 displays representative T1- and T2-weighted reconstructions from L1-SPIRiT, DNN and Hybrid-DNN at R=8, where Hybrid-DNN and DNN were trained on a single subject. Hybrid-DNN yields more accurate depictions in many regions where the competing methods suffer from visible reconstruction artifacts.

Discussion

Here we demonstrated a hybrid architecture to recover undersampled MR acquisitions. The proposed architecture enhances the immunity of the DNN component to scarcity of training data, while improving the resilience of the PI component to suboptimal hyperparameter selection.

Conclusion

The proposed approach enables improved recovery of missing data in undersampled MR acquisitions by efficiently weighing a population-driven prior against a subject-driven prior in multi-coil reconstructions.

Acknowledgements

This work was supported in part by a Marie Curie Actions Career Integration Grant (PCIG13- GA-2013-618101), by a European Molecular Biology Organization Installation Grant (IG 3028), by a TUBA GEBIP fellowship, by a TUBITAK 1001 Grant (118E256), and by a BAGEP fellowship awarded to T. Çukur. We also gratefully acknowledge the support of NVIDIA Corporation with the donation of the Titan X Pascal GPU used for this research.

References

1. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007;58:1182–1195 doi: 10.1002/mrm.21391.

2. Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn. Reson. Med. 2010;64:457–71 doi: 10.1002/mrm.22428.

3. Lustig M, Donoho DL, Santos JM, Pauly JM. Compressed Sensing MRI. IEEE Signal Process. Mag. 2008;25:72–82 doi: 10.1109/MSP.2007.914728.

4. Hammernik K, Klatzer T, Kobler E, et al. Learning a Variational Network for Reconstruction of Accelerated MRI Data. Magn. Reson. Med. 2017;79:3055–3071.

5. Schlemper J, Caballero J, Hajnal J V., Price A, Rueckert D. A Deep Cascade of Convolutional Neural Networks for MR Image Reconstruction. In: International Conference on Information Processing in Medical Imaging. ; 2017. pp. 647–658.

6. Mardani M, Gong E, Cheng JY, et al. Deep Generative Adversarial Neural Networks for Compressive Sensing (GANCS) MRI. IEEE Trans. Med. Imaging 2018:1–1 doi: 10.1109/TMI.2018.2858752.

7. Han Y, Yoo J, Kim HH, Shin HJ, Sung K, Ye JC. Deep learning with domain adaptation for accelerated projection-reconstruction MR. Magn. Reson. Med. 2018;80:1189–1205 doi: 10.1002/mrm.27106.

8. Wang S, Su Z, Ying L, et al. Accelerating magnetic resonance imaging via deep learning. In: IEEE 13th International Symposium on Biomedical Imaging (ISBI). ; 2016. pp. 514–517. doi: 10.1109/ISBI.2016.7493320.

9. Yu S, Dong H, Yang G, et al. DAGAN: Deep de-aliasing generative adversarial networks for fast compressed sensing MRI reconstruction. IEEE Trans. Med. Imaging 2018;37:1310–1321.

10. Zhu B, Liu JZ, Rosen BR, Rosen MS. Image reconstruction by domain transform manifold learning. Nature 2018;555:487–492 doi: 10.1017/CCOL052182303X.002.

11. Dar SUH, Özbey M, Çatlı AB, Çukur T. A Transfer-Learning Approach for Accelerated MRI using Deep Neural Networks. arXiv Prepr. 2017.

12. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014;71:990–1001 doi: 10.1002/mrm.24751.

13. Kingma DP, Ba JL. Adam: a Method for Stochastic Optimization. In: International Conference on Learning Representations. ; 2015. doi: http://doi.acm.org.ezproxy.lib.ucf.edu/10.1145/1830483.1830503.

14. Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn. Reson. Med. 2013;69:571–82 doi: 10.1002/mrm.24267..


Figures

Figure 1. (a) The hybrid architecture consists of multiple subnetworks where each subnetwork contains deep neural network-consistency (DNNC) and calibration-consistency (CC) blocks, both followed by a data-consistency (DC) block. (b) Each DNNC block contains two networks that reconstruct real and imaginary parts of the coil-combined images that are then projected back onto individual coils using coil sensitivity maps A. (c) Each CC block applies interpolation operator G in the Fourier domain.

Figure 2. Average PSNR values across (a) T1- and (b) T2-weighted brain images of 3 test subjects as a function of Tikhonov parameters (λ) used for the estimation of interpolation kernel. Results are shown for R=4-10. Both DNN and Hybrid-DNN were trained on 6 subjects. Unlike L1-SPIRiT, Hybrid-DNN achieves consistently high PSNR values for varying λ. Furthermore, it outperforms both DNN and L1-SPIRiT.

Figure 3. Average PSNR values across (a) T1- and (b) T2-weighted images of 3 test subjects as a function of number of training subjects. Results are shown for R=4-10. Hybrid-DNN outperforms L1-SPIRiT even when the network is trained on a single subject. On the other hand, DNN requires nearly 3 subjects in T1 and 6 subjects in T2 recovery to achieve a performance level comparable to L1-SPIRiT.

Figure 4. Representative reconstructions of (a) T1- and (b) T2-weighted images via L1-SPIRiT, DNN and Hybrid-DNN at R=8 are displayed. Hybrid-DNN and DNN were trained on a single subject. Hybrid-DNN outperforms both DNN and L1-SPIRiT in terms of residual artifacts.

Table 1. Reconstruction quality for T1- and T2-weighted images undersampled at various acceleration factors (R=4-10). Both Hybrid-DNN and DNN were trained on 6 subjects. PSNR measurements are listed as mean±standard deviation across images from 3 test subjects. Top performing models are marked with boldface.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
3591