3587
Joint Optimization of Sampling Patterns and Deep Priors for Improved Parallel MRI1Electrical and Computer Engineering, University of Iowa, Iowa City, IA, United States
Synopsis
Model-based deep learning (MoDL) frameworks, which combine deep learned priors with imaging physics, are now emerging as powerful alternatives to compressed sensing in a variety of reconstruction problems. In this work, we investigate the impact of sampling patterns on the image quality. We introduce a scheme to jointly optimize the sampling pattern and the reconstruction network parameters in MoDL scheme. Experimental results demonstrate the significant improvement in reconstruction quality with sampling optimization. The results also show that the decoupling between imaging physics and image properties in MoDL offers improved performance over direct inversion scheme in the joint optimization scheme.
Introduction
Modern MRI schemes rely on parallel imaging hardware to accelerate the acquisition. Parallel MRI widely utilize regularization algorithms that exploit various image properties (e.g., sparsity, low-rank). Recently, model-based deep learning algorithms that combine the imaging physics along with deep-learned priors are being increasingly used, with significantly improved performance over compressed sensing algorithms. The image quality depends on the specific deep priors, that can be learned from exemplary images, as well as the sampling pattern, but is not well-studied.The main focus of this work is to jointly optimize the sampling pattern and the deep prior in a MoDL framework with application to parallel MRI. The joint optimization strategy is expected to provide improved performance compared to the classical pseudo-random patterns. We study the utility of the proposed strategy with both direct inversion [1] and model-based methods [3]. The strong coupling between CNN parameters and the specific sampling pattern in the direct-inversion schemes [1] makes their joint optimization challenging. By contrast, model-based schemes use the information of the sampling pattern within the reconstruction algorithm, thus decoupling the CNN block from changes in sampling pattern. This improved decoupling between the parameters in model-based approaches is expected to offer improved performance.
Proposed Method
The model-based deep learning frameworks formulate the reconstruction process as a regularized inverse problem where a deep neural network is used as prior. We propose to formulate the joint recovery as$$\hat{\mathbf x}_{\{\boldsymbol \Theta,\Phi\}}= \text{arg}\min_{\mathbf x} \|\mathbf b-\mathcal A_ {\boldsymbol \Theta}(\mathbf x) \|_2^2 + ~ \|\mathbf x - \mathcal D_{\Phi}(\mathbf x)\|_F^2, (1)$$
Where, the forward operator $$$\mathcal A_\Theta$$$ is implemented as a 1-D discrete Fourier transform to map the spatial locations to the continuous domain Fourier samples specified by $$$\Theta$$$, following the weighting by the coil sensitivities. $$$\mathcal D_{\Phi}$$$ is residual learning based convolutional neural network with parameter $$$\Phi$$$ that is designed to extract the noise and alias terms in $$$\mathbf x$$$. The notation $$$ \hat{\mathbf x}_{\{\boldsymbol \Theta,\Phi\}}$$$ denotes the dependence of the solution $$$\mathbf x$$$ on the sampling pattern $$$\Theta$$$ as well as regularization parameters $$$\Phi$$$.
Figure. 1 shows the proposed joint model-based deep learning framework (J-MoDL), where we simultaneously optimize for the sampling pattern $$$\Theta$$$ as well as the network parameters $$$\Phi$$$.
The network in Fig. 1 was unrolled for K=5 iterations i.e., five iterations of alternating minimization were used to solve Eq. (1). The data-consistency block $$$\mathcal Q_\Theta$$$ is implemented using conjugate gradients algorithm. The CNN block $$$\mathcal D_\Phi$$$ is implemented as a UNET with four pooling and unpoolong layers. The parameters of the blocks $$$\mathcal D_\Phi$$$ and $$$\mathcal Q_\Theta$$$ are optimized to minimize the training loss
$$\{\boldsymbol \Theta^*,\Phi^*\} = \text{arg}\min_{\boldsymbol \Theta ,\Phi} \sum_{i=1}^{N} \| \mathcal M_{\boldsymbol \Theta,\Phi} \left(\mathcal A_{\boldsymbol \Theta}(\mathbf x_i)\right) -\mathbf x_i \|_2^2, (2)$$
where, $$$\mathcal M_{\Theta,\Phi}$$$ is the joint network that simultaneously learns the sampling as well as the network parameters.
Results
Experiments utilized two publically available, brain and knee, parallel MRI datasets2,3.Figure 2 visually demonstrates the benefit of joint optimization in the model-based framework as compared to joint optimization in the direct-inversion based method (UNET) at six-fold acceleration. The joint-learning of sampling and UNET parameters is referred to as the J-UNET approach. The utilization of the data-consistency step in a model-based framework helps to reduce the blurring, better preserving the high-frequency details, and reduces hallucination as pointed by arrows in the zoomed area. Similarly, Fig. 3 compares J-UNET and proposed J-MoDL at ten-fold acceleration on the brain dataset with an optimized 2D sampling mask and network.
Figure 4 shows that an optimized sampling pattern results in improved re-gridding reconstruction that helps in further improving the reconstruction quality in the MoDL framework. Figure 4 shows the results of three different training strategies. First, $$$\Phi$$$ alone means only the reconstruction network is optimized keeping fixed sampling masks. Second, $$$\Theta$$$ alone refers to the case where only the sampling mask is optimized while the reconstruction network is kept fixed. Third, $$$\Theta, \Phi$$$ joint refers when both mask, as well as network parameters, are optimized jointly. It can be noted that the optimized mask reduces the aliasing from $$$\mathcal A^Hb$$$ as compared to a fixed mask.
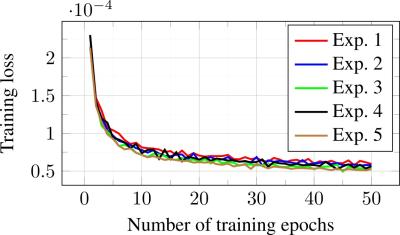
The plot in Fig. 5 shows that unrolled J-MoDL training proceeds relatively smooth despite the problem formulation (1) being highly non-convex. Initially, we trained a MoDL architecture with incoherent sampling patterns. These trained network parameters were used as an initialization for the five independent J-MoDL training processes. Each of the five J-MoDL architectures was initialized with different random sampling masks and trained for 50 epochs. It is observed that all five models converge to nearly the same local minima values.
Conclusions
This work proposed a model-based deep learning framework to optimize for both the sampling and the reconstruction network parameters jointly for parallel MRI. Experimental results demonstrated the benefits of optimizing the sampling pattern in the proposed model-based framework. The proposed J-MoDL architecture provides better decoupling between the sampling and reconstruction network parameters. This decoupling makes the reconstruction network more robust to changes in sampling patterns as compared to joint reconstruction in the direct-inversion based techniques.Acknowledgements
This work is supported by 1R01EB01996101A1. This work was conducted on an MRI instrument funded by 1S10OD025025-01.References
- Yoseob Han, Leonard Sunwoo, and Jong Chul Ye, “k-space deep learning for accelerated MRI,” IEEE Trans.Med. Imag., 2019
- Kerstin Hammernik et. al., “Learning a Variational Network for Reconstruction of Accelerated MRI Data,” Magnetic Resonance in Medicine, vol. 79, no. 6, pp. 3055–3071,2017.
- Hemant K Aggarwal, Merry P Mani, and Mathews Jacob, “MoDL: Model-based deep learning architecture for inverse problems,” IEEE Trans. Med. Imag., vol. 38,no. 2, pp. 394–405, 2019
Figures
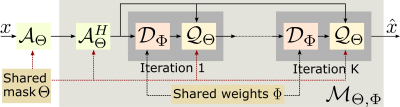
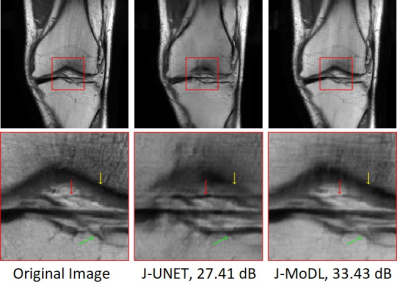
Fig. 2: 1D case: Comparison of joint learning in direct-inversion (J-UNET) and model-based deep learning (J-MoDL) frameworks. A six-fold undersampling was performed in the phase-encoding direction while having fully sampled frequency encodes. Yellow arrows are pointing to a feature that is blurred in the J-UNET whereas J-MoDL correctly retains it. Red arrows point to a feature in-correctly sharpened by the J-UNET. Green arrows are pointing to a feature completely missed by the J-UNET.
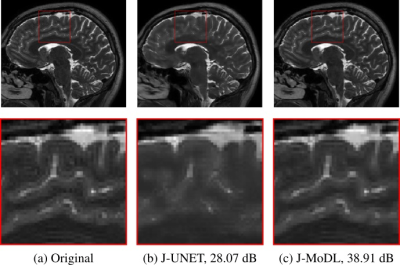
Fig. 3: 2D case: Comparison of joint learning in direct-inversion (J-UNET) and model-based deep learning (J-MoDL) frameworks. Undersampling is performed in both frequency and phase encoding directions to achieve ten-fold acceleration. The zoomed area clearly shows that the proposed J-MoDL reconstruction quality is better than J-UNET.
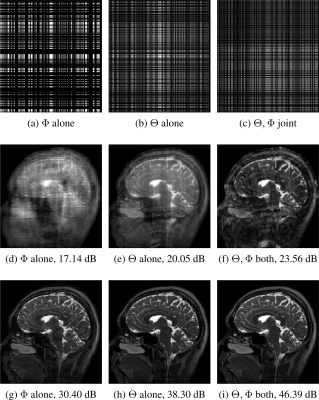
Fig. 4: Row 1, row 2, and row 3 show masks, re-gridding reconstruction, and network outputs respectively. $$$\Theta$$$ and $$$\Phi$$$ refers to sampling and reconstruction network parameters, respectively. The results are shown at a six-fold acceleration case. The numbers in the sub-captions show the PSNR values.