3586

Deep Dixon: Deep learning-based chemical-shift corrected water-fat separation with only simulated training data

Frank Zijlstra¹ and Peter R Seevinck¹
¹Image Sciences Institute, UMC Utrecht, Utrecht, Netherlands

Synopsis

Deep learning has been successfully applied to Dixon reconstruction, but requires good training data, which limits clinical applicability. We propose a deep learning-based Dixon method with chemical-shift correction that is trained with only simulated data. Results on three anatomies show that the method produces equivalent or better results than conventional methods for Dixon water-fat separation with chemical-shift correction. This approach is fundamentally different from conventional linear and non-linear solvers and shows promise for extension to more complex problems.

Introduction

Dixon water-fat separation is a commonly applied post-processing step to separate water and fat signals from multi-echo acquisitions¹. Over the years, the original Dixon method has been extended, for example to include T₂^*-mapping² and to correct for chemical-shift in acquisitions with bipolar readouts³. Developing such methods requires a good understanding of the underlying physics and how to solve inverse problems using linear and non-linear solvers.

As an alternative to conventional methods, deep learning-based Dixon methods have been applied with very good results^4,5, even on single-echo acquisitions where conventional Dixon methods would not be applicable⁵. One main disadvantage of deep learning-based methods is the necessity of acquiring sufficient training data with good gold-standard water-fat separation. This would have to be repeated for any new sequence and for any new anatomy, which is a deterrent for general clinical application.

In this abstract we describe a deep learning-based Dixon method with chemical-shift correction that was trained purely with simulated random data, and thus readily generalizes to new acquisitions simply by changing the simulation parameters. We demonstrate this method on three anatomies with varying scan parameters.

Methods

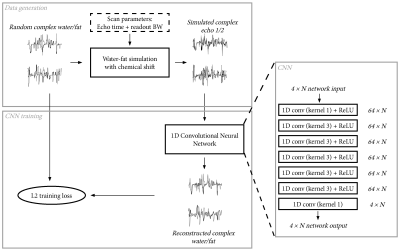
Convolution neural network:
We trained a 1D convolution neural network (CNN) that operates in the readout direction for separating water and fat with correction for chemical-shift from two complex-valued echoes. The CNN consisted of seven 1D convolution layers followed by a ReLU activation function. The network was trained with the Adam optimizer⁶ with an L2 loss function, and with a learning rate of 0.001 that was gradually decreased to 0 at the end of training. Each network was trained with a total of 3.3M training samples divided into 800 mini-batches, with a total training time of around 2.5 minutes on a Titan RTX GPU. The network training and data generation process is shown in Figure 1.

Training data generation:
The training data for the network was produced by simulating the acquisition for random 1D water ($$$w$$$) and fat ($$$f$$$) signals. Here, the acquisition was described by the echo times and readout bandwidth, which were included in a 6-peak fat model ($$$fat(t(k))$$$, where $$$t(k)$$$ is the echo time at k-space location $$$k$$$). The simulated signal ($$$s$$$) was calculated in k-space:
$$S_k=W_k+F_k\cdot fat(t(k)), \text{where} \: W=FFT(w), F=FFT(f), S=FFT(s)$$
The water and fat signals were generated from a piecewise constant magnitude and fat fraction. Optionally, a random phase was applied to both the water and fat signals to allow reconstruction of complex-valued water and fat. Finally, noise was added to the simulated signals to train the CNN to be robust to some noise.

Experimental data:
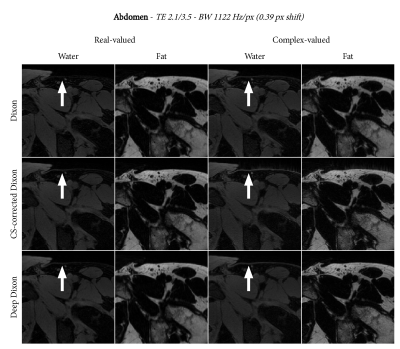
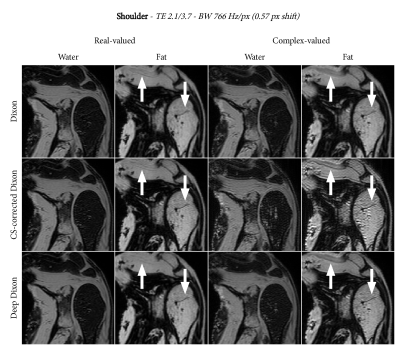
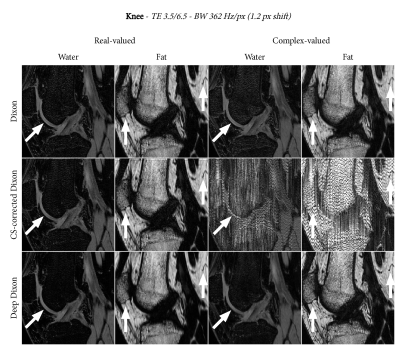
We applied the deep Dixon reconstruction to scans of the abdomen, shoulder, and knee. The relevant scan parameters were as follows:

Abdomen: $$$1.2\times1.2\times2.0$$$ mm resolution, TE₁/TE₂ 2.1/3.5, readout bandwidth 1122 Hz/px
Shoulder: $$$0.8\times0.8\times2.0$$$ mm resolution, TE₁/TE₂ 2.1/3.7, readout bandwidth 766 Hz/px
Knee: $$$0.5\times0.5\times1.3$$$ mm resolution, TE₁/TE₂ 3.5/6.5, readout bandwidth 362 Hz/px

Prior to applying the CNN, the background field was removed using conventional estimation of the background field phasor candidates^7, followed by region growing. For comparison, conventional k-space-based chemical-shift corrected Dixon was applied to the same data³. For both methods, both real-valued and complex-valued water and fat were reconstructed.

Results

Figures 2, 3, and 4 show the water-fat separation results for the abdomen, shoulder, and knee using both conventional and the deep Dixon approach. In general, we observe that chemical-shift correction improves the sharpness in the images. For real-valued water and fat, the deep Dixon results were mostly equivalent to the conventional method. However, for complex-valued water and fat, the conventional method showed streak artifacts caused by ill-conditioned linear systems in certain regions of k-space. This gets worse with lower readout bandwidth, which clearly shows in the high resolution knee images (Figure 4). The deep Dixon method was not affected by this, and often produced the clearest images out of all water-fat separations performed in this study.

Discussion & Conclusion

We demonstrated a deep learning-based Dixon water-fat separation method with chemical-shift correction that only requires randomly simulated training data. Our results show that the deep Dixon reconstruction is at worst equivalent, but often superior to conventional chemical-shift corrected Dixon, especially for complex-valued reconstructions that suffer from ill-conditioned problems in the conventional method.

A major difference of the deep Dixon method is that only knowledge of the forward operation (i.e. simulation) is required, whereas conventional approaches require designing solvers for the inverse problem. This makes other parameters, such as T₂^*, easier to include. Constraints and regularization can be introduced through data generation. For example, solving for real-valued water and fat simply means generating training samples with only real-valued water and fat. In comparison, the conventional chemical-shift corrected Dixon solver exploits the Hermitian symmetry of k-space of real-valued signals. Promoting smoothness in the produced result can be achieved by introducing smoothness in the generated water and fat signals, whereas for a conventional solver a mathematical and often differentiable definition of smoothness is required.

The deep Dixon approach demonstrates a fundamentally different way of solving the chemical-shift corrected water-fat separation problem. Its formulation is simple and extendable, and can likely be applied to more complicated inverse problems with more parameters.

Acknowledgements

This work is part of the research programme Applied and Engineering Sciences (TTW) with project number 15479 which is (partly) financed by the Netherlands Organization for Scientific Research (NWO).

References

1. Dixon WT. Simple proton spectroscopic imaging. Radiology. 1984;153(1):189–194.

2. Yu H, McKenzie CA, Shimakawa A, et al. Multiecho reconstruction for simultaneous water-fat decomposition and T2* estimation. J. Magn. Reson. Imaging. 2007;26(4):1153–1161.

3. Lu W, Yu H, Shimakawa A, et al. Water–fat separation with bipolar multiecho sequences. Magn. Reson. Med. 2008;60(1):198–209.

4. Goldfarb JW, Craft J, Cao JJ. Water–fat separation and parameter mapping in cardiac MRI via deep learning with a convolutional neural network. J. Magn. Reson. Imaging. 2019;50(2):655–665.

5. Andersson J, Ahlström H, Kullberg J. Separation of water and fat signal in whole-body gradient echo scans using convolutional neural networks. Magn. Reson. Med. 2019;82(3):1177–1186.

6. Kingma DP, Ba LJ. Adam: A Method for Stochastic Optimization. Int. Conf. Learn. Represent. ICLR. 2015.

7. Berglund J, Ahlström H, Johansson L, et al. Two-point dixon method with flexible echo times. Magn. Reson. Med. 2011;65(4):994–1004.

Figures

Figure 1. Overview of the convolutional neural network (CNN) training. Random water-fat signals are generated, from which the complex echo 1 and 2 signals are simulated. The simulated data serves as training input, while the generated water-fat signals serve as training output. The CNN operates on 1D signals in the readout dimension and has receptive field of 11 voxels.

Figure 2. Water-fat separation on the abdomen with conventional and the proposed deep Dixon methods. Both real-valued (left) and complex-valued (right) solutions were considered. Clear improvement is visible on the skin (arrows), where chemical-shift correction improves the thin water signal that was obscured by chemical-shift.

Figure 3. Water-fat separation on the shoulder with conventional and the proposed deep Dixon methods. Both real-valued (left) and complex-valued (right) solutions were considered. Arrows indicate regions where the sharpness of the image improves with chemical-shift correction.

Figure 4. Water-fat separation on the knee with conventional and the proposed deep Dixon methods. Both real-valued (left) and complex-valued (right) solutions were considered. The arrows on the fat images indicate a region where the sharpness of the image improves with chemical-shift correction. The arrows on the water images shows correction of a hyper-intense signal in the cartilage that was caused by chemical-shift. Note that the complex-valued conventional CS-corrected Dixon images are severely affected by ill-conditioned linear systems in certain regions of k-space.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3586