Introduction

In multi-compartmental T2 relaxometry, a multi-exponential MRI signal is inverted to quantify myelin water content (1)(2). This quantitative analysis allows diagnosing demyelinating diseases and evaluating the efficacy of their treatments (2). Currently, multi-exponential inversion is done by numerical optimization methods, like nonlinear least squares (NLS) (3). However, these methods are computationally expensive, sensitive to the selection of initial values and susceptible to local minima (4). There has been increasing interest in exploiting the ability of neural networks to approximate arbitrary to solve inverse problems. One such example is the use of simple artificial neural network — one hidden layer with 10 neurons — to estimate the parameters of a highly nonlinear MRI signal function (6). In this study, a different neural network architecture is proposed that is shown to perform multi-compartmental T2 relaxometry faster and more accurately than previous methods.

Methods

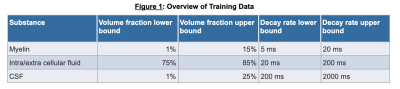
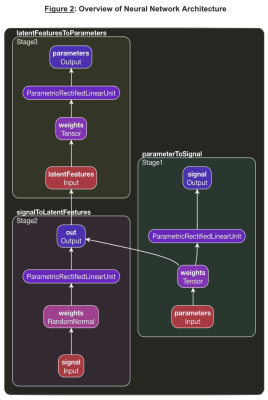
T2 Spectrum Acquisition. A multi-exponential T2 decay was simulated as $${\alpha}_1e^{\frac{TE}{T2_1}} + {\alpha}_2e^{\frac{TE}{T2_2}} + {\alpha}_1e^{\frac{TE}{T2_2}}$$ (2), where $$${\alpha}_1$$$, $$${\alpha}_2$$$, $$${\alpha}_3$$$ represents the volume fraction for myelin, CSF, and intra/extra-cellular fluid respectively and $$$T2_1$$$, $$$T2_2$$$, $$$T2_3$$$ are the corresponding T2 decay rates. Values for $$$\alpha$$$ and T2 were uniformly chosen between clinically relevant bounds as shown in Figure 1. The signals were simulated at various TEs (0.0, 7.5, 17.5, 67.5, 147.5, and 307.5 ms). 10,000 signals were simulated for training with mean 0 gaussian noise at standard deviation 1/100. In vivo data acquired in 5 healthy subjects and reconstructed using a previously proposed fitting NLS method (1) serving as the ground truth was available for training as well.
Network: A multi-staged deep neural network, called Deep Inversion Net, was constructed as shown in Figure 2. The first stage receives the parameters for the T2 multi-exponential decay and creates a 100 dimensional latent representation of the parameters to reconstruct the T2 signal. The second stage receives the T2 signal and maps it to the latent representation created by the first stage. The third stage receives the latent representation and then generates the parameters for the respective T2 decay. This communication between the first and second stage regularizes the networks. The incorporation of this latent representation generated by the first stage helps it extract important features about the multi-exponential decay. The network was trained on both the simulated data (10000 for training and 10000 for testing/validation) as well as one randomly selected healthy brain and tested on 4 brains.
Analysis: The performance of Deep Inversion Net was compared to NLS and an ANN with one hidden layer. Given that the T2 and $$$\alpha$$$ are in different units (ms and percentage), each algorithm’s accuracy was evaluated using mean absolute relative error: $$\frac{\Vert{f(x)−f(\hat{x})}\Vert_2^2}{\Vert{f(x)}\Vert_2^2}$$. These three networks were evaluated on both simulated data and real brain data.

Results

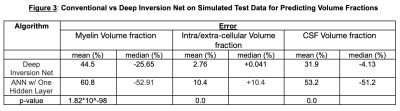
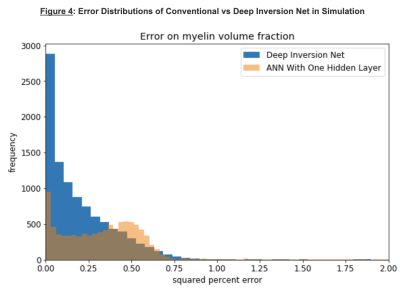
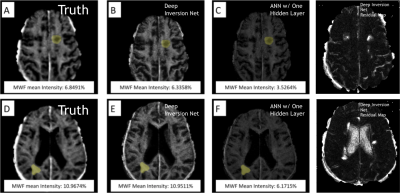
Accuracy
Simulations: Figures 3 and 4 show a comparison between Deep Inversion Net, NLS, and an ANN with one hidden layer. The proposed network achieved statistically significant improvements for accuracy on the simulated data. Additionally, the median error for Deep Inversion Net is closer to 0% than for the ANN. A median of 0% suggests that the model is not biased towards either underpredicting or overpredicting. Both the proposed and conventional neural networks seem to be biased towards underprediction. The beneficial impacts of mitigating these biases become very clear when looking at brain data. Although Deep Inversion Net’s improved accuracy could be attributed to its algorithmic complexity, the same network with the same amount of hidden layers and weights that did not contain smaller neural networks regularizing each other and passing on information about the exponential decay’s latent features had significantly lower accuracy for predicting certain parameters.
Real Brain: The ANN with one hidden layer gave inaccurate myelin maps on the testing set. Clinically, myelin water fraction in the brain ranges from 0-15%. However, the ANN with one hidden layer only generated predictions from 2.9%-4.0%. In simulation, the ANN had a significant under-estimation, which is again seen in real brain data. Deep Inversion Net, on the other hand, produced myelin maps that were similar to those generated using NLS.
Speed
Deep Inversion Net (and the ANN) produced myelin maps in under 2 seconds, while NLS took around 20-30 minutes.

Discussion and Conclusion

This study introduces a novel deep learning architecture that uses the outputs of multiple neural networks to regularize each other within a single neural network. Our data indicate the feasibility of this approach for multi-exponential T2 relaxometry inversion. In simulation, Deep Inversion Net vastly outperforms NLS in speed and ANN with one hidden layer in accuracy. In brain data and using NLS as ground truth, Deep Inversion Net produces more accurate myelin maps than ANN and produces these maps in significantly less time compared to NLS.

Acknowledgements

I would like to thank Prof. Nguyen, and Prof. Wang for advising me on this project. I would like to thank Prof. Wang, Prof. Spincemaille, and Prof. Nguyen for their support throughout the research process. I would like to thank the Weill Cornell Radiology Lab for all their support. I would also like to thank Jinwei Zhang and Junghun Cho for their support.