Introduction

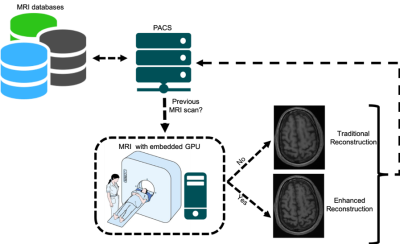
Deep-learning-based models for compressed sensing (CS) magnetic resonance (MR) image reconstruction is an active research field. Previous works have explored sparsity within a static MR sequence,¹ a dynamic MR sequence,² and across different MR sequences³ during the same examination. We propose to use images obtained from a previous scan of the same subject to enhance reconstruction of a follow-up exam. Previous scans are widely accessible with modern picture archiving and communication systems (PACS) and they we will show that they can provide additional information for the reconstruction process that can potentially support higher CS MR acceleration factors (Figure 1).

Materials and Methods

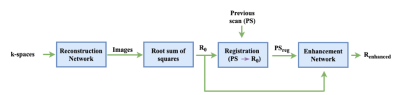
Our method (Figure 2) consists of a reconstruction network that receives as input multi-channel (MC) under-sampled k-space data and outputs MC images that are combined through root sum of squares⁴ to obtain an initial reconstruction (R₀). Then, a previous scan (PS) is linearly registered⁵ to R₀ (PS_reg). The final step is the enhancement network that receives as input a 2-channel image, consisting of R₀ and PS_reg, and produces the enhanced image (R_enhanced). For the reconstruction network, we used a WW-net (i.e., a cascade of two W-nets⁶) alternating between image and k-space domains with data consistency blocks in between. The enhancement network is a U-net.⁷ The dataset has 87 three-dimensional (3D), T1-weighted, gradient-recalled echo, sagittal acquisitions collected on a clinical 3-T MR scanner (Discovery MR750; General Electric (GE) Healthcare, Waukesha, WI). The scans correspond to presumed healthy subjects between 20 and 80 years (average: 45 years ± 16 years [mean ± standard deviation]). Datasets were acquired using a 12-channel coil. Acquisition parameters were either TR/TE/TI = 6.3 ms/2.6 ms/650 ms or TR/TE/TI = 7.4 ms/3.1 ms/400 ms, with 170 to 180 contiguous 1.0-mm slices and a field of view of 256 mm ×218 mm. The acquisition matrix size for each channel was N_x×N_y×N_z = 256×218×[170,180]. The scanner automatically applied the inverse FT, using the fast Fourier transform (FFT) algorithms, to the k_x-k_y-k_z-space data in the frequency-encoded direction, so a hybrid x-k_y-k_z dataset was saved. This reduces the problem from 3D to 2D, while still allowing to under-sampled of k-space in the phase encoding (k_y) and slice encoding (k_z) directions. The reference data were reconstructed by taking the channel-wise iFFT of the collected k-spaces for each slice of the 3D volume and combining the outputs by root sum of squares.⁴ The reconstruction network train/validation/test split was 43/18/13. The enhancement network train/validation/test was 18/7/13 corresponding to the 38 subjects that had pairs of scans (i.e., PS and following scan). The time between scans varied from one day to six months. Both the reconstruction network and the enhancement network were trained for 50 epochs using a mean squared error objective function. The models were trained for four different acceleration factors R=5×, 10×, 15×, and 20× using retrospective under-sampling. The models were assessed against the fully sampled reconstruction using structural similarity (SSIM), normalized root mean squared error (NRMSE) and peak signal to noise ratio (pSNR).

Results and Discussion

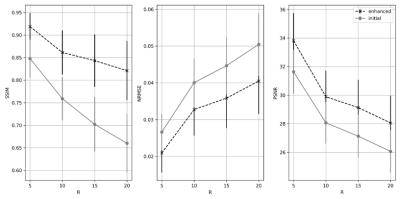
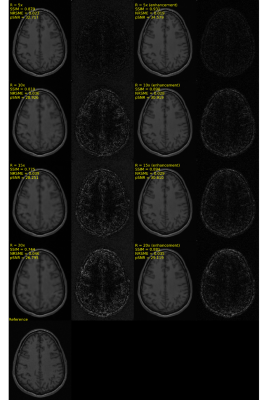
SSIM, NRMSE and pSNR metrics are depicted in Figure 3. Slices without any anatomical structure (i.e., only noise) were removed from the analysis. The enhanced reconstruction increased SSIM and PSNR on average by 16.7% and 7.6%, respectively, while it reduced NRMSE on average by 22.3% compared to the non-enhanced reconstruction. The difference between the enhanced and non-enhanced reconstruction metrics were found to be statistically significant (p<0.01, Wilcoxon test⁸), for all accelerations and metrics investigated. Visual inspections of the outliers indicated that these corresponded to slices showing little anatomical structures. A typical MR reconstruction representative of our results is depicted in Figure 4. After applying the enhancement network, reconstructed images become sharper. In our dataset, we are dealing with presumed normal subjects whose brains are not expected to change significantly in the follow-up scan time frame and the linear registration of the PS to the following scan worked in all cases. Although our results are encouraging, further testing needs to be done on different cohorts, including patient with evolving disease. The reconstruction network and enhancement network take < 10 s to reconstruct a volume using a Tesla V100 graphics processing unit. Nevertheless, the registration step took ~90 seconds. Therefore, the total combined reconstruction time was ~100 s, which is potentially prohibitive for real-time reconstruction, tough the registration step can potentially be more efficient.

Conclusions

We proposed a deep learning model that leverages information from previous scans to enhance the CS MR reconstruction of follow-up scans. In a cohort of presumed normal, adult subjects, we had an average improvement on all quantitative metrics of 15%. This methodology may allow to accelerate even further MR examinations. As future work, we intend to reproduce our methodology on a cohort of glioblastoma subjects that are being scanned longitudinally. This experiment is expected to be more challenging, because we expect temporal changes in the brain of these subjects.

Acknowledgements

The authors would like to thank NVidia for providing a Titan V GPU, Amazon Web Services for access to cloud-based GPU services R.S. was supported by an NSERC CREATE I3T Award and the T. Chen Fong Fellowship in Medical Imaging from the University of Calgary. W.L. acknowledges the University of Calgary Eyes High Fellowship. M.B. was supported by the Canadian Open Neuroscience Platform Fellowship. R.F. holds the Hopewell Professorship of Brain Imaging at the University of Calgary.