3502
Improving Dynamic Paralleling Imaging Reconstruction using Multi-Dimensional Integration (MDI)1UIH America, Inc., Houston, TX, United States, 2Paul C. Lauterbur Research Centre for Biomedical Imaging, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, 3Henan Chest Hospital, Zhengzhou, China, 4United Imaging Healthcare, Shanghai, China
Synopsis
We have developed and demonstrated a novel strategy for accurate estimation of coil sensitivity profiles for time-resolved data. Instead of direct temporal average to reduce noise in ACS, the proposed multi-dimensional integrated (MDI) strategy solves the least square problem for coil sensitivity profiles estimation in a new fashion. By extracting the overall calibration equations in all temporal dimensions, MDI is able to calculate coil sensitivity profiles more accurately than without this strategy. It can also be integrated with other parallel imaging methods such as SENSE and ESPIRiT.
Introduction
In dynamic parallel imaging, a time-interleaved acquisition scheme can be used, which eliminates the need for separately acquiring additional reference data. To improve the reconstruction condition and alleviate the noise amplification, this abstract presents a novel method by extracting calibration equations under the multi-dimensional integration (MDI) framework. With MDI, signal with extra dimensions (such as cardiac motion dimension, echo time dimension, flip angle dimension, dynamic contrast enhancement dimension) can be integrated to reduce noise level in both coil sensitivity maps and reconstructed images.Methods
In GRAPPA [1], the missing k-space data is estimated via a linear combination of the acquired under-sampled data in the neighborhood from all coils, which can be represented as$$b = A x,$$
where $$$A$$$ represents the matrix comprised of the acquired data, $$$b$$$ denotes the vector of the missing data, and $$$x$$$ represents the coefficients. In general, the coefficients depend on the coil sensitivities and are not known a priori. In GRAPPA, some auto-calibration data are acquired and used as the vector $$$b$$$ to estimate the coefficient vector $$$x$$$. The vector $$$b$$$ includes all ACS locations except the boundary regions in ACS to fit GRAPPA coefficients to all ACS data. In this case, the least-squares method is commonly used to calculate the coefficients: $$$x ̂=min_x ‖b-Ax‖^2$$$.
Consider a data set (2D or 3D) $$$y(t_c, n_e, t_d )$$$ has multiple time dimensions (cardiac motion, relaxation, perfusion) [2] and multiple channels. The linear relationship for each dimension can be represented as: $$b (t_c, n_e, t_d )= A(n_e, t_c, t_d) x,$$
where $$$t_c, n_e , t_d$$$ represent the cardiac motion, $$$T1/T2/T2^*$$$ relaxation, and perfusion dimension, respectively; $$$b(n_e, t_c, t_d)$$$ and $$$A(n_e, t_c, t_d)$$$ come from $$$y(n_e, t_c, t_d)$$$. With MDI, the coefficient vector $$$x$$$ for parallel imaging can be obtained:
$$x ̂=min_x \sum_{i=1}^{n_e} \sum_{j=1}^{t_c} \sum_{k=1}^{t_d} ‖b_{i,j,k} - A_{i,j,k}x‖^2 $$
where $$$i,j,k$$$ counts each of the time dimensions.
Mathematically , $$$x$$$ can also be written as: $$x ̂=\frac{\sum_{i=1}^{n_e}\sum_{j=1}^{t_c} \sum_{k=1}^{t_d}A^T_{i,j,k}b_{i,j,k}}{\sum_{i=1}^{n_e}\sum_{j=1}^{t_c} \sum_{k=1}^{t_d}A^T_{i,j,k}A_{i,j,k}} $$
Since there are more equations involved in the MDI framework, the coefficient vector $$$x$$$ can be calculated more accurately with reduced noise.
Results
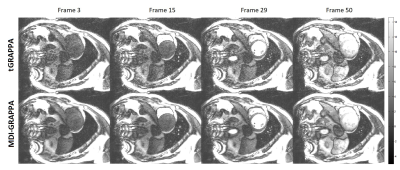
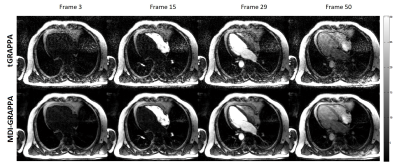
Prospectively accelerated free-breathing real-time cardiac cine imaging studies were performed on a 3T scanner (uMR 770, United Imaging Healthcare, Shanghai, China) with a 24-channel cardiac coil. A balanced steady-state free precession (BSSFP) sequence with time-interleaved undersampling scheme along the phase encoding dimension was used for data acquisition [5,6]. A patient (Male, 31 years old) was recruited and experimented with 2× accelerations. The common imaging parameters were TE/TR = 1.25/2.76ms, flip angle = 45°, FOV = 330 × 330mm2 , imaging matrix size = 192 × 144, slice thickness = 8mm, 50 cardiac phases, and phase resolution = 75%. The average of all frames along the temporal direction severed as the ACS data as in the conventional TGRAPPA reconstruction [5]. This especially benefited proposed MDI-GRAPPA for more accurate kernel estimation than GRAPPA.Figures 1~2 demonstrate the reconstruction results of the first-pass perfusion cardiovascular magnetic resonance. Conventional TGRAPPA reconstruction suffers from significant noise amplification. MDI-GRAPPA improve noise suppression and thus image quality.
Conclusion and Discussion
We have developed and demonstrated a novel strategy MDI, for accurate estimation of coil sensitivity profiles across multi dimensions. Instead of direct temporal average to reduce noise in ACS, MDI solves the least square problem for coil sensitivity profiles estimation by extracting the overall calibration equations. Preliminary demonstrated that, in Figs. 1&2, MDI-GRAPPA using temporal un-averaged data offers significantly better SNR and less noise. MDI is a framework that exploit the overall information across multiple dimensions. It can also be integrated with other parallel imaging methods such as SENSE [7], ESPIRiT [8].Acknowledgements
No acknowledgement found.References
1. Griswold, Mark A., Peter M. Jakob, Robin M. Heidemann, Mathias Nittka, Vladimir Jellus, Jianmin Wang, Berthold Kiefer, and Axel Haase. "Generalized autocalibrating partially parallel acquisitions (GRAPPA)." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 47, no. 6 (2002): 1202-1210.
2. Christodoulou, Anthony G., Jaime L. Shaw, Christopher Nguyen, Qi Yang, Yibin Xie, Nan Wang, and Debiao Li. "Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging." Nature biomedical engineering 2, no. 4 (2018): 215.
3. Lyu J, Liang D, Zhang C, Nakarmi U, and Ying L, A Blind Deconvolution Approach to Fast MR T2 Mapping, no. 1530, Proceedings of 25th Scientific Metting, International Society for Magnetic Resonance in Medicine, 2017.
4. Ye Y, and Lyu J, MR Relaxivity Mapping using multi-dimensional integrated (MDI) complex signal ratio, no. 4392, Proceedings of 27th Scientific Metting, International Society for Magnetic Resonance in Medicine, 2019.
5. Breuer FA, Kellman P, Griswold MA and Jakob P M, "Dynamic autocalibrated parallel imaging using temporal GRAPPA (TGRAPPA)." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 53, no. 4 (2005): 981-985.
6. Saybasili H, Kellman P, Griswold MA, DerbyshireA and Guttman MA, "HTGRAPPA: Real‐time B1‐weighted image domain TGRAPPA reconstruction." Magnetic Resonance in Medicine 61, no. 6 (2009): 1425-1433.
7. Pruessmann KP, Weiger M, Scheidegger MB, and Boesiger P, "SENSE: sensitivity encoding for fast MRI." Magnetic resonance in medicine 42, no. 5 (1999): 952-962.
8. Martin U, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, and Lustig M, "ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA." Magnetic resonance in medicine 71, no. 3 (2014): 990-1001.
Figures