3497
MoPED: Motion Parameter Estimation DenseNet for accelerating retrospective motion correction1Pattern Recognition Lab, Friedrich-Alexander-University Erlangen-Nuremberg, Erlangen, Germany, 2Siemens Healthcare GmbH, Erlangen, Germany, 3Erlangen Graduate School in Advanced Optical Technologies, Erlangen, Germany, 4Martinos Center for Biomedical Imaging, Charlestown, MA, United States
Synopsis
We exploit the data redundancy and the locality of motion in k-space for an estimation of the motion parameters using a Deep Learning approach. The exploratory Motion Parameter Estimation DenseNet (MoPED) extracts the in-plane motion parameters between echo trains of a TSE sequence. As input, the network receives the center patch of the k-space from multiple coils; the network’s output can serve multiple purposes. While an image rejection/reacquisition can be triggered by the motion guess, we show that motion aware reconstruction can be accelerated using MoPED.
Introduction
Despite a wide range of proposed motion correction methods1, patient movements during scanning remain as one of the main sources of artifacts in MR imaging2. Detecting if3,4 and when5 motion occurred as well as its severity6 is useful for rejecting or adapting the image reconstruction and shows the potential of Machine- and especially Deep Learning (DL) for treating motion. However, DL-based tomographic image reconstruction might be unstable7 and can also lead to undesired results.Combining a DL approach with model-based reconstruction8 takes an additional step to ensures data consistency and can avoid this pitfall. Building on motion detection5 and our previous work9, we present a new exploratory DL network that regresses the in-plane motion parameter for multiple echo trains (ET) from only the raw multi-coil k-space to allow an informed rejection of misaligned ETs or an improved initialized optimization of a motion-aware reconstruction.
Method
Dataset generation:Images and their sensitivity maps $$$\textbf{C}$$$ of 25 subjects and 4 phantoms (35 slices; transversal, sagittal and coronal) were acquired with a TSE sequence (TR=6100 ms, TE=103 ms, R=2, FOV=220 mm, resolution 448x448; on various Siemens MAGNETOM scanners, Siemens Healthcare, Erlangen, Germany at 1.5/3 T) and used for simulating in-plane motion (Translation Tx,y,l, Rotation Rz,l) for a given ET l. Therefore, a regular cartesian sampling trajectory $$$\textbf{S}_l$$$ with L=9 ETs (undersampling R = 2, 80% phase resolution, turbo factor = 20) was used to apply random integer motion trajectories (between -6- and +6 pixels translation/degree rotation) to a random and varying subset of ETs (between 0 and 6 ETs) of the Fourier transformed image kGT (Eq. 1). Prior to the simulation, noise and random flips were applied to the images for data augmentation.
$$\textbf{k}_{Mot}=∑_{l=0}^{L-1}S_lCT_{x,y,l}R_{z,l}k_{GT}\qquad\text{Eq. 1}$$
Processing pipeline:
The processing pipeline, depicted in Figure 1 a), utilizes the coil sensitivity maps to reduce the coil dimensionality of kMot by removing coils with less than the median mean absolute value and selecting the 4 most distant coils w.r.t. their sensitivity center of the remaining maps. The center is determined by the maximum value of the projection onto the axes. The remaining corresponding non-zero filled k-space is cropped to a 64x64x4 center patch and the complex values are split into additional channels. Each ET samples at least 7 lines in that crop and ensures that inter-ET motion is encoded within the input.
Neural Network and Training:
The Motion Parameter Estimation DenseNet (MoPED, see Figure 1b)) applies a DenseNet for feature extraction and finally maps them into the 3 motion parameters per ET. The multitask mapping of the feature vector consists of 2 fully connected layers separately for each ET for smoothing the training. Thus, each task is to learn the 3 parameters of one ET, which are then combined in a Lx3 (i.e. 27 total parameters) matrix for the loss function. The first fully connected layer before the multitask layers is added to avoid that mutual processing is learned redundantly for each ET.
The loss function is split into a) detection loss $$$\mathcal{L}_{detect}$$$ (Eq.2) being the sigmoid cross entropy between the thresholded network guess $$$\textbf{θ}_{Net} = \{\textbf{T}_x, \textbf{T}_y, \textbf{R}_z\}$$$ and ground truth motion $$$\overline{\textbf{θ}}_{GT}$$$ and b) $$$\mathcal{L}$$$mot, which calculates the L1 loss for all non-zero motion parameters. $$$\mathcal{L}$$$detect is weighted with λ=0.1.
$$\mathcal{L}_{detect}=D(\textbf{θ}_{GT} )(-\log(sig(D(\textbf{θ}_{Net}))))+(1-D(\textbf{θ}_{G}))(\log(-sig(D(\textbf{θ}_{Net}))))\qquad\text{Eq. 2}$$
$$D(x)=\begin{cases}0&|x|\geq0.4\\1&|x|<0.4\end{cases}$$
Following our previous work, the input is standardized followed by a trainable batch normalization before the first layer. The Xavier initialized network was trained employing the Adam optimizer.
Reconstruction:
The motion parameter estimation can trigger a threshold-based rejection of the acquisition or can be used as initial guess to obtain an improved image using for example a target voxel SENSE reconstruction combined with a motion model10. We compare the reconstruction results after 20 iterations with and without MoPED estimation.
Using the motion-aware reconstruction technique NAMER8 and assuming a perfect image guess, we compare the convergence speed for minimizing the residual motion estimation error against zero initialized motion.
Results
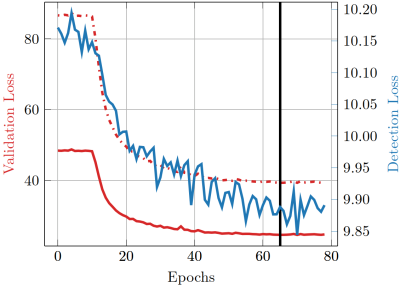
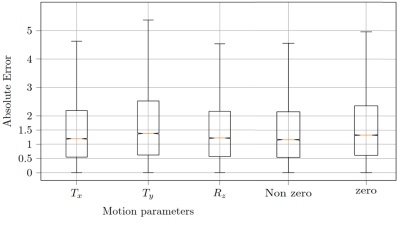
The loss curves during the training process are depicted in Fig. 2. In Fig 3, boxplots of the absolute error of the motion estimation over a validation data set are depicted, showing our desired focus on non-zero motion parameters.The images in Fig. 4 depict the reconstruction results after 20 iterations with and without MoPED initialization.
As the joint optimization of the image and motion parameter is highly non-linear, convergence can be slow. In Fig. 4, the MoPED initialization helps to overcome the stagnating convergence of the optimization.
Almost 80 samples are processed within one second, thus the MoPED allows a fast initial guess of the motion parameters (on a Nvidia Geforce GTX 1080 Ti).
The optimization of the residual parameters using the NAMER approach converged by an average of 18% faster.
Discussion and conclusion
The results show that our approach can retrospectively estimate motion solely from the reduced raw k-space as an initial guess without no external hardware or changes on the sequence. Nonetheless, an increased accuracy and focusing more on no/smaller motion is crucial and addressed, for example using Oksuz et al5, in future work.Regarding the convergence speed for a full reconstruction a thorough evaluation has yet to be done.
Acknowledgements
No acknowledgement found.References
1 Zaitsev M., Maclaren J., Herbst M. Motion artifacts in MRI: A complex problem with many partial solutions. J Magn Reson Imaging 2015; 42(4); 887-901
2 Andre J., Bresnahan B., Mossa-Basha M. et al. Toward Quantifying the Prevalence, Severity, and Cost Associated With Patient Motion During Clinical MR Examinations. J Am Coll Radiol 2016; 12(7); 689-95
3 Lorch B., Vaillant G., Baumgartner C. et al. Automated Detection of Motion Artefacts in MR Imaging Using Decision Forests. Journal of Medical Engineering 2017, 1-9
4 Arroyo-Camejo S., Odry B., Chen X. et al. Towards Contrast-Independent Automated Motion Detection Using 2D Adversarial DenseNets. Proc. ISMRM 2019 4868
5 Oksuz I., Clough J., Ruijsink B. et al. Detection and Correction of Cardiac MR Motion Artefacts during Reconstruction from K-space. Proc MICCAI 2019; 695-703
6 Hasiuk M., Pawar K., Zhong S. et al. Deep learning based motion estimation from highly under-sampled EPI volumetric navigators. Proc. ISMRM 2019 4448
7 Antun V., Renna F., Poon C. et al. On instabilities of deep learning in image reconstruction - Does AI come at a cost? CoRR 2019
8 Haskell M., Cauley S., Bilgic B. et al. Network Accelerated Motion Estimation and Reduction (NAMER): Convolutional neural network guided retrospective motion correction using a separable motion model. MRM 2019; 82(4)
9 Hossbach J., Splitthoff D., Haskell M. et al. Deep Neural Networks for Motion Estimation in k-space: Applications and Design. Proc. ISMRM 2019 4851
10 Haskell M., Cauley S., Wald L. TArgeted Motion Estimation and Reduction (TAMER): Data Consistency Based Motion Mitigation for MRI Using a Reduced Model Joint Optimization. TMI 2018; 37(5); 1253-65
Figures
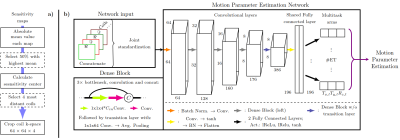
Fig 1: a) Processing pipeline for coil reduction. Based on the sensitivity maps, the 4 input coils for the MoPED are selected.
b) Sketch of the MoPED. The feature vector from of the Dense Blocks is reused for each ET and mapped into the 3 in-plane motion parameters using multitask learning. Convolutions (Conv.) consists of a 3x3x64 convolution, batch normalization and leaky ReLU (slope 0.1), if not stated otherwise in the figure.