Purpose

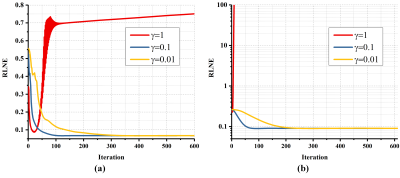
he emergence of sparse sampling and image reconstruction dramatically reduce the lengthy acquisition time of magnetic resonance imaging (MRI) ^1,2. Numerous efforts have been made to design sparse MRI reconstruction methods to achieve satisfactory results, and many works have shown that reconstruction models equipped with tight frame yield better results than those with orthogonal transform ^3,4 . Aiming at solving sparse MRI reconstruction problems under the tight frame, our group designed a projected iterative soft-threshold algorithm (pISTA) and its acceleration version – pFISTA ⁵. The pFISTA embraced low reconstruction error and fast convergence speed. Moreover, pFISTA has only one adjustable algorithm parameter $$$\gamma$$$ and its convergence criterion has been proved ⁵. The pFISTA, however, is limited to tackle single-coil image reconstruction problems. Recently, pFISTA has been applied to tackling parallel imaging reconstruction problems ⁶, such as sensitivity encoding (SENSE) method ⁷ and iterative self-consistent parallel imaging reconstruction (SPIRiT) ⁸. However, the convergence analysis of parallel imaging version pFISTA is not provided, and the convergence condition in single-coil pFISTA is not suitable for parallel imaging version pFISTA. A relatively large $$$\gamma$$$ will lead to the divergence while a far smaller one results in the slow convergence of the algorithm (Fig. 1) Therefore, it is necessary to give a clear mathematical proof of its convergence to assist setting a proper algorithm parameter.

Methods

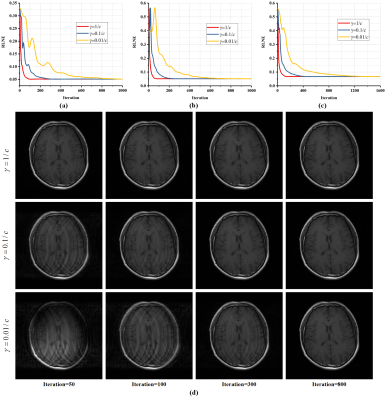
We proved the convergence of parallel imaging version pFISTA for both solving SENSE ⁷ and SPIRiT ⁸ optimization problems.
The reconstruction problem based on SENSE ⁷ can be formulated as: $$ {{\left ( \textbf{pFISTA-SENSE} \right )}} \quad \mathop {\min }\limits_{{{\mathbf{x}}_{c}}} \lambda {\left\| {{\bf{\Psi }}{{\bf{x}}_{c}}} \right\|_1} + \frac{1}{2}\sum\limits_{j=1}^{J}{\left\| {{\mathbf{y}} - {{{\mathbf{U}}}{{\mathbf{F}}}\mathbf{C}{{\mathbf{x}}_{c}}}} \right\|_2^2},$$ where $$${{\mathbf{x}}_{c}}$$$ denotes the composite MRI image, $$${{\mathbf{y}}_{j}} \left( j=1,2,\cdots ,J \right)$$$ the undersampled k-space vector of $$$j$$$^th coil, $$$\mathbf{U}$$$ the undersampling matrix, and $$$\mathbf{F}$$$ the discrete Fourier transform. $$${{\mathbf{C}}_{j}}$$$ is a diagonal matrix containing the sensitivity map of $$$j$$$^th coil, and $$$\mathbf{\Psi }$$$ is a tight frame. We provide the sufficient conditions for the convergence of pFISTA-SENSE in the form of a theorem.
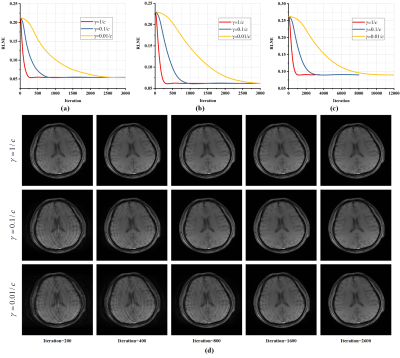
Theorem 1. Let $$$\left\{ {{x}^{\left( k \right)}} \right\}$$$ be generated by pFISTA-SENSE, and if the step size satisfies $$\gamma \le \frac{1}{c}, \quad c=\sum\limits_{j=1}^{J}{\left\| {{\mathbf{C}}_{j}} \right\|_{2}^{2}},$$ and $$$\mathbf{\Psi }$$$ is a tight frame, the sequence $$$\left\{ {{\alpha }^{\left( k \right)}} \right\}=\left\{ \mathbf{\Psi }{{x}^{\left( k \right)}} \right\}$$$ converges to a solution of $$\underset{\mathbf{\alpha }}{\mathop{\min }}\,\lambda {{\left\| \mathbf{\alpha } \right\|}_{1}}+\frac{1}{2}\left\| \mathbf{y}-\mathbf{UFC}{{\mathbf{\Psi }}^{*}}{{\mathbf{\alpha }}_{c}} \right\|_{2}^{2}+\frac{1}{2\gamma }\left\| \left( \mathbf{I}-\mathbf{\Psi }{{\mathbf{\Psi }}^{*}} \right)\mathbf{\alpha } \right\|_{2}^{2}.$$ The SPIRiT ⁸ reconstruction with $$$\ell_1$$$ constraint can be formulated as: $$ {{\left ( \textbf{pFISTA-SPIRiT} \right )}} \quad \mathop {\min }\limits_{\mathbf{x}} \lambda {\left\| {{\mathbf{\Psi x}}} \right\|_1} + \frac{1}{2} \left\| {{\mathbf{y}} - {{\mathbf U}{\mathbf{F}}\mathbf{x}}} \right\|_2^2 + \frac{\lambda _1}{2} \left\| {\left( {{\mathbf{G}} - {\mathbf{I}}} \right){{\mathbf F}\mathbf{x}}} \right\|_2^2, $$ where $$$\mathbf{x}=\left[ {{\mathbf{x}}_{1}};{{\mathbf{x}}_{2}};\cdots ;{{\mathbf{x}}_{J}} \right]$$$ denotes the multi-coil MRI image data rearranged into a column vector, and$$$\mathbf{y}=\left[ {{\mathbf{y}}_{1}};{{\mathbf{y}}_{2}};\cdots ;{{\mathbf{y}}_{J}} \right]$$$ the undersampled multi-coil k-space data. The matrix $$$\mathbf{G}$$$ consists of a series of matrices $$${{\mathbf{G}}_{j,i}} \left( i,j=1,\cdots ,J \right)$$$, which represent the linear combination weights in SPIRiT.
Also, we provide the sufficient conditions for the convergence of pFISTA-SPIRiT in the form of a theorem.
Theorem 2. Let $$$\left\{ {{x}^{\left( k \right)}} \right\}$$$ be generated by pFISTA-SPRIT, and if the step size satisfies $$ {\gamma} \le \frac{1}{c},\quad c=1+{{\lambda }_{1}}{{\left( \sum\limits_{m=1}^{J}{\sum\limits_{n=1}^{J}{{{\left\| {{\mathbf{G}}_{m,n}} \right\|}_{2}}}}+1 \right)}^{2}},$$ and $$$\mathbf{\Psi }$$$ is a tight frame, the sequence $$$\left\{ {{\alpha }^{\left( k \right)}} \right\}=\left\{ \mathbf{\Psi }{{x}^{\left( k \right)}} \right\}$$$ converges to a solution of $$\underset{\mathbf{\alpha }}{\mathop{\min }}\,\lambda {{\left\| \mathbf{\alpha } \right\|}_{1}}+\frac{1}{2}\left\| \mathbf{y}-\left[ \begin{matrix} {\mathbf{\tilde{U}}} \\ -\sqrt{{{\lambda }_{1}}}\left( \mathbf{G}-\mathbf{I} \right) \\ \end{matrix} \right]\mathbf{F}{{\mathbf{\Psi }}^{*}}\mathbf{\alpha } \right\|_{2}^{2}+\frac{1}{2\gamma }\left\| \left( \mathbf{I}-\mathbf{\Psi }{{\mathbf{\Psi }}^{*}} \right)\mathbf{\alpha } \right\|_{2}^{2}.$$

Results

As shown in Fig. 2 and 3, for three tested brain images, when using the $$$\gamma $$$ ranged from $$$0.01/c$$$ to $$$1/c$$$, pFISTA-SENSE and pFISTA-SPIRiT empirically converge to a level of promising low relative $$$\ell_2$$$ norm (RLNE). The larger the $$$\gamma $$$, the faster the algorithms converge, and the fastest convergence speeds are achieved when $$$\gamma =1/c$$$. Thus, we recommend $$$\gamma =1/c$$$ for both pFISTA-SENSE and pFISTA-SPIRiT experiments.

Conclusion

In this work, we proved the sufficient conditions for the convergence of parallel imaging version pFISTA, including pFISTA-SENSE and pFISTA-SPIRiT, for solving spare reconstruction models. Experimental results demonstrate the validity and effectiveness of the convergence criterion. This work is expected to help users quickly choose a proper parameter to obtain faithful results and fast convergence speed and to promote the application of sparse reconstruction.