Introduction

While being strengthful in clinical diagnosis, MRI suffers from several problems, huge volume, large mass and high cost, thus limiting its application in a wider range of scenarios. These problems could be solved to a great extent if the strength of static magnetic field could be reduced, which means a more compact MRI system. Low-field or accesible MRI have draw researchers' attention in recent years, and some work about low field MRI are reported.^1,2 In order to attain images of high quality, the scanning time in low-field MRI systems is expected to be longer compared to those high-field ones due to the intrinsic relative low SNR. Therefore, shortening the acquisition time under the low-field environment is crucial for the clinical promotion of low-field MRI, especially in the case of those disease deteriorating fast, stroke, for example.
Compressed sensing (CS) has proved highly effective in rapid MRI ^3-5, and the FDA approval of compressed sensing incorporated in some high-field products for clinical scans shows its superiority.⁶ In this work, we combine the low-rank model with compressed sensing in low-field MRI (0.05T) and simulations are conducted using in vivo data of stroke. The results illustrate the ability of this method in identification of stroke and preserving shape characteristics of the lesion region.

Methods

1.Low-rank matrix for images
Each image could be devided into small patches, many of which are similar to other ones. Representing patches as column vectors, a patch-based matrix could be constructed for each patch by gathering other patches similar to it. These matrices are expected to have the property of low-rank thanks to the high coherence among columns among each matrix, thus providing sparse representation for compressed sensing reconstruction.
2.Low-rank based Reconstruction model
Denote $$$T_{i}$$$ as an operator that extracts a patch $$$m_{i}$$$ from image $$$M$$$ and form the low-rank matrix $$$G_{i}$$$ by searching similar patches in a window of certain size. That is $$$G_{i}=T_{i}(M)$$$. To achieve better reconstruction result, we use a non-convex surrogate of the rank instead of the nuclear norm. As reported in the previous reference⁷, for a general matrix $$$G_{i}$$$, the rank minimization problem could be replaced by minimizing
$$$\log\det(g_{i})$$$ where $$$g_{i}$$$ is a diagonal matrix and its diagonal elements are the singular values of $$$G_{i}$$$. So the low-rank minimization could be realized by solving $$argmin {_{G_{i}}} \left(\log\det(g_{i})\right)+\mu\parallel T_{i}(M)-G_{i} \parallel_F^2$$.
Incorporating the data fedility constriant, the whole reconstruction model could be written as
$$argmin {_{G_{i},{M}}} \parallel Y-F_{u}M \parallel _2^2+\lambda\left(\sum\log\det(g_{i})+\mu\sum\parallel T_{i}(M)-G_{i} \parallel_F^2\right)$$, where $$$F_{u}$$$ denotes the undersampled Fourier transform operator and $$$Y$$$ denotes the measurements.
3.Optimization algorithm
Since the whole reconstruction model is non-convex and it 's hard to solve it directly, we propose to split it into two sub-minimization problems with respect to M and Gi.Then M and Gi could be updated alternatively in iteration.
The sub-minimization problem for $$$G_{i}$$$ is $$argmin {_{G_{i}}} \log\det(g_{i})+\mu\parallel T_{i}(M)-G_{i} \parallel_F^2$$

The optimization problem above could be surrogated by weighted nuclear norm. Given a warm start, it could be solved by the means of iterative single value thresholding.
The sub-minimization problem for M is $$argmin {_{G_{i},{M}}} \parallel Y-F_{u}M \parallel _2^2+\lambda\left(\mu\sum\parallel T_{i}(M)-G_{i} \parallel_F^2\right)$$
The minimization for M is a quadraic optimization problem, and we adopt gradient descent method to solve the sub-minimization problem for M.

Results

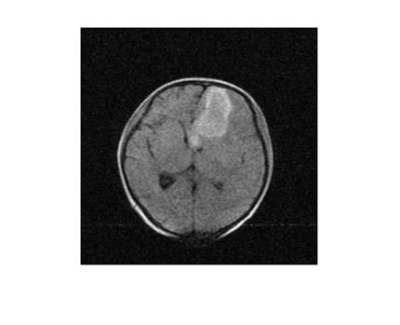
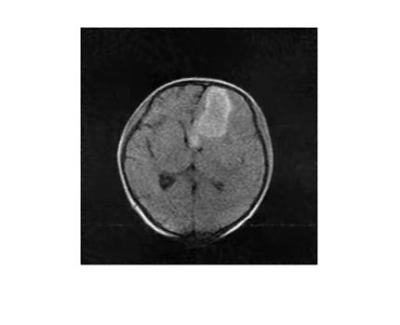
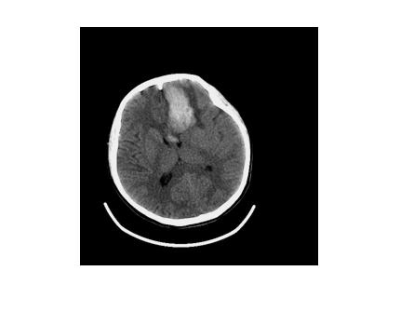
The fully sampled MR image with size 256*256 is shown in Fig.1. The image was acquired from a patient with cerebral hemorrhage at a 0.05T MRI scanner developed by our group in total time of 7minutes and 36secnods. The scanning was approved by the institutional research ethics committee of Southwest Hospital, Chongqing, China. Fig.2 shows the sampling pattern with sampling rate 0.2, and the undersampling is performed along the phase code direction with variable density. Fig.3 shows the reconstructed image using the proposed method. For comparison, the image from the same patient at a protable CT CereTom is also shown in Fig.4
The lesion region could be recognized in all three images. The shape features are well retained in the reconstructed image generated by the low-rank based CS method, though only 20% data is used.

Discussion

The proposed low-rank based compressed sensing method achieves satisfactory results, despite the relative low SNR in low-field MRI. The reconstructed image preserves almost all image details, and most importantly, it keeps the same hemorrhagic area as shown in CT image and fully sampled MR image.

Conclusion

Utilizing the similarity among patches of a image, the low-rank based compressed sensing works excellently when it comes to low-field MRI. The result demonstrates that reconstructed images could provide enough diagnostic basis even if in a highly undersampled condition (20% in this work).
Becoming Lighter, smaller and cheaper is the development trend of MRI in the sense of clinically providing timely diagnosis and treatment for those who are suffering from severe illness. Low-field and accessible MRI are likely to be used in a much more wide range of clinical scenarios in the future, and the technology of compressed sensing makes up for the shortcomings of relative long scanning time in a low-field environment, thus paving the way for the further promotion of low-field and accessible MRI in clinical.

Acknowledgements

The author would like to thanks Professor Wei He for his favorable guidance.