3479

Isotropic MRI Reconstruction with 3D Convolutional Neural Network
Xiaole Zhao1, Tian He1, Ying Liao1, Yun Qin1, Tao Zhang1,2,3, and Mark Zou1,2,3
1School of Life Science and Technology, University of Electronic Science and Technology of China, Chengdu, China, 2High Field Magnetic Resonance Brain Imaging Laboratory of Sichuan, Chengdu, China, 3Key Laboratory for NeuroInformation of Ministry of Education, Chengdu, China

Synopsis

Typical magnetic resonance imaging (MRI) usually shows distinct anisotropic spatial resolution in imaging plane and slice-select direction. Image super-resolution (SR) techniques are widely used as an alternative method to isotropic MRI reconstruction. In this work, we propose to reconstruct isotropic magnetic resonance (MR) volumes via 3D convolutional neural network in an end-to-end manner. 3D SRCNN is utilized to preliminarily validate the idea and it produces quantitative and qualitative results significantly superior to traditional methods, such as Cube-Avg and NLM methods.

Introduction

Magnetic resonance imaging (MRI) usually demonstrates severe anisotropic spatial resolution that hampers postprocessing, such as image segmentation and visualization etc. due to the limitations of hardware, physical and physiological factors. Recently, Image super-resolution (SR) techniques are widely used as an alternative to isotropic reconstruction. However, traditional SR methods suffer from poor performance, long running time and requirement for manual feature extraction. Inspired by the powerful representational capacity and the convenience of automatic feature extraction of convolutional neural networks (CNNs), we present an end-to-end isotropic MRI reconstruction method based on 3D CNNs that enable effective capture of 3D spatial features in MR volumes and accurate prediction of potential structure. Moreover, the model takes multiple orthogonal scans as input and therefore can use more complementary information from different dimensions for precise SR inference.

Methods

The network structure is inherited from the SRCNN1, which is expended to 3D space and used for the inference of isotropic reconstruction. Unlike Jia et al.3 that adopted dictionary learning and sparse representation for nonlinear inference, we utilize 3D SRCNN to nonlinearly speculate the potential isotropic counterpart. To make full use of complementary information from different directions (axial, coronal and sagittal), three orthogonal anisotropic volumes (scans) are upsampled by spline interpolation and fused together by element-wise average and then fed into the network for nonlinear mapping, as shown in Fig.1. We randomly select 155 volumes from HCP dataset4, and divide them into training set, testing set and validation set with 100, 50 and 5 volumes respectively. Both T1 and T2 data in HCP dataset are included in our experiments.

We extract 24×24×24 small cubes from low resolution (LR) volumes with their corresponding high resolution (HR) cubes from HR volumes for model training. Data augmentation is completed by flipping up and down, left and right, and back and forth. Batch size is set to 8 and the numbers of feature maps are set followed the 2D SRCNN1. We adopt L1 loss for model optimization, which is minimized by the Adam optimizer5 with β1 = 0.9, β2 = 0.999 and ε = 10-8. Learning rate is initialized as 2×10−4 and halved at every 1×105 iterations, with 4×105 iterations in total.

Results

We compare the proposed method with traditional cube average method (Cube-Avg)3 and nonlocal upsampling (NLM)2, and the commonly-used peak signal noise ratio (PSNR) and SSIM6 are used for quantitative evaluation. The quantitative comparison between these methods in terms of 6 scaling factors and 2 data types (T1 and T2) is shown in Table 1. It can be observed that the proposed methods can surpass traditional methods by a large margin, which is mainly due to the powerful nonlinear representational capacity of deep CNNs and the full use of complementary information of orthogonal scans. Fig. 2 shows the reconstruction results of the proposed method on a simulated T2 volume from the BrainWeb dataset in case of SR×5, whose ground truth has spatial resolution of 1mm×1mm×1mm. The corresponding anisotropic scans are also displayed for comparison purposes. We can observe that some structural details in the image are blurred and obscured in anisotropic scans. While in the results of our methods, these structures are recovered satisfactorily with high and isotropic resolution. Fig. 3 displays the visual comparison between these methods on a T1 volume from the HCP dataset. It can be seen that 3D SRCNN can achieve high quality isotropic MR reconstruction, even with large scaling factor (SR×7).

Discussion

In our experiments, the anisotropic LR volumes are generated from the original HR isotropic volumes by averaging adjacent slices, e.g., for SR×5, 5 adjacent slices are averaged to form a single slice in the anisotropic volume. This process is adopted to simulate the Partial Volume Effect (PVE), which may appear in different ways in practical anisotropic acquisitions and simulations of generated MR volumes. Moreover, the resolution of training data, noise level and other factors will also affect the actual deployment of the model. But these effects can be alleviated by simply including these factors in training data at the expense of a small amount of performance.

Conclusion

In this work, we preliminarily investigated the performance of deep CNNs in MR isotropic reconstruction by expanding SRCNN1 to 3D space and combining it with multiple orthogonal scans. The results exhibit that compared with traditional methods, the CNN-based methods can make effective use of the complementary information among the orthogonal scans to reconstruct MR volumes with high and isotropic resolution.

Acknowledgements

The work is supported in part by the National Key Researchand Development Program of China (No. 2016YFC0100800 and 2016YFC0100802).

References

  1. Dong C., Loy C. C., He K., et al. Image super-resolution using deep convolutional networks [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016; 38(2):295-307.
  2. Manjón J. V., Coupé P., Buades A., and et al. Non-local MRI upsampling [J]. Medical Image Analysis, 2010; 14(6): 784-792.
  3. Jia Y. Y., Gholipour A., He Z., Warfield S. K. A new sparse representation framework for reconstruction of an isotropic high spatial resolution MR volume from orthogonal anisotropic resolution scans [J]. IEEE Transactions on Medical Imaging, 2017; 36(5): 1182-1193.
  4. Glasser M. F., Sotiropoulos S. N., Wilson J. A., et al. The minimal preprocessing pipelines for the Human Connectome Project [J]. NeuroImage, 2013; 80: 105-124.
  5. Kingma D. P., Ba J., Adam: A method for stochastic optimization [C]. International Conference on Learning Representations (ICLR), 2015.
  6. Wang Z., Bovik A. C., Sheikh H. R., Simoncelli E. P. Image quality assessment: from error visibility to structural similarity [J]. IEEE Transactions on Image Processing, 2004; 13(4): 600-612.

Figures

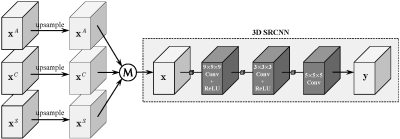
The flow diagram of our isotropic MR reconstruction using 3D convolutional neural network. The input of the 3D network is obtained by upsampling and averaging axial, coronal and sagittal scans. "M" denotes the operation of element-wise average.

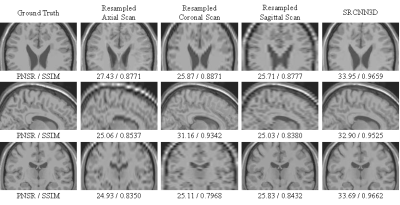
Reconstruction results of the proposed method compared with anisotropic scans. The model is tested on a simulated T2 volume from the BrainWeb dataset (SR×5, reconstruct from slice thickness = 5.0mm to 1.0mm). Top to button: Axial view, Sagittal view and Coronal view.

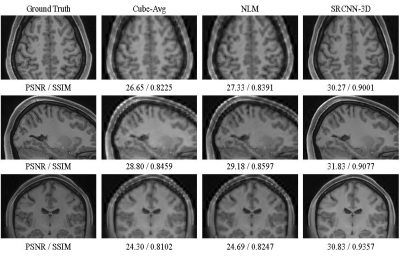
Visual comparison between the compared methods on a T1 volume from the HCP testing dataset. The resolution ratio between in-plane and slice-select directions is SR×7 (0.7mm×0.7mm×4.9mm).

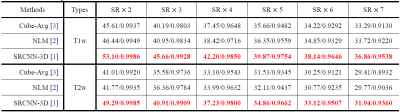
Quantitative comparison of 3 methods (Cube-Avg, NLM and SRCNN-3D) on 50 test volumes of the HCP dataset, in terms of 6 different scaling factors.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
3479