3477

Accelerated MR-STAT Algorithm: Achieving 10-minute High-Resolution Reconstructions on a Desktop PC
Hongyan Liu1,2, Oscar van der Heide1,2, Cornelis A.T. van den Berg1,2, and Alessandro Sbrizzi1,2
1Computational Imaging Group for MR Diagnostics and Therapy, Center for Image Sciences, University Medical Center Utrecht, Utrecht, Netherlands, 2Department of Radiology, Division of Imaging and Oncology, University Medical Center Utrecht, Utrecht, Netherlands

Synopsis

MR-STAT is a framework for simultaneous mapping of quantitative MR parameters from a single short scan. Since MR-STAT involves the solution of a large scale nonlinear optimization problem, the reconstruction time has always been one main concern. In the current work, we develop an accelerated MR-STAT algorithm, which achieves two order of magnitude acceleration in reconstruction times. High-resolution 2D dataset can be reconstructed within 10 minutes on a desktop PC thereby drastically facilitating the application of MR-STAT in the clinical work-flow.

Introduction

MR-STAT is a framework for obtaining multi-parametric quantitative maps from single short scan[1,2]. The parameter maps are reconstructed by iteratively solving the large scale, non-linear problem
$$\hat{\alpha }=\arg\min_{\alpha }\frac{1}{2}\left\Vert d-s( \alpha )\right\Vert^{2}_{2},\ \ \ (1)$$
where $$$d$$$ is the data in time domain, $$$\alpha$$$ denotes all parameter maps, and $$$s$$$ is the volumetric signal model. Although recent improvements have been obtained[2,3], MR-STAT reconstructions still lead to long computation times because of the large scale of the problem, requiring a high performance computing cluster for application in a clinical work-flow.
In this work, we drastically accelerate MR-STAT reconstructions by following two strategies, namely: 1) computing the signal and derivatives by a fast surrogate model and 2) adopting an Alternative Direction Methods of Multipliers[4]. The new algorithm achieves a two order of magnitude acceleration in reconstructions with respect to the state-of-the-art MR-STAT. A high-resolution 2D dataset is reconstructed within 10 minutes on a desktop PC thereby greatly facilitating the application of MR-STAT in the clinical work-flow.

Theory

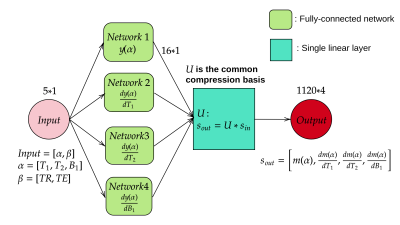
  • Surrogate MR signal Model
Since MR-STAT is solved by a derivative-based iterative optimization scheme, both the magnetization and its derivatives with respect to all reconstructed parameters need to be computed at each iteration using an MR signal model (EPG[5] or Bloch equation). To accelerate the signal computation, a neural network (NN) is designed and trained to learn the signal and derivatives for either balanced or gradient spoiled sequence. The NN architecture is shown in Figure 1. The NN consists of separate blocks for computing compressed magnetization and derivatives, and one final shared linear layer as a learnable compression operator which reduces the dimensionality of the problem to a low rank (in this work, rank = 16).

  • The ADMM approach
After applying the surrogate NN model and assuming Cartesian sampling, the original volumetric signal $$$s$$$ (Eq 1) can be factorized into different matrix operators, leading to the following form,
$$\hat{\alpha}=\arg\min_{\alpha}\frac{1}{2}\left\Vert D-\sum^{Ny}_{i=1}C^{p}_{i}UY(\alpha _{i})C^{r}(\alpha _{i})\right\Vert^{2}_{F}.\ \ \ (2)$$
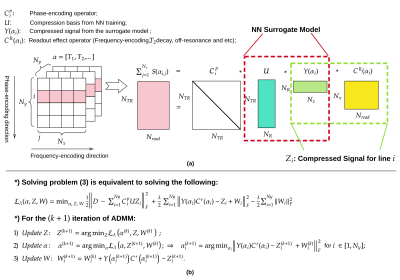
A graphic illustration of the new problem (2) and the explanation of the operators is shown in Figure 2(a).
We reformulate problem (2) as the following constrained problem
$$\hat{\alpha}=\arg\min_{Z,\alpha}\frac{1}{2}\left\Vert D-\sum^{Ny}_{i=1}C^{p}_{i}UZ_{i}\right\Vert^{2}_{F} \text{subject to }Y(\alpha _{i})C^{r}(\alpha _{i})-Z_{i}=0\text{ for }i\in [1,N_{y}],\ \ \ (3) $$
by adding slack variable $$$Z_i$$$. The corresponding alternating update scheme[4] is shown in Figure 2(b). In this scheme, step (1) solves a linear problem and step (2) solves $$$N_x$$$ small parallelizable nonlinear problems using the compressed signal, therefore substantially reducing the computational complexity w.r.t. the original MR-STAT.

Methods

Both balanced and gradient spoiled MR-STAT sequence are used in the current work with Cartesian acquisition and slowly varying flip angle trains[2].

  • Surrogate model training and validation
Neural networks are trained for balanced and spoiled signal models where the inputs are (T1, T2, B1, B0, TR, TE) and (T1, T2, B1, TR, TE), respectively. Imperfect slice profile is also modeled[5]. Training is performed with Tensorflow[6] using ADAM optimizer, 6000 epochs. The NN surrogate results are validated by both simulation results and measured data from a Philips Ingenia 1.5T scanner.

  • Accelerated MR-STAT reconstruction
The accelerated MR-STAT reconstruction algorithm incorporating the surrogate model and the ADMM splitting scheme is implemented in Matlab on a 8-Core desktop PC (3.7GHz CPU). To validate the reconstruction results, gel phantom tubes were scanned with a spoiled MR-STAT sequence on a Philips Ingenia 3T scanner, and an interleaved inversion-recovery and multi spin-echo sequence (2DMix, 7 minutes acquisition) provided by the MR vendor[7] was also scanned as a benchmark comparison.
For in-vivo validation, the standard and accelerated MR-STAT reconstructions are run on both gradient spoiled (scan time 9.8s, TR=8.7ms, TE= 4.6ms) and balanced (scan time 10.3s, TR=9.16ms, TE=4.58ms) acquisitions.

Results

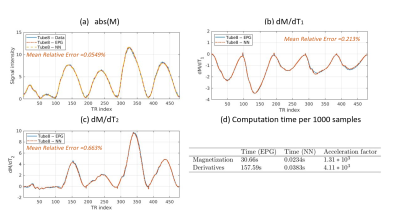
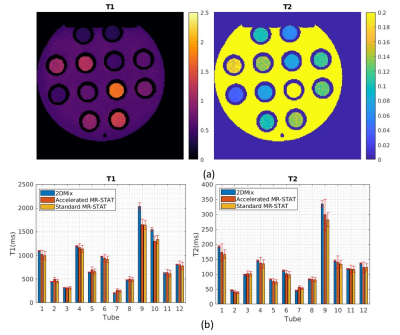
Figure 3 summarizes the validation results of the surrogate MR signal model, showing that the NN surrogate model achieves an acceleration factor of thousand with negligible errors.
Figure 4 shows high agreements in $$$T_1$$$ and $$$T_2$$$ maps obtained from standard MR-STAT reconstruction, accelerated MR-STAT reconstruction and a 2DMix acquisition for the gel phantom data.
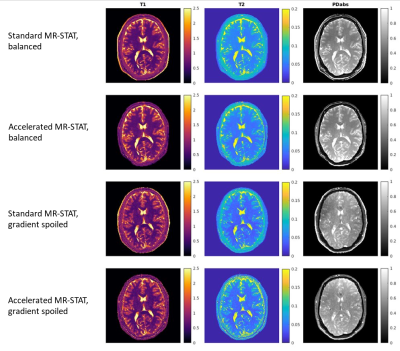
Figure 5 shows in-vivo results of one representative slice from a healthy human brain; both standard and accelerated MR-STAT algorithms obtain similar quantitative maps from both balanced and gradient spoiled acquisitions.
With the accelerated MR-STAT algorithm, one 2D slice reconstruction requires approximately 157 seconds with single-coil data, and 671 seconds with four compressed virtual coil data. Compared with the results reported previously (50 minutes single-coil reconstruction on a 64 CPU's cluster[3]), our accelerated algorithm obtains a two order of magnitude acceleration in reconstruction time.

Conclusion and Discussion

We presented a new MR-STAT reconstruction algorithm where both a Neural Network surrogate model and a variable splitting scheme are employed. Simulated, phantom and in-vivo experiments show that the new MR-STAT algorithm is two orders of magnitude faster than the conventional algorithm and can thus run in 10 minutes on a Desktop PC. Training of the NN takes about two hours in total, but the network is flexible and can be reused for sequences with different parameters (TE, TR).
This new implementation paves the way to the application of MR-STAT in the clinic, since the computation time is no longer a burden for the clinical work-flow.

Acknowledgements

The first author receives CSC(Chinese Scholarship Counsel) scholarship.

References

[1] Sbrizzi, Alessandro, et al. "Fast quantitative MRI as a nonlinear tomography problem." Magnetic resonance imaging 46 (2018): 56-63.

[2] van der Heide, Oscar, et al. "High resolution in-vivo MR-STAT using a matrix-free and parallelized reconstruction algorithm." arXiv preprint arXiv:1904.13244 (2019).

[3] van der Heide, Oscar, et al. "Sparse MR-STAT: Order of magnitude acceleration in reconstruction times." in ISMRM, Montreal, Canada, p. 4538 (2019).

[4] Boyd, Stephen, et al. "Distributed optimization and statistical learning via the alternating direction method of multipliers." Foundations and Trends in Machine learning 3.1 (2011): 1-122.

[5] Weigel, Matthias. "Extended phase graphs: dephasing, RF pulses, and echoes‐pure and simple." Journal of Magnetic Resonance Imaging 41.2 (2015): 266-295.

[6] Abadi, Martín, et al. "Tensorflow: Large-scale machine learning on heterogeneous distributed systems." arXiv preprint arXiv:1603.04467 (2016).

[7] In den Kleef, J. J. E., and J. J. M. Cuppen. "RLSQ: T1, T2, and ρ calculations, combining ratios and least squares." Magnetic resonance in medicine 5.6 (1987): 513-524.

Figures

Figure 1: NN architecture for the surrogate MR signal model. The input of the NN is a combination of reconstructed parameters (T1,T2,B1,B0) and sequence parameters (TR, TE). The output is the time-domain signal and its derivatives w.r.t. to all tissue parameters. The NN consists of separate blocks (sub-Networks 1-4) for computing the compressed magnetization and derivatives, each of which has four fully connected layers with ReLU activation function, and one final learnable linear layer which acts as a linear decoding step by means of the learnable U matrix.

Figure 2: Model factorization and the corresponding ADMM algorithm. (a): Graphic illustration of the new problem Eq. (2). Four operators are introduced to generate the full model: $$$C_i^p$$$, $$$U$$$, $$$Y(\alpha_i)$$$ and $$$C^r(\alpha_i)$$$ (definition given in the figure). (b): The ADMM algorithm with data $$$d$$$ formatted as a matrix $$$D$$$. In step (1), the compressed signals $$$Z_i$$$ are computed by solving a linear problem. In step (2), quantitative maps are obtained by solving separate nonlinear problems using a trust-region method.

Figure 3: Validation of the surrogate NN model. 3 gel tubes with different T1 and T2 values were scanned using a spoiled sequence, and time-dependent signal and derivatives from one tube (T1=612ms, T2=125ms) are shown. The other 2 tubes show similar results. In (a), the magnetization signal computed from the NN model is compared with EPG simulations and measured data. In (b) and (c), signal derivatives are compared with EPG results. Mean relative errors over a test set of 1000 random samples are also reported. Panel (d) shows the computational acceleration of NN w.r.t. the EPG model.

Figure 4: Comparison of experimental phantom results between accelerated MR-STAT and standard MR-STAT reconstruction. (a) $$$T_1$$$ and $$$T_2$$$ maps from accelerated MR-STAT reconstruction. (b) Bar plots of mean and standard $$$T_1$$$ and $$$T_2$$$ values for the twelve tube phantoms from both standard and accelerated MR-STAT reconstructions; 2DMix results are included for reference.

Figure 5: Comparison between standard and accelerated MR-STAT reconstructions. Quantitative maps including $$$T_1$$$, $$$T_2$$$ and PD from both balanced (scan time 10.3s) and gradient spoiled (scan time 9.8s) sequences are shown. The image size is 224x224 with resolution of 1.0x1.0x3.0mm$$$^3$$$. Four SVD compressed virtual-coil data are used for reconstruction.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)
3477