3472
Prime Factorizations for Accelerated Radial SC-GROG
Nicholas McKibben1,2 and Edward V. DiBella1,2
1Biomedical Engineering, University of Utah, Salt Lake City, UT, United States, 2Radiology and Imaging Sciences, University of Utah, Salt Lake City, UT, United States
1Biomedical Engineering, University of Utah, Salt Lake City, UT, United States, 2Radiology and Imaging Sciences, University of Utah, Salt Lake City, UT, United States
Synopsis
GROG is an attractive alternative to convolutional gridding and non-uniform DFT methods because of comparatively low cost and no density correction. However, for large multicoil datasets, many fractional matrix powers must be performed which scale with the cube of the number of channels. For SC-GROG and real-time SC-GROG, time and memory requirements can be significantly lowered for precomputation and updates of fractional powers by decomposing required powers into smaller, composable pieces. This is an NP-hard combinatorial change-making problem. We propose a simple solution based on prime factorization which leads to significant computational and memory savings with little performance degradation.
Introduction
Self-calibrating GRAPPA operator gridding (SC-GROG) learns orthogonal GRAPPA operators from multi-channel data without calibration datasets1. It is an attractive alternative to convolutional gridding with comparatively low cost and no density correction. The GRAPPA operators are used to interpolate data onto a Cartesian grid within a small neighborhood and are computed through evaluation of small fractional matrix powers. Complexity of SC-GROG dictionary computation grows as the cube of the number of channels, leading to extended gridding times/memory requirements for datasets with many coils and high resolution2. Real-time strategies have been developed that pre-compute all possible matrix powers, leading to increased memory requirements and higher start-up costs while also requiring calibration data3. We present a method of decomposing the required matrix powers through prime factorizations to find a smaller number of base powers to lower computational cost with comparable performance.Theory
Data is acquired at N k-space locations $$$(k_x, k_y)$$$ which in general do not lie on a Cartesian grid holding M target locations $$$(t_x, t_y)$$$. SC-GROG uses fractional matrix powers of the unit GRAPPA operators usually along the xy-axes to interpolate from acquired data $$$(k_x, k_y)$$$ to the Cartesian grid $$$(t_x, t_y)$$$. We call these unit operators $$$G_j,j \in \{x,y\}$$$ trained from the acquired data as described in1. In the worst case, K=2M unique matrix powers $$$G^i_j$$$ are computed for each acquired point. Semi-regular trajectories, e.g. radial, have repetitions of unique $$$(k_x, k_y)$$$ leading to K<2M. Both training and gridding require expensive computations in the form of iterative or recursive matrix factorizations2.We desire to find the fewest fractional matrix powers to produce the K required $$$G^i_j$$$. This is a modified combinatorial change-making problem: find the denominations of the “coins” (i.e., $$$G^i_j$$$) which lead to the fewest required over all transactions (i.e., minimum K)4. In this problem, we know all transactions, i.e., sampling locations. We can represent this problem mathematically in the form of NP-hard optimizations for $$$G^i_x,G^i_y$$$: $$\text{minimize} || d_j ||_0 + \lambda || y^i_j||_1 \text{ s.t. } p^i_j = (y^i_j)^T d_j$$ where the nonzero entries in $$$d_j \in \mathcal{R}^{2M}$$$ contain the K unique matrix powers, $$$p^i_j$$$ are the 2M $$$\Delta k_j$$$, $$$y^i_j$$$ is an integer column vector indicating how many of each “coin” $$$d_j$$$ is required to achieve all $$$p^i_j$$$. The $$$\ell_0$$$-norm evaluates to K and the minimization is constrained so that all 2M $$$G^i_j$$$ are formed from the minimal K matrix powers, i.e., through chained matrix multiplication. The $$$\ell_1$$$-norm measures the complexity of the composite solution and is penalized for numerical stability of matrix compositions. This problem as stated cannot be solved using standard mixed integer quadratic programming solvers since continuous valued, nonconvex terms involving mixed design variables appear both in the objective and constraints. We therefore propose an approach based on prime factorization. Any number can be uniquely factored into a product of primes: $$A e^{p^i_j} = p_0^{n_0} p_1^{n_1} \cdots$$ $$ p^i_j = n_0 \ln{p_0} + n_1 \ln{p_1} + \cdots - \ln{A} $$ where A is a multiplicative factor that makes the left side of the first equation an integer, n are positive integers, and p are prime factors. Then we have K total prime factors p over all decompositions of $$$p^i_j$$$. For $$$l$$$-place trajectory precision, $$$A \approx 10^l$$$. Thus we only need to compute these K matrix powers to achieve all 2M interpolations.
Methods
Using the algorithm described above, we select the least K operators with which to perform gridding for non-Cartesian datasets. Reconstruction times for radially sampled Shepp-Logan phantoms as well as slices of radially-acquired cardiac perfusion datasets will be compared with the original radial SC-GROG method. As the time required to find prime factorizations of the matrix powers is negligible compared to the time required to compute matrix powers, we expect time savings using the proposed algorithm with little degradation due to increased numerical instability from chained matrix multiplication of small fractional powers.Results
We implemented SC-GROG and the proposed algorithm based on prime factorization in Python1,5. Figure 1 shows a significantly reduced number of fractional matrix powers using the proposed prime factorization method as the number of samples increases. Figure 2 shows the results of the computer simulation with the proposed method performing 4x faster with little error. Figure 3 shows the results of SC-GROG for a perfusion cardiac dataset (72 rays). There is virtually no image degradation, the quality of the main features of the image are maintained, and processing time is >4x faster than standard SC-GROG.Conclusion and Discussion
This method represents an implementation optimization for (real-time) SC-GROG. This technique could be applied to any arbitrary trajectory. The prime factorization algorithm is independent of the number of coil channels and scales only with the number and precision of samples. With known precision, there exists an upper bound on K as there are finitely many prime numbers between 0 and $$$A e^{p^i_j}$$$. K<2M for any non-pathological trajectory. For high precision, tuning is required to select scaling factor A. This method could be effective in real-time systems for initial dictionary computation as well as more frequent weight updates. Future work includes a parallelized implementation of the proposed algorithm and incorporation of multiple scaling factors during integer conversion to reduce numerical instability.Acknowledgements
No acknowledgement found.References
- Seiberlich, Nicole, et al. “Self‐calibrating GRAPPA operator gridding for radial and spiral trajectories.” Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 59.4 (2008): 930-935.
- Higham, Nicholas J., and Lijing Lin. “An improved Schur--Padé algorithm for fractional powers of a matrix and their Fréchet derivatives.” SIAM Journal on Matrix Analysis and Applications 34.3 (2013): 1341-1360.
- Saybasili, Haris, et al. “RT‐GROG: parallelized self‐calibrating GROG for real‐time MRI.” Magnetic resonance in medicine 64.1 (2010): 306-312.
- Wright, J. W. “The change-making problem.” Journal of the ACM (JACM) 22.1 (1975): 125-128.
- Midorikawa, Shiho, primefac, GitHub repository, https://github.com/elliptic-shiho/primefac-fork
Figures

Figure 1: Number of fractional matrix powers required vs number of samples acquired for a radial trajectory. Prime factorization accelerated SC-GROG far outperforms traditional radial SC-GROG in number of required matrix powers.
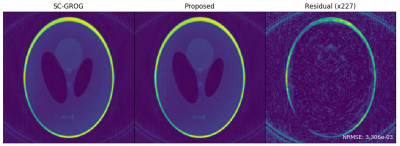
Figure 2: Comparison of traditional SC-GROG and the proposed prime factorization accelerated SC-GROG. The 8-channel Shepp-Logan phantom was radially-sampled (72 rays, 288 samples per ray). The gridded results are virtually identical while the proposed method yields a 4x speed-up of fractional matrix power dictionary precomputation.
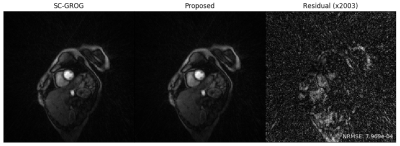
Figure 3: Comparison of traditional SC-GROG and the proposed prime factorization accelerated SC-GROG. The cardiac data was radially sampled (72 rays, 256 samples per ray, 9 channels). The gridded results are again virtually identical with the proposed method yielding a 4.2x speed-up of fractional matrix power dictionary precomputation with negligible error.