3464
Improving cartesian single-shot 2D T2 shuffling and reducing radial streaking artifacts with golden angle radial T2 shuffling1Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 2MR R&D and Collaborations, Siemens Healthineers, Los Angeles, CA, United States, 3Fetal-Neonatal Neuroimaging and Developmental Science Center, Boston Children’s Hospital, Boston, MA, United States, 4Harvard Medical School, Boston, MA, United States, 5Harvard-MIT Health Sciences and Technology, Cambridge, MA, United States, 6Institute for Medical Engineering and Science, Cambridge, MA, United States
Synopsis
T2 shuffling reduces blurring in 3D Fast Spin Echo (FSE) by incorporating a low rank representation of signal evolution in the forward model. However, extending T2 shuffling to 2D-FSE is challenging due to the limited spatiotemporal incoherence achievable with cartesian sampling. Radial trajectories offer increased incoherence in multiple dimensions in comparison to cartesian acquisitions. We combine golden angle radial sampling with the T2 shuffling forward model to improve image quality in comparison to 2D cartesian T2 shuffling and to reduce streaking artifacts in radial single-shot FSE images. Simulation and phantom experiments illustrate the advantages of radial T2 shuffling.
Introduction
Radial trajectories offer improved motion robustness1 and inherent spatial incoherence in comparison to cartesian acquisitions2. However, radial sampling incurs streaking artifacts in T2-weighted fast-spin-echo (FSE) sequences, particularly single-shot-FSE (SSFSE), due to T2-decay during the echo train3.T2 shuffling reduces blurring in 3D-FSE by incorporating a low rank subspace representation of signal evolution in the forward model4. Similar model-based reconstructions have been applied in 3D-radial acquisitions5. However, extending T2 shuffling to 2D-SSFSE is challenging because the limited degrees of freedom in a 2D-cartesian sampling scheme does not yield adequate spatiotemporal incoherence.
We combine Golden Angle radial sampling6 with the T2 shuffling forward model to reduce streaking artifacts in radial SSFSE and improve image quality in comparison to 2D-cartesian single-shot T2 shuffling. We verify the technique in both simulation and phantom studies.
Methods
T2 shuffling Forward ModelConsider a time series of images, $$$x$$$, which represent the object to be imaged at each echo time during a SSFSE acquisition. Signal evolution for realistic T1 and T2 values can be simulated and grouped into a dictionary, which can be well approximated by a basis, $$$Φ$$$, of the dictionary’s left singular vectors. We arrive at the T2-shuffling forward model by projecting $$$x$$$ onto $$$Φ$$$:
$$ y = R F S Φ α$$
Where $$$R$$$ is the spatiotemporal under-sampling mask, $$$F$$$ is the Fourier Transform, $$$S$$$ is the coil sensitivity operator, and $$$α$$$ are the low dimensional coefficients.
Radial Sampling in the T2 shuffling Framework
The T2 shuffling forward model can be altered so that $$$F$$$ represents the non-uniform Fourier Transform and $$$R$$$ encodes the spoke sampled at each echo time. The original T2 shuffling implementation recognized that the $$$F S $$$ and $$$Φ$$$ operators commute, allowing for significant computational benefits4. These operators also commute in the radial case, yielding similar levels of computational speedup.
Experiments
The basis of two singular vectors, corresponding to coefficients $$$α$$$ with dimension 256 x 256 x 2, for all shuffling models were the dominant singular vectors of EPG7 simulated dictionaries of SSFSE signal evolution with a fixed T1 value of 1 s, 160° refocusing pulses, and 50 - 400 ms T2-range.Point Spread Function Experiment
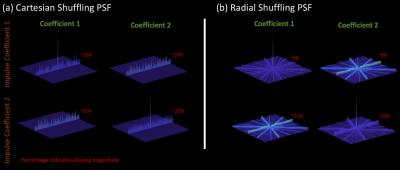
Two point spread functions for both trajectories were computed by passing a centered unit impulse, in either the first or second coefficient, through the appropriate forward and adjoint shuffling operator. The radial SSFSE acquisition model incorporated a golden angle sampling scheme with 80 radial spokes. The cartesian SSFSE model consisted of 80 evenly spaced (including 24 calibration), temporally shuffled phase encode lines. Both models had an echo spacing of 5 ms and utilized single channel, uniform coil sensitivity.
Numerical Experiment
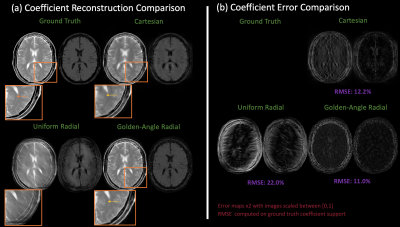
We obtained T1, T2, proton density, and coil sensitivity maps from the brainweb database8. We aimed to compare radial shuffling to both cartesian T2 shuffling and a radial l1-regularized SENSE reconstruction. Cartesian SSFSE acquisitions were simulated with 80 temporally shuffled, uniformly spaced phase encode lines and an echo spacing of 5 ms. Radial SSFSE acquisitions were simulated with 80 spokes, an echo spacing of 5 ms, and both a uniform and golden angle reordering scheme. The FOV, resolution, and matrix size was 256 x 256 mm, 1 x 1 mm, 256 x 256 for all acquisitions.
Phantom Experiment
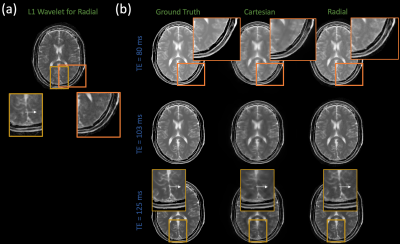
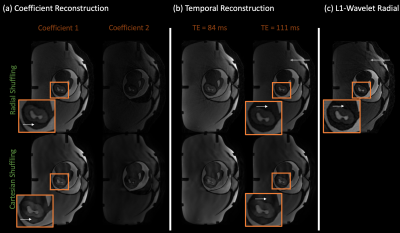
A pregnant abdomen phantom was scanned on a 3T Siemens Skyra with a temporally shuffled, uniformly spaced 99 (including 24 calibration) phase encode point cartesian SSFSE acquisition and a prototype Radial FSE sequence with 76 spoke golden angle reordering. The cartesian and radial sequences had echo spacings of 5.56 ms and 8 ms respectively. The FOV, resolution, slice thickness, and matrix size was 300 x 300 mm, 1.17 x 1.17 mm, 3 mm, and 256 x 256 respectively for both acquisitions. Sensitivity maps were generated from a calibration scan using ESPIRiT9.
Reconstruction Details
All T2 shuffling and l1-SENSE problems were solved with BART10. Cartesian shuffling and SENSE utilized a l1-wavelet prior while radial shuffling incorporated no regularization.
Results
Figure 1 compares the point spread functions between golden angle radial and cartesian shuffling. In all cases, the golden angle radial trajectory achieves at least a 2x improvement in aliasing magnitude, implying a better posed shuffling problem. Figure 2 compares temporal coefficients from the cartesian, uniform radial, and golden angle radial numerical experiments with associated error maps. Figure 3 compares the time series of images computed from the cartesian and golden angle coefficients, seen in Figure 2, with the l1-SENSE golden angle radial reconstruction. Radial shuffling achieves the lowest coefficient root-mean-square-error values, improves the image quality of the cartesian shuffling coefficients and temporal images, and reduces streaking artifacts seen in the non-shuffling radial reconstruction. Figure 4 compares coefficient and temporal reconstructions between cartesian shuffling, radial shuffling, and l1-SENSE radial from the phantom experiment. Radial shuffling reduces the aliasing and streaking artifacts seen in the other two techniques.Discussions and Conclusions
We combined golden angle radial trajectories with the T2 shuffling forward model. Numerical simulations and phantom experiments demonstrate the potential of the technique to improve cartesian T2 shuffling and reduce radial streaking artifacts. In-vivo experiments are required to understand performance changes in realistic imaging scenarios due to effects like B0 inhomogeneity.Acknowledgements
This work was supported in part by research grants NIH R01 EB017337, U01 HD087211, R01HD100009, the NVidia Corporation for computing support, and support from the Skolkovo Institute of Science and Technology Next Generation Program. In addition, this material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. 1122374. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.References
1. Zaitsev M, Maclaren J, Herbst M. Motion artifacts in MRI: A complex problem with many partial solutions. J Magn Reson Imaging. 2015;42: 887–901.
2. Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magn Reson Med. 2007;57: 1086–1098.
3. Theilmann RJ, Gmitro AF, Altbach MI, Trouard TP. View-ordering in radial fast spin-echo imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2004;51: 768–774.
4. Tamir JI, Uecker M, Chen W, Lai P, Alley MT, Vasanawala SS, et al. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn Reson Med. 2017;77: 180–195.
5. Keerthivasan MB, Saranathan M, Johnson K, et al. An efficient 3D stack‐of‐stars turbo spin echo pulse sequence for simultaneous T2‐weighted imaging and T2 mapping. Magn Reson Med. 2019;82:326–341.
6. Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE Trans Med Imaging. 2007;26: 68–76.
7. Weigel M. Extended phase graphs: dephasing, RF pulses, and echoes‐pure and simple. J Magn Reson Imaging. 2015.
8. Collins DL, Zijdenbos AP, Kollokian V, Sled JG, Kabani NJ, Holmes CJ, et al. Design and construction of a realistic digital brain phantom. IEEE Trans Med Imaging. 1998;17: 463–468.
9. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014;71: 990–1001.
10. Tamir JI, Ong F, Cheng JY, Uecker M, Lustig M. Generalized magnetic resonance image reconstruction using the Berkeley Advanced Reconstruction Toolbox. ISMRM Workshop on Data Sampling & Image Reconstruction, Sedona, AZ. 2016.
Figures