3462

Contrast prediction-based regularization for iterative reconstructions (PROSIT)

Hendrik Mattern¹, Alessandro Sciarra^1,2, Max Dünnwald^2,3, Soumick Chatterjee^1,3,4, Ursula Müller¹, Steffen Oeltze-Jafra^2,5, and Oliver Speck^1,5,6,7
¹Biomedical Magnetic Resonance, Otto-von-Guericke University, Magdeburg, Germany, ²Medicine and Digitalization, Otto-von-Guericke University, Magdeburg, Germany, ³Faculty of Computer Science, Otto-von-Guericke University, Magdeburg, Germany, ⁴Data & Knowledge Engineering Group, Otto-von-Guericke-University, Magdeburg, Germany, ⁵Center for Behavioral Brain Sciences, Magdeburg, Germany, ⁶German Center for Neurodegenerative Disease, Magdeburg, Germany, ⁷Leibniz Institute for Neurobiology, Magdeburg, Germany

Synopsis

In this study, contrast prediction is used as an auxiliary tool to regularize underdetermined image reconstructions. This novel regularization strategy enables to share information across individual reconstructions and outperforms state of the art regularizations for high acceleration factors.

Introduction

Compressed sensing¹ in combination with parallel imaging has been applied to speed up the inherently slow data acquisition of MRI². Estimating an image from undersampled data requires solving an underdetermined system often formulated as a minimization problem³:
$$ \underset{x}{\mathrm{arg min}} \frac{1}{2} \parallel Ax - y \parallel^2_2 + \frac{\lambda}{2} \Psi (x) $$
The first term enforces data consistency (with A-encoding matrix, x–reconstructed image, y–undersampled k-space) while the second term is used for regularization. Common regularization strategies include total variation(TV) and L1-norm on the wavelet transformed image(L1WT).
These regularizations do not leverage potentially available information from other scans. By applying deep learning-based contrast prediction, the image to be acquired can be approximated from a previously acquired contrast⁴.
In this study, image prediction is used for regularization to share information across contrasts. Rather than replacing data acquisition, image prediction is used within the reconstruction. This could address the concern that image prediction itself might not faithfully depict all contrast-specific image details.

Methods

Using SigPy⁵ PRedictiOn-baSed regularIzaTion (PROSIT) was implemented and compared to TV and L1WT reconstructions. Similarity between prediction p and reconstruction x was enforced by L2-norm:
$$ \underset{x}{\mathrm{arg min}} \frac{1}{2} \parallel Ax - y \parallel^2_2 + \frac{\lambda}{2} \parallel x-p \parallel^2_2 $$
From the undersampled data (Variable-density Poisson-disk patterns, 24x24 calibration region), sensitivity maps were estimated using ESPIRiT⁶.

Phantom study: Impact of the prediction on the reconstruction

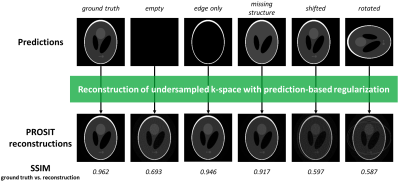
How different predictions effect PROSIT reconstruction quality was investigated in a phantom study (python script publicly available⁷). A 4-channel Shepp-Logan phantom with 16-fold undersampling was simulated. Besides the ground truth, several deliberately corrupted priors were generated and used for regularization: empty image, 10-voxel shifted, 90°-rotated, edge only, and missing central structure (see Fig.1). Ground truth and reconstructions were compared using SSIM values⁸.

Brain study: Comparison of different regularization strategies
A conditional adversarial network⁹ was trained to predict T1-weighted, T2-weighted, and FLAIR images from PD-weighted images. Prior to each prediction, the channel-combined, defaced images were co-registered and interpolated to 0.5x0.5x1.2mm voxel-size. Further details are provided in¹⁰(see “RePro” dataset).
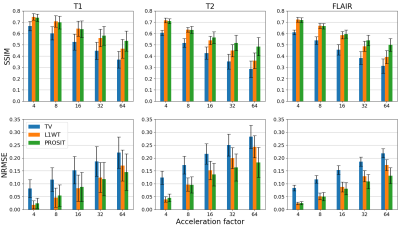
In total, 300 slices with prediction and ground truth were available (100 slices for each contrast). For each slice, 4 channels were simulated and k-space was undersampled 4-, 8-, 16-, 32, or 64-fold. SSIM and NRMSE were used to assess reconstruction performance using PROSIT, TV, and L1WT regularization (lambda 0.01, 0.0001, and 0.0001, respectively; individual tuning of each regularization using SSIM; 30 iterations).
Dependency of PROSIT reconstruction on contrast prediction quality was assessed qualitatively for a single slice and quantitatively for all datasets by correlating SSIM and NRMSE values.

Results

Phantom study
Conditioning the reconstruction with a ground truth results in superior image quality (SSIM=0.962, see Fig.1). Compared to a perfect prediction, an empty prior lowers SSIM outcome by 28% and is equivalent to enforcing an L2-norm on the reconstructed image itself. Edge-only prediction induced mild blurring (-2% SSIM). Omitting the central structure introduced an additional spike to the image center (-5% SSIM). Nevertheless, the missing structures in the prediction could be recovered in the PROSIT reconstruction. Thus, imperfect prediction was partially corrected during the reconstruction. Misalignment of prediction and reconstruction resulted in artifacts and reduced reconstruction quality (-38% for translation; -39% for rotation).

Brain study
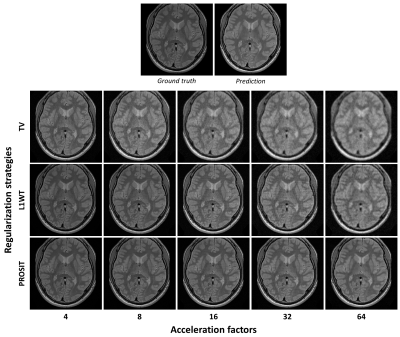
Comparison of the three regularizations for 4 to 64-fold undersampling are shown in Fig.2&3. Compared to the 4 simulated channels, the acceleration factors used were ambitious. In general, residual undersampling artifacts and blurring increased with higher acceleration factors, but the level of image degradation depended on the regularization used. In this study, TV is inferior to the other regularization strategies regardless of the undersampling (see Fig.2&3). PROSIT outperforms L1WT with increasing acceleration factor (on average 25% and 22% improved SSIM and NRMSE for 64-fold undersampling across all contrasts). For T2-weighted and FLAIR data, PROSIT outperformed L1WT for acceleration factors$$$\geq$$$16 and for T1-weighted images for accelerations factors$$$\geq$$$32. L1WT has a quantitative advantage over PROSIT for less ambitious undersampling (1% in SSIM, 16% NRMSE for 4-fold acceleration on average over all contrasts), although visually both regularizations seem to be on par.
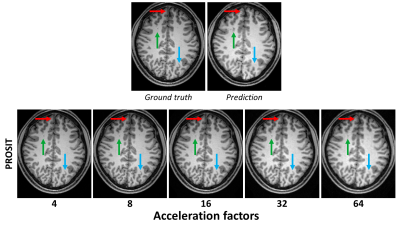
Correlation between PROSIT reconstruction and prediction quality increased for higher acceleration factors (see Fig.4). Although, higher acceleration factors increase the likelihood of propagating prediction errors into the reconstructed image, anatomical features are largely preserved even for 64-fold undersampling with imperfect prior knowledge (see Fig.5).

Discussion

Contrast prediction can be leveraged to regularize underdetermined reconstructions. For high accelerations factors, prediction-based regularization outperformed TV and L1WT regularization, and the reconstruction quality correlated stronger with the prediction quality. In the future, improving contrast prediction should improve PROSIT reconstruction quality further.
Like with any prior, regularization with PROSIT could compromise image details or introduce artificial structures. However, this inherent problem of contrast prediction is reduced in the context of regularization as real measured data is included in the image generation. To analyze (over-)regularization in more detail, further tests are required, ideally, with native multi-channel data including pathologies.

Conclusion

A novel method to share information across contrasts and reconstructions was presented. By leveraging contrast prediction in regularized reconstructions, the benefits of both techniques can be combined while inherent challenges of image prediction are partially migrated and very high undersampling factors can be achieved.

Acknowledgements

This work was supported by the NIH, grant number 1R01-DA021146; the federal state of Saxony-Anhalt under grant number ‘I 88’ (MedDigit); and was in part conducted within the context of the International Graduate School MEMoRIAL at OvGU (project no. ZS/2016/08/80646).

References

1. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182–1195. doi: 10.1002/mrm.21391.

2. Feng L, Grimm R, Block KT, Chandarana H, Kim S, Xu J, Axel L, Sodickson DK, Otazo R. Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med. 2014;72(3):707–717. doi: 10.1002/mrm.24980.

3. Fessler JA. Optimization methods for MR image reconstruction; 2019. Available from: http://arxiv.org/pdf/1903.03510v1.

4. Dar SU, Yurt M, Karacan L, Erdem A, Erdem E, Cukur T. Image Synthesis in Multi-Contrast MRI With Conditional Generative Adversarial Networks. IEEE Trans Med Imaging. 2019;38(10):2375–2388. doi: 10.1109/TMI.2019.2901750.

5. https://sigpy.readthedocs.io/

6. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990–1001. doi: 10.1002/mrm.24751.

7. https://gitlab.com/hmattern/tmi/tree/master/PROSIT

8. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing. 13 (4) doi:10.1109/TIP.2003.819861.

9. Isola P, Zhu JY, Zhou T, Efros AA. Image-to-Image Translation with Conditional Adversarial Networks. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). doi: 10.1109/CVPR.2017.632

10. Sciarra A, Dünnwald M, Kaufmann J, Schreiber S, Oeltze-Jafra S. Multi-contrast MR Brain Image Synthesis: From Single to Multiple Prediction and Vica Versa. Submitted for review.

Figures

Figure 1: Influence of different predictions on PROSIT reconstructions.

Figure 2: A single T2-weighted slices is shown for qualitative comparison of different regularization strategies for 4 to 64-fold acceleration.

Figure 3: Quantitative assessment of different regularization strategies by SSIM and NRMSE. Results for T1-weighted, T2-weighted, and FLAIR reconstructions are reported separately.

Figure 4: Correlation of prediction vs. PROSIT reconstruction quality with respect to the ground truth. Data points are color-coded according to the underlying contrast. Correlation is computed across contrasts and increases for higher acceleration factors.

Figure 5: Qualitative evaluation of error propagation induced by imperfect predictions for a single T1-weighted slice. A structured noise artifact in the prediction (red arrow) is gradually added to the reconstruction with increasing undersampling. Propagation of false anatomical features in the prediction (blue and green arrow) is largely prevented.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3462