Introduction

One prominent application of quantitative susceptibility mapping (QSM) is quantifying brain iron alterations in Parkinson’s Disease (PD) patients[1,2]. PD patients commonly exhibit tremor symptoms, which inevitably causes motion artifacts that degrade the quality and accuracy of QSM images. In our experience, over 30% of routine clinical scans of PD patients are significantly corrupted by motion. Developing an algorithm that can reduce the motion artifacts in QSM is thus highly desirable.

QSM is calculated through deconvolving the gradient-echo MRI phase signal by the magnetic dipole kernel[3,4], which is prone to noise amplification due to the under-determined nature of the dipole kernel. Various regularization methods[5,6,7,8,9] have been adopted to improve the QSM quality; however, none of these are able to suppress motion artifacts. Here, we explore the utility of dictionary learning to regularize QSM reconstruction for motion artifact reduction. The rationale is that the reconstruction projects the data onto a leant dictionary that rejects motion artifacts so as to achieve the reduction of motion artifacts.

Methods

Problem formulation
A typical formulation of QSM reconstruction is the following, $$ \chi = \min_\chi \; \lVert W\cdot(\phi-F^\ast D \cdot F \chi)\rVert + R(\chi,W) \;\;\;\;\;\;\;\;\;\;[1] $$
where $$$\phi$$$ is the normalized tissue phase, $$$D$$$ is the three-dimensional magnetic dipole kernel, $$$F$$$ is Fourier transform, "$$$\ast$$$" denotes the adjoint of a transform, and “$$$\cdot$$$” represents element-wise multiplication. $$$R(\chi, W)$$$ can be any form of regularization.

The dictionary learning approach assumes the susceptibility map can be sparsely represented by a dictionary as illustrated in Figure 1. The inverse problem states as (P0) \begin{equation}\text{(P0):} \;\;\;\;\;\;\;\;\;\;\begin{aligned} {\chi, \Lambda,L} =\arg \min_{\chi, \Lambda,L} \;\; &\lVert \phi-F^\ast D \cdot F \chi\rVert_2^2+\rho \lVert P \chi - L \Lambda \rVert_F^2\\ \text{s.t.}\;\; &\lVert \Lambda(:,i) \rVert_1 < T_0 , \;\;\forall i\end{aligned} \;\;\;\;\;\;\;\;\;\; [2]\end{equation}
The first term ensures data fidelity according to the QSM physical model. The second term is the cost function tracking the quality of sparse approximated image. $$$P$$$ represents the operation to extract patches with maximum overlap. $$$L$$$ is the dictionary in which each column is one vectorized atom. Each column of $$$\Lambda$$$ is the sparse representation for corresponding vectorized image patch. $$$T_0$$$ provides adjustment to the sparsity level.

Algorithm
(P0) can be solved as 2 sub-problems.
$$\text{(P0-1):} \;\;\;\;\;\;\;\;\;\; {\Lambda,D} =\arg \min_{\Lambda,D} \;\; \lVert P \chi - L \Lambda\rVert_F^2+\lambda \sum_i \lVert\Lambda(:,i) \rVert_1 \;\;\;\;\;\;\;\;\;\;[3]$$
The dictionary is learnt to sparsify the susceptibility map $$$\chi$$$ which is initialized with the truncated k-space division (TKD) method[10]. The atoms are then initialized with random image patches from the TKD QSM image and trained using an $$$l_1$$$-relaxed KSVD-like algorithm. In an alternating fashion, at each iteration, sparse representation is found using ADMM method[11], and the dictionary is updated column by column while ensuring maximal incoherence of atoms.

The learnt dictionary is then used to sparsify the image as a regularization as follows$$\text{(P0-2):} \;\;\;\;\;\;\; \chi =\arg \min_{\chi} \;\; \lVert \phi-F^\ast D \cdot F \chi\rVert_2^2 +\rho \lVert P \chi - L \Lambda \rVert_F^2\ \;\;\;\;\;\;\;\;\;\;[4]$$
The solution of (P0-2) should satisfy the Karush–Kuhn–Tucker (KKT) condition which states,
$$F^\ast D^2 \cdot F \chi +\rho \chi = F^\ast D \cdot F \phi + \rho PL\Lambda \;\;\;\;\;\;\;\;\;\;[5]$$
Rearranging terms yields,
$$(D^2 +\rho \mathbf{1}) \cdot F \chi = D \cdot F \phi + \rho F P^\ast L\Lambda \;\;\;\;\;\;\;\;\;\;[6]$$
$$\chi = F^\ast \; (\frac{D \cdot F \phi + \rho F P^\ast L\Lambda}{D^2 +\rho \mathbf{1}}) \;\;\;\;\;\;\;\;\;\;[7]$$
where $$$\mathbf{1}$$$ is all-ones matrix in proper dimensions. Note that $$$P^\ast$$$ contains an averaging step for the overlapped area of patches.

Experiments
The multi-echo GRE data was acquired on a GE MR 750 3T scanner with the following parameters: spatial resolution = $$$0.4\times 0.4 \times 2 \;\text{mm}^3$$$, image size = $$$512 \times 512 \times 64 $$$, TR = $$$33.8 \; \text{ms}$$$, echo numbers = $$$8$$$, TE1 = $$$4.6 \; \text{ms}$$$, echo spacing = $$$3.6 \; \text{ms}$$$, FA = $$$20^{\circ}$$$. Image patch size was $$$6 \times 6$$$. Dictionary was set to have 100 atoms and trained with 1000 image patches for 50 iterations. STAR-QSM[8] in STIsuite[12] was performed for quality comparison.

Results

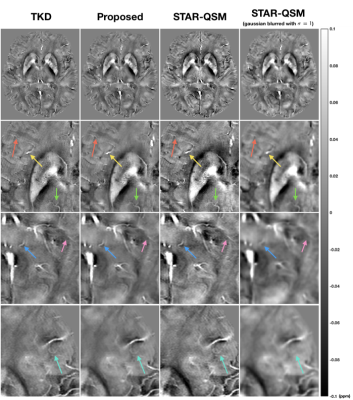
Dictionary learning session converges with only 50 iterations (Figure 1). Figure 2 compares the proposed sparse-coding regularized method with TKD and STAR-QSM. The proposed method reduces the motion-induced ringing artifacts while preserving the veins and other sharp structures. The reduction of the motion artifacts is not a result of simple spatial smoothing as demonstrated by the comparison with gaussian-blurred STAR-QSM results. The latter blurs structural details that are preserved in the proposed method.

While TKD results were used as the initialization in learning the dictionary, the proposed method resolves the underestimation issue and reduces the streaking artifacts as shown in simulation (Figure 3).

A globally learnt dictionary pre-trained from a database of QSM images can also be utilized in the regularization. The difference in the resulting images from adaptively and globally learnt dictionary is very minimal (Figure 4).

Conclusions

This work employs sparse dictionary learning to regularize QSM image reconstruction, which can be concurrently applied with other regularizations. The proposed method provides a way to rescue motion-corrupted images acquired in clinical settings where re-scanning the patient is costly or impractical. Nonetheless, further validations on phantom experiments and on more diverse patients/subjects are needed to verify the accuracy and robustness.

Acknowledgements

No acknowledgement found.