3458
Low-Rank Tensor Completion for Accelerated Magnetic Resonance Imaging
Shen Zhao1, Lee C. Potter1, and Rizwan Ahmad2
1Department of Electrical and Computer Engineering, The Ohio State University, Columbus, OH, United States, 2Department of Biomedical Engineering, The Ohio State University, Columbus, OH, United States
1Department of Electrical and Computer Engineering, The Ohio State University, Columbus, OH, United States, 2Department of Biomedical Engineering, The Ohio State University, Columbus, OH, United States
Synopsis
We present a method for calibration-less, accelerated Magnetic Resonance Imaging (MRI) via canonical polyadic decomposition (CPD) based low-rank tensor completion (LRTC). LRTC exploits the higher dimensional structure inherent in MRI. Preliminary results show that LRTC can outperform structured low-rank matrix completion methods for 2D and compressed sensing-based methods for dynamic applications.
Introduction
Recently, several low-rank matrix completion methods have been proposed to recover unobserved k-space samples. These methods do not require auto-calibration signal (ACS) region and thus can facilitate higher acceleration rates [2,3,4]. The recent advancements in multi-linear algebra techniques have led to unprecedented performance for many signal processing problems, including data compression, pattern recognition, and prediction. MRI data essentially resides in three or more dimensions, including spatial encodings, receive coils, time, and velocity encoding. We utilize a multi-linear algebra tool, namely LRTC, instead of traditional linear algebra tools to fully exploit the rich, high-dimensional structure in MRI data.Methods
For calibration-less 2D MRI, SAKE, P-LORAKS, and ALOHA exploit low-rank property of a "data matrix", which is the concatenation of the block Hankel matrices, one from each coil. However, this requires flattening the underlying tensor into a structured 2D matrix. Since the mapping from a tensor to a matrix is not unique, it is not clear if a single flattening convention can fully exploit the high-dimensional data structure. In contrast, we explicitly build a tensor that is a stack of block Hankel matrices and do not perform any flattening. An illustration of different arrangements of block Hankel matrices is shown in Figure 1. For 2D+t MRI, we can simply stack the structured 3D tensor for each frame along the time dimension to build a 4D tensor. However, due to the large memory footprint of the LRTC processing, we partially flattens the 4D tensor by concatenating coil dimension horizontally (see Figure 1), resulting in a 3D tensor. We transformed the MRI reconstruction problem into a structured low-rank tensor completion problem, given as$$ \min \text{rank} \{\text{S}(D)\},\\
\text{subject to } D\circ M = D_o$$
where $$$\text{S}$$$ denotes the transformation from the k-space tensor to a structured tensor. For 2D, $$$\text{S}(D)$$$ is the stack of block Hankel matrices, one from each coil. For 2D+t, $$$\text{S}(D)$$$ is the stack of ``data matrix'', one from each frame (2D+t). Here, $$$D$$$ is the k-space data tensor, $$$\circ$$$ represents element-wise multiplication, $$$M$$$ is the sampling pattern, and $$$D_o$$$ is the observed k-space with zero filling.
To solve the LRTC problem, we perform alternating projections onto the subspaces of the stack of block Hankel matrix, low-rank tensor, and data consistency via CPD and CPD-based LRTC. For each step, we update the underlying CPD basis vectors instead of unobserved k-space samples. For implementation, we use the ``cpd'' function with respect to incomplete and dense tensor from tensorlab toolbox [5]. The implementation of LRTC is depicted in Figure 2.
Results and Discussion
We retrospectively downsampled an 8-coil 2D brain dataset with random sampling at acceleration rate $$$R=3$$$. The tuning parameters for each method were fined-tuned using an additional dataset (not shown). For all methods, we fixed the maximum number of iterations to be 200, and set the stopping tolerance, i.e., relative change in the entire k-space, to be $$$10^{-3}$$$. For 2D, we compared LRTC with P-LORAKS and SAKE. The results are summarized in Figure 3. LRTC outperforms other methods by more than 3 dB in terms of k-space reconstruction SNR.For 2D+t, we retrospectively downsampled 1.5T cardiac cine data using random Cartesian sampling with undersampling only in the phase-encoding direction. We manually tuned parameters for all methods using an additional dataset at acceleration rate 4. The reconstruction SNR for different methods at different acceleration rates is in Figure 5, and a representative frame of reconstruction is in Figure 4. LRTC has the highest reconstruction SNR for $$$R\leq 8$$$. Figure 4 shows representative frames at $$$R=4$$$.
Conclusion
We have presented an LRTC method for MRI reconstruction. The method is validated using 2D data from brain imaging and dynamic data from cardiac cine. LRTC outperforms state-of-the-art in terms of image quality and presents an emerging avenue for calibration-less reconstruction.Acknowledgements
This work was funded by NIH R01HL135489.References
- C. Chen, Y. Liu, P. Schniter, N. Jin, J. Craft, O. Simonetti, and R. Ahmad, “Sparsity adaptive reconstruction for highly accelerated cardiac mri,” Magn. Reson. Med, vol. 81, no. 6, pp. 3875–3887, 2019.
- J. P. Haldar and J. Zhuo, “P-LORAKS: Low-rank modeling of local k-space neighbor- hoods with parallel imaging data,” Magn. Reson. Med, vol. 75, no. 4, pp. 1499–1514, 2016.
- K. H. Jin, D. Lee, and J. C. Ye, “A general framework for compressed sensing and par- allel MRI using annihilating filter based low-rank hankel matrix,” IEEE Trans Comp. Imag., vol. 2, no. 4, pp. 480–495, 2016.
- P. J. Shin, P. E. Larson, M. A. Ohliger, M. Elad, J. M. Pauly, D. B. Vigneron, and M. Lustig, “Calibrationless parallel imaging reconstruction based on structured low- rank matrix completion,” Magn. Reson. Med, vol. 72, no. 4, pp. 959–970, 2014.
- N. Vervliet, O. Debals, L. Sorber, M. Van Barel and L. De Lathauwer Tensorlab 3.0, Available online, Mar. 2016. URL: https://www.tensorlab.net/
Figures
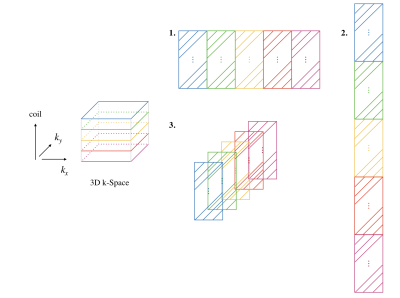
Figure 1: Illustration of stacking vs. flattening of the block Hankel matrices. Given a
2D kernel size, we build a block Hankel matrix for each coil. For LRTC, those matrices are stacked (3), while in matrix completion methods those matrices are concatenated
horizontally (1) or vertically (2).
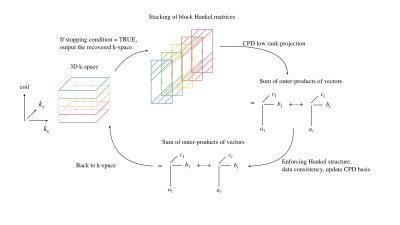
Figure 2: Visual depiction of the LRTC implementation for 2D parallel imaging. Starting with zero-filled 3D k-space, build the stack of block Hankel matrices. Inside each iteration, (i) perform CPD to get a low rank approximation basis $$$\{a_i\}_1^r, \{b_i\}_1^r,\{c_i\}_1^r$$$, (ii) update $$$\{a_i\}_1^r, \{b_i\}_1^r,\{c_i\}_1^r$$$ based on the data consistency and block Hankel structure, and (iii) check the relative change in k-space against the stopping criterion.
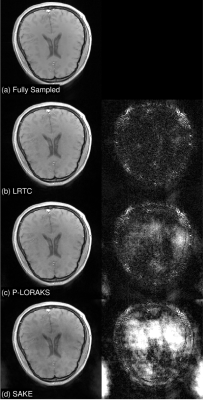
Figure 3: Representative 2D reconstruction results. The coil combined images (left) and 10$$$\times$$$ the absolute differences (right). The k-space reconstruction SNR for LRTC, P-LORAKS, and SAKE are 24.08 dB, 20.76 dB, and 14.85 dB.
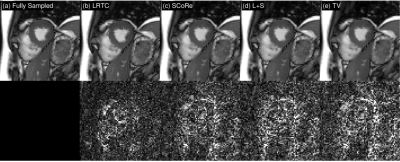
Figure 4: Representative frames from cine reconstruction. Coil combined images (top row) and 20$$$\times$$$ the absolute differences (bottom row). The k-space reconstruction SNR for LRTC, SCoRe [1] , L+S and TV are 25.43 dB, 24.44 dB, 24.14 dB, and 23.85 dB.
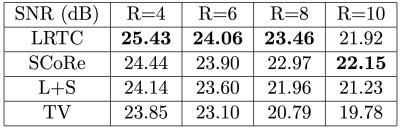
Figure 5: 2D+t reconstruction comparison. The k-space reconstruction SNR for LRTC and three compressive sensing reconstructions are given for $$$R=4, 6, 8, 10$$$