Introduction

Sparse representation of signals using a linear combination of dictionary atoms is a popular choice in regularizing MR image reconstruction. Data-driven dictionary learning has often shown to provide better results than hand-crafted dictionaries in Compressed Sensing(CS)-MRI^[1,5]. Data-driven dictionaries are either learned in a 'supervised' fashion from training images obtained from fully sampled k-space measurements, and then used to reconstruct images from undersampled k-space measurements, or are learned assuming knowledge of only the undersampled k-space measurements, and hence dubbed 'blind'.

This work investigates combining supervised and blind learning of patch-based dictionaries for image reconstruction, especially when very limited fully sampled data is available for supervised training. We represent the image being reconstructed jointly using two dictionaries^[2]: one learned from uncorrupted data, and one in a semi-blind fashion, combined in a residual manner. We also 'tailor' the supervised learning to the undersampled image being reconstructed using a block matching operation. Including a supervised dictionary should boost image quality when blind dictionary learning alone is insufficient.

Methods

Given $$$y\in\mathbb{C}^p$$$, an undersampled k-space measurement vector, $$$T\in\mathbb{C}^{n\times N_1}$$$ a matrix of$$$~N_1$$$ vectorized patches (as columns) from a few images obtained from fully sampled k-space measurements, and $$$\hat{x}$$$ an image being reconstructed from $$$y$$$, the proposed reconstruction approach alternates between solving the following sub-problems:

• Block-Matching (For each patch in$$$~\hat{x}$$$, find the best matching patch in the training data$$$~T$$$ ):

$$(P0)\qquad S=\big[S_1,\ldots,S_j,\ldots,S_{N_2}\big]$$

where$$S_j=\tau_j(T,\mathcal{P}_j\hat{x})=T_{\hat{i}(j)},\qquad\hat{i}(j)=\underset{i\in\{1,...,N_1\}}{\text{arg}~\text{min}}\|H_{\lambda_0}\bigg(W\big(T_i-\mathcal{P}_j\hat{x}\big)\bigg)\|_2^2,$$
$$$\mathcal{P}~$$$extracts$$$~(\sqrt{n}\times\sqrt{n})~$$$patches from an image as a vector and places them as columns of a matrix with $$$\mathcal{P}\hat{x}\in\mathbb{C}^{n\times N_2}$$$,$$$~W\in\mathbb{C}^{n\times n}~$$$is a DCT matrix,$$$~H_{\lambda}(\cdot)$$$ is the hard-thresholding operator, $$$j~$$$indexes the columns of $$$S,\mathcal{P}\hat{x}\in\mathbb{C}^{n\times N_2}$$$, and $$$i~$$$indexes the columns of$$$~T$$$. We applied DCT hard-thresholding before non-local block-matching to reduce the influence of aliasing artifacts on the results.

• Supervised Dictionary Learning (learn a dictionary$$$~\hat{D}_1~$$$from the selected training patches):

$$(P1)\qquad\hat{D}_1=\underset{D_1}{\text{arg}~\text{min }}\underset{Z_3}{\text{min }}\|S-D_1Z_3\|_F^2+\lambda_3^2\|Z_3\|_0\qquad\text{s.t.}~\|(d_1)_j\|_2=1~\forall~j,$$
where $$$(d_1)_j$$$ is the $$$j$$$th column of the supervised dictionary $$$D_1\in\mathbb{C}^{n\times J_1}$$$, $$$Z_3\in\mathbb{C}^{J_1\times N_2}$$$ is a matrix of sparse codes, and $$$\lambda_3$$$ is a regularization parameter.

• Semi-Blind Residual Dictionary Learning and Image Update:

$$(P2)\qquad\hat{x}=\underset{x}{\text{arg}~\text{min }}\underset{D_2,Z_2,Z_1}{\text{min }}\nu\|F_ux-y\|_2^2+\|\mathcal{P}x-\hat{D}_1Z_1-D_2Z_2\|_F^2+\lambda_1^2\|Z_1\|_0+\lambda_2^2\|Z_2\|_0\qquad\text{s.t.}~\|(d_2)_j\|_2=1~\forall~j,$$
where $$$F_u$$$ is the undersampled Fourier encoding matrix, $$$(d_2)_j~$$$is the $$$j$$$th column of $$$D_2\in\mathbb{C}^{n\times J_2}$$$, and $$$Z_1\in\mathbb{C}^{J_1\times N_2}$$$, $$$Z_2\in\mathbb{C}^{J_2\times N_2}$$$ are matrices of sparse codes, and $$$\lambda_1,\lambda_2$$$ are regularization parameters.

Effectively, we learn a blind dictionary to fit the residual of the supervised dictionary representation of the aliased image patches. Once the image $$$\hat{x}$$$ is updated, We repeat the steps $$$P0-P2$$$ as an outer iteration, as shown in Fig 1, to iteratively refine the image and the Super-BReD model.

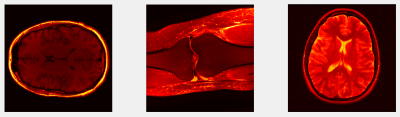
We use overlapping patches from three fully-sampled complex images depicted in Fig 2 as our training data. The updates in $$$P1$$$ and $$$P2$$$ are done in a highly efficient block-coordinate descent fashion similar to [3]. We test our methods for reconstructing two T1-weighted complex brain images and two knee images^[4] (simulated single-coil) retrospectively undersampled at 4x and 5x acceleration factors using variable density masks (brain) and phase-encode lines (knee). We compared our method to the recent state-of-the-art SOUP-DIL^[3] algorithm, which uses blind dictionary learning and has been shown to provide competitive performance in CS-MR image reconstruction.

For our experiments, we used$$$~n$$$=36,$$$J_1$$$=50, and $$$J_2$$$=144. We set$$$~\lambda_1=\lambda_2=\lambda_3=\lambda$$$, and $$$\lambda_0=\lambda/2$$$ in each outer iteration, and $$$\lambda$$$ decreased in log-space between 0.35-0.04^[3] across 75 outer iterations. 5 inner iterations for dictionary learning and sparse coding was used in$$$~P1~$$$and$$$~P2$$$. For fairness, SOUP-DIL also used the same number of inner and outer iterations, and 144 unsupervised atoms. Both algorithms were initialized with a zero-filled reconstruction and overcomplete inverse DCT dictionaries.

Results

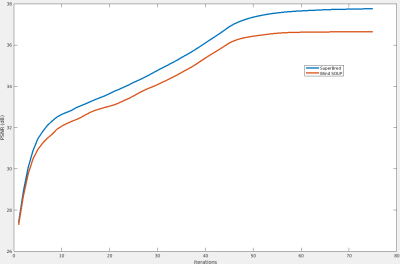
From the table in Fig 3, it is evident that including the supervised dictionary provides significant PSNR gains (0.2-1.1 dB) across most test cases, in both 4x and 5x undersampling. The error maps in Fig 4 show that in the reconstructed brain images, a lot of the improvements were in regions in the skull, which explains the very high PSNR gains from Super-BReD, whereas there are other regions where the details were more clearly preserved for the proposed methods than blind SOUP-DIL. This observation hints at the proposed method's potential for faithful reconstruction of patterns in the data common to both training and test. These improvements can partially be attributed to the supervised block-matching. For the reconstructed knee images as well, we see significant PSNR gains using our method and more fidelity with the ground truth in the finer details, as indicated with arrows. Fig 5 shows that Super-BReD leads to higher gains in PSNR over iterations than blind SOUP-DIL.

Conclusion

We investigated combining supervised and blind dictionary learning for CS-MRI. Our preliminary results indicate that, even without careful tuning of hyperparameters, Super-BReD learning provides better image quality than blind dictionary learning. Our proposed method allows for tailoring of supervised learning with blind learning via a block matching step, and presents a novel approach for incorporating supervision in model-based image reconstruction in the presence of limited training data.

Our future work will involve comparison to other machine learning methods, and application to multi-coil MR image reconstruction as well as dynamic MRI, where high-quality training data is typically unavailable. Given the direct connection between deep-learning and dictionary learning^[6], we also plan to explore incorporating the proposed ideas in such generalized dictionary learning.