Introduction

Recently, four-dimensional (4D) MRI has become an emerging developmental technique in radiotherapy treatment planning. However, long scanning time and motion artifacts remain the major barriers preventing the further implementation of 4D-MRI in clinic. With the introduction of compressed sensing, many reconstruction approaches have been proposed for accelerated MRI by exploiting the sparsity in the transform domain. Total variation (TV) regularization scheme has been widely applied in high-dimensional MR data reconstruction^1,2. However, TV often leads to patchy artifacts in the recovered images. We have proposed a generalized higher degree total variation (HDTV) scheme³ to reconstruct images from the noisy and undersampled measurements by taking into consideration of all rotations of the directional derivative operators, which overcomes the patchy artifacts caused by TV prior. In recent years, studies have shown that dynamic MRI reconstructions can be significantly improved by enforcing the low-rank constraint⁴. However, due to the high dimensionality of 4D MR data, the direct application of low-rank regularization is challenging. In order to address the problem, method that promotes local low-rank structure has been proposed⁵. However, the above mentioned methods are not able to fully exploit the spatio-temporal correlations of the 4D MRI data, thus have limited performance in accelerating 4D MRI. Here, we propose a new algorithm, which incorporates the three-dimensional 2nd degree HDTV component and the local low-rank component into a unified framework. We demonstrate that the proposed method is robust to motion and is able to reconstruct 4D MRI at high undersampling factors.

Methods

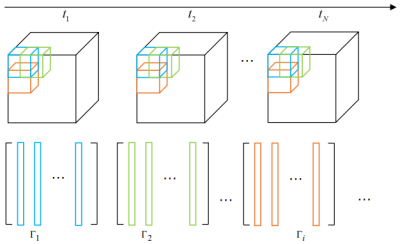
We rewrite the 4D MRI data in a Casorati matrix form $$$\mathbf X \in \mathbb C^{m\times T}$$$, where each column corresponds to the $$$m$$$ voxels in a time frame, and each row corresponds to the time profile of a voxel along $$$T$$$ time frames. The acquisition of the noisy and undersampled MRI measurements $$$\mathbf b$$$ can be modeled as $$$\mathbf b={\cal A}(\mathbf X)+\mathbf n$$$. Here, $$${\cal A}$$$ is the Fourier domain undersampling operator, $$$\mathbf n$$$ is the white Gaussian noise. Due to the high spatio-temporal correlation of the 4D data, the matrix $$$\mathbf X$$$ has the property of low-rank. However, due to the high dimensionality of the 4D MR data, direct application of the low-rank approach is challenging due to the anisotropy of the Casorati matrix, which could also lead to temporal blurring⁵. Thus, we propose to exploit the local low-rank property by decomposing the data into overlapping blocks in the spatial domain. Each block can thus be rearranged in a low-rank matrix. Fig.1 illustrates the formulation of the matrices based on the local low-rank structure. Moreover, higher degree total variation is demonstrated to considerably improve the image reconstruction performance over standard TV regularization, which enforces the sparsity of the higher order derivatives of high-dimensional data³. Thus, we propose to combine the three-dimensional 2nd order HDTV and the local low-rank penalties to recover the 4D MRI. The problem of recovering the MRI dataset $$$\mathbf X$$$ can be formulated as a constrained optimization function: $$\mathbf X^* =\min\limits_\mathbf X \|{\cal A}(\mathbf X)-\mathbf b \|^2+\lambda_1 \underbrace{\sum\limits_{t=1}^T\int_{\cal S}|\mathbf s^H(\mathbf u){\cal D}(\mathbf X^t)|d\mathbf u}_{\rm{HDTV}}+\lambda_2\underbrace{\sum\limits_{b=1}^K\|\mathbf P_b\mathbf X\|_*}_{\rm{Local\; low-rank}}$$ The optimization function includes the data consistency term, the HDTV, and the local low-rank terms. Here, $$$\mathbf X^t$$$ represents the data volume in the $$$t$$$-th time frame, i.e., the $$$t$$$-th column of $$$\mathbf X$$$. $$$\mathbf s^H(\mathbf u){\cal D}(\mathbf X^t)$$$ is the 2nd degree directional derivative of $$$\mathbf X^t$$$, $$${\cal D}(\mathbf X^t)$$$ is differential operator which provides the 2nd degree partial derivatives of $$$\mathbf X^t$$$, and $$$\mathbf s(\mathbf u)$$$ is the vector of polynomials in the components of the unit directions $$$\mathbf u \in {\cal S}$$$, where $$${\cal S}=SO(3)$$$ is the 3D rotation group, defined with the unit sphere. $$$\mathbf P_b$$$ is the binary matrix operator extracting the $$$b$$$-th block from the data, with the total number of blocks being $$$K$$$. $$$\|\cdot\|_*$$$ is the nuclear norm. $$$\lambda_1$$$ and $$$\lambda_2$$$ are balancing parameters. We use a variable splitting scheme followed by an alternating minimization approach to decouple the original optimization function into three subproblems, where two subproblems can be solved using shrinkage rules, and one quadratic subproblem can be solved with analytic solution. In addition, we adopt the continuation strategy in order to obtain a faster convergence.

Results and discussion

The proposed algorithm was applied on a real dynamic 4D cardiac MR dataset of the size 256×256×15×20, provided by the Department of Diagnostic Imaging of the Hospital for Sick Children in Toronto, Canada⁶. We used the 3D stack-of-stars golden angle radial k-space undersampling scheme⁷. The proposed HDTV-LLR scheme was compared with 4D-TV, iGRASP⁷, and the method using local low-rank penalty alone⁵. Fig.1 and Fig.2 show the recovery results from 12- and 16-fold undersampled measurements, respectively. We observe that the proposed method is able to recover images with sharper edges and lower errors.

Conclusion

We propose a HDTV-LLR method, which exploits the spatio-temporal correlation of the 4D MRI data by incorporating the three-dimensional HDTV and local low-rank constraints, in order to reconstruct 4D images at very high undersampling factors. We investigate the utility of the proposed method in recovering a 4D cardiac MRI data from 12-fold and 16-fold undersampled measurements. Results demonstrate the improved performance of HDTV-LLR over existing approaches.

Acknowledgements

No acknowledgement found.