3453
Versatile Parameter-Free Compressed Sensing MRI with Approximate Message Passing1Mathematical Institute, University of Oxford, Oxford, United Kingdom, 2Oxford Centre for Clinical Magnetic Resonance, University of Oxford, Oxford, United Kingdom, 3Siemens Healthineers, Princeton, NJ, United States
Synopsis
We consider two algorithmic challenges for the compressed sensing MRI community: (1) the difficulty of tuning free model parameters and (2) the need to converge quickly. The authors have developed a parameter-free approach to reconstruction which accommodates structurally rich regularizers that can be automatically adapted to near-optimality, removing the need for manual adjustment between images or sampling schemes. We evaluate the algorithm’s performance on three test images of varying type and dimension and find that it converges faster and to a lower mean-squared error than its competitors, even when they are optimally tuned.
Introduction
Compressed sensing MRI1 provides a toolbox of algorithms for reconstructing an image from undersampled k-space acquisitions. A challenge in compressed sensing frequently noted by researchers in the clinical community2,3 is the difficulty of tuning one or more model parameters $$$\lambda_i$$$, which is typically done by hand4. A greater number of $$$\lambda_i$$$s leads to a richer image model, however their optimal values are case-specific, depending on the undersampling scheme, sparsifying transform and image, and if tuned poorly can cause significant degradation in reconstruction quality. Previous methods5,6 have used Stein's Unbiased Risk Estimate (SURE)7 for automated regularization. However, these methods do not exhibit Gaussian effective noise so does not have a strong theoretical basis for implementing SURE and cannot guarantee near-optimal parameter selection.A second limiting factor for the clinical utility of compressed sensing MRI is the computational expense of reconstruction algorithms. For high-dimensional problems it may not be feasible to run an algorithm until convergence, which can limit the quality of reconstruction.
In response to these challenges, the authors recently developed the Variable Density Approximate Message Passing (VDAMP) algorithm for parameter-free compressed sensing MRI8. VDAMP exhibits a so-called "state evolution"9, where at every iteration the image estimate before thresholding behaves as the ground truth corrupted by Gaussian noise with zero mean and a covariance that is known and diagonal in the wavelet domain. To the authors' knowledge, VDAMP is the first reconstruction method for undersampled Fourier measurements of realistic images where a state evolution has been observed. A practical advantage of state evolution is that model parameters can be automatically tuned with SURE very effectively, so that near-optimal regularization can be achieved without the need for manual adjustment between image types or sampling schemes, and implies that a much richer image model can be accommodated, enabling higher order prior information such as anisotropy, variability across scales and structured sparsity. The automated regularization of VDAMP also addresses the problem of reconstruction time as the adaptive regularization is near-optimal on an iteration-by-iteration basis, so that each iteration is very effective and the algorithm converges rapidly. This work compares VDAMP to the Fast Iterative Shrinkage-Thresholding (FISTA) algorithm10 and an existing SURE-based parameter-free algorithm5 on three test images of varying type and dimension.
Method
Details of the algorithm can be found in the VDAMP paper8. All algorithms were implemented using the authors' VDAMP package available at https://github.com/charlesmillard/VDAMP. We considered three test images, which are shown in Fig. 1. Each image was retrospectively 2D undersampled in k-space at undersampling factor 5 using a mask generated with a polynomial probability density generated with the sparse MRI package available at https://people.eecs.berkeley.edu/~mlustig/Software.html. In all cases a Haar wavelet at 4 decomposition scales was used to sparsify the image. VDAMP was compared with FISTA in two cases: (1) with a sparse weighting $$$\lambda$$$ chosen to minimise the mean-squared error by an exhaustive search, referred to as Optimal FISTA; (2) a $$$\lambda$$$ that is fixed across image types, chosen to be the mean of the Optimal FISTA $$$\lambda$$$s, referred to as Shared FISTA. Further, as a baseline for a parameter-free algorithm, a version of FISTA that uses SURE to automatically tune threshold parameters5 was run, herein referred to as SURE-IT. For VDAMP and SURE-IT each wavelet subband had a separate iteration-dependant $$$\lambda_i$$$ tuned using a variation on the SureShrink denoiser11, as detailed in the VDAMP paper8. All algorithms were initialised with an image of zeros and run for 3 seconds.Results
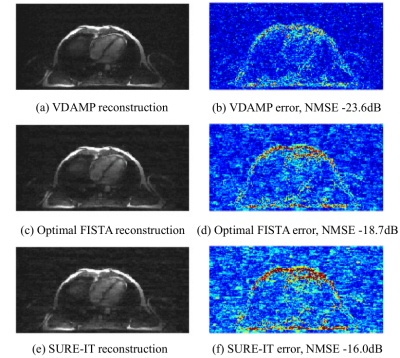
Fig. 2 shows the Normalised Mean-Squared Error (NMSE) of the algorithms verses compute time for each image type. Fig. 3 shows the VDAMP, Optimal FISTA and SURE-IT reconstruction of the cardiac image after 0.2s of compute time. Examples of the effective noise of SURE-IT and VDAMP are shown in Fig. 4, where the entry-wise absolute value of the difference between the estimate and the fully sampled image is shown in the wavelet domain for the first three iterations. Note that the VDAMP effective noise is Gaussian with zero mean and a covariance matrix that has one unique entry per wavelet subband, while no such behaviour is observed for SURE-IT. VDAMP has Gaussian effective noise in Fig. 4 only as its state evolution holds for the image estimate before thresholding; Fig. 3 shows the image post-thresholding, so there is visible bias in the noise.Discussion and Conclusions
These early-stage experiments indicate a number of practical strengths of VDAMP over algorithms currently used in the compressed sensing MRI literature. The richer sparse model made feasible by automatic regularization leads to a reduction in NMSE compared with FISTA, even when FISTA is optimally tuned. VDAMP's improvement in NMSE over SURE-IT highlights the need for Gaussian effective noise for proper parameter tuning with SURE. Future work includes VDAMP combined with parallel imaging and VDAMP with more sophisticated image models, such as multiple sparse domains. The rapidity of VDAMP's convergence indicates that the benefit of SURE outweighs the required additional computational expense, and could be clinically beneficial for high dimensional images or multidimensional data, where the per-iteration cost is high.Acknowledgements
This work was supported by an EPSRC Industrial CASE studentship with Siemens Healthineers, voucher number 17000051, and by The Alan Turing Institute under EPSRC grant EP/N510129/1. The concepts and information presented in this paper are based on research results that are not commercially available.References
1. M. Lustig, D. Donoho, and J. M. Pauly, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magnetic Resonance in Medicine, vol. 58, pp. 1182–1195, 12 2007.
2. A. Hsiao, M. Lustig, M. T. Alley, M. Murphy, F. P. Chan, R. J. Herfkens, and S. S. Vasanawala, “Rapid Pediatric Cardiac Assessment of Flow and Ventricular Volume With Compressed Sensing Parallel Imaging Volumetric Cine Phase-Contrast MRI,” American Journal of Roentgenology, vol. 198, pp. W250–W259, 3 2012.
3. K. G. Hollingsworth, D. M. Higgins, M. McCallum, L. Ward, A. Coombs, and V. Straub, “Investigating the quantitative fidelity of prospectively undersampled chemical shift imaging in muscular dystrophy with compressed sensing and parallel imaging reconstruction,” Magnetic Resonance in Medicine, vol. 72, pp. 1610–1619, 12 2014.
4. O. N. Jaspan, R. Fleysher, and M. L. Lipton, “Compressed sensing MRI: a review of the clinical literature,” The British Journal of Radiology, vol. 88, p. 20150487, 12 2015.
5. K. Khare, C. J. Hardy, K. F. King, P. A. Turski, and L. Marinelli, “Accelerated MR imaging using compressive sensing with no free parameters,” Magnetic Resonance in Medicine, vol. 68, pp. 1450–1457, 11 2012.
6. F. Ong, M. Uecker, U. Tariq, A. Hsiao, M. T. Alley, S. S. Vasanawala, and M. Lustig, “Robust 4D Flow Denoising Using Divergence-Free Wavelet Transform,” Magnetic resonance in medicine: official journal of the Society of Magnetic Resonance in Medicine/ Society of Magnetic Resonance in Medicine, vol. 73, p. 828, 2 2015.
7. C. M. Stein, “Estimation of the Mean of a Multivariate Normal Distribution,” The Annals of Statistics, vol. 9, pp. 1135–1151, 11 1981.
8. C. Millard, A. T. Hess, B. Mailhe, and J. Tanner, “An
Approximate Message Passing Algorithm for Rapid Parameter-Free Compressed
Sensing MRI,” 11 2019. [Online] https://arxiv.org/abs/1911.01234
9. D. L. Donoho, A. Maleki, and A. Montanari, “Message-passing algorithms for compressed sensing,” Proceedings of the National Academy of Sciences of the United States of America, vol. 106, pp. 18914–9, 11 2009.
10. A. Beck and M. Teboulle, “A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems,” SIAM Journal on Imaging Sciences, vol. 2, pp. 183–202, 1 2009.
11. D. L. Donoho and I. M. Johnstone, “Adapting to Unknown Smoothness via Wavelet Shrinkage,” Journal of the American Statistical Association, vol. 90, pp. 1200–1224, 121995.
Figures