Introduction

Compressed sensing (CS)1 MRI reconstruction exploits the sparsity of MR images, provides an important alternative to conventional parallel imaging reconstruction. It requires incoherent random undersampling, which leads to incoherent artifacts that can be iteratively eliminated by enforcing the transform sparsity. Multi-slice 2D Cartesian imaging is the most routinely used acquisition during clinical MRI scans, where undersampling can be only performed along phase-encoding direction. Such acquisition scheme inherently limits the image sparsity along the readout direction to be utilized in conventional single-slice CS. Multi-slice reconstruction via CS has been attempted earlier to explore the image sparsity (structural similarity) among slices1, where phase-encoding undersampling pattern was varied between slices but phase-encoding direction remained the same for all slices. However, this method only offered limited improvement because severe coherence still and only existed along phase-encoding direction. In this study, we propose a novel undersampling and reconstruction strategy. It significantly improves the incoherence of multi-slice Cartesian CS imaging by orthogonally alternating phase-encoding directions (APE) among adjacent slices. A new multi-slice CS approach is developed to exploit such enhanced sparsity along slice dimension. The proposed framework yield excellent CS reconstruction with undersampling flexibility, including both the conventional pesduo-random undersampling and the uniform undersampling (which is widely used in present parallel imaging method).

Method

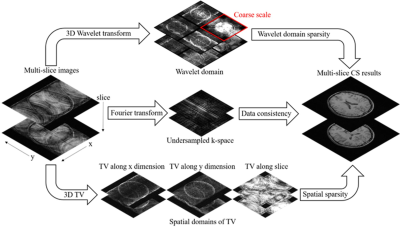
Multi-Slice CS Reconstruction
To take advantage of the sparsity across slices, conventional 2D CS1 is extended to multi-slice reconstruction by further applying 1D wavelet transform together with total-variation (TV) along the slice dimension, as shown in Figure 1. A lower regularization weight was implemented in 1D wavelet transform, since slice thickness/gap is typically larger than in-plane resolution. On the contrary, the additional TV is proposed to have a higher weight to enhance the leakage of artifacts among slices. In this study, the decomposition level of single-slice and multi-slice CS were set to 4×4 and 4×4×1 with Daubechies 4 wavelets.
Sampling Schemes
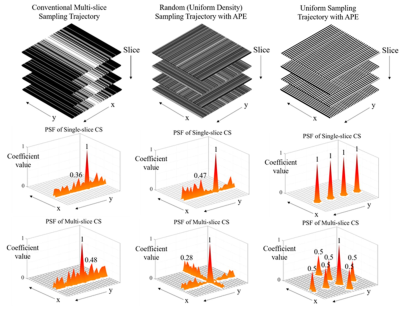
Conventionally, multi-slice 2D imaging with CS apply undersampling along the same direction for all slices (Figure 2). Though different slices can be undersampled differently, the incoherence among different slices is limited if all slices have the same aliasing direction. In our proposed approach, three different sampling patterns, including variable/uniform density random undersampling, and uniform sampling patterns, is augmented by APE. The point spread function (PSF)1 analysis was performed to evaluate sampling incoherence of these patterns.
Data Preparation and Image Reconstruction
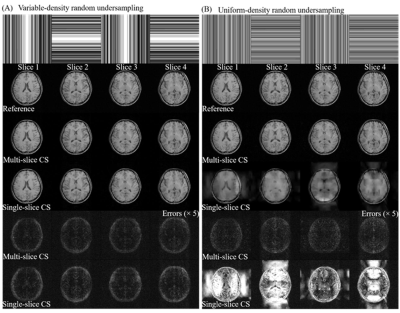
Human brain T1w and T2w data were acquired on a 3T Philips scanner with an 8-channel head coil. For T1w data, a gradient echo sequence (TR/TE=600/10ms, FOV=240×240mm², and slice thickness/gap=4/1mm) For T2w data, a fast spin echo (FSE) sequence (TR/TE=3000/113ms, FOV=240×240mm², and slice thickness/gap=4/1mm) and then retrospectively undersampled for evaluation. The multi-channel images were combined using virtual body coil method² to simulate single-channel data with phase information reserved, and then retrospectively undersampled using the aforementioned sampling with variable/uniform density random undersampling, and uniform sampling patterns. All the these pattern were augmented with APE. Multi-slice CS was performed on all 16 slices and 4 of them are shown.

Results

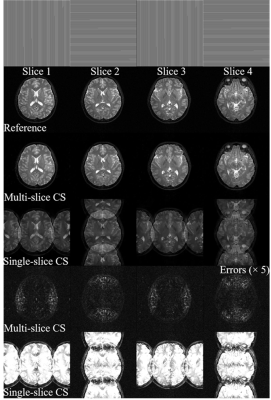
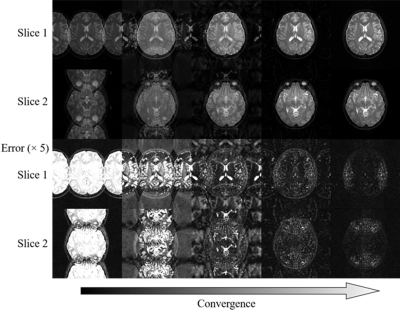
As shown in Figure 3, the multi-slice CS reconstructs better image structure and edges corresponding to the incoherency improvement examined by PSF in Figure 2. The image details in wavelet domain are corrupted by higher sidelobes of undersampling artifacts, thus become difficult to be recoverd in single-slice CS. For random undersampling without densely sampled k-space central region, multi-slice CS can still yield promising reconstruction because of the significant augmentation of coherence from APE sampling approach. Note that such augmentation even be effective when APE is applied with uniform undersampling pattern (Figure 4). Single-slice CS completely fails to remove extremely coherent artifacts, which is corresponding to the same level of coefficient compared to original signals in wavelet domain (Figure 2). With a simple APE sampling strategy, multi-slice CS is flexible to handle the uniformly undersampled single-channel data. Aliasing artifacts, that appeared only along undersampling direction, are spreaded into other slices and form pseudo-2D patterns through multi-slice CS (Figure 5).

Discussion and Conclusions

This study present a new acquisition and reconstruction strategy that can be easily applied to routine clinical multi-slice Cartesian CS imaging. The proposed alternating phase-encoding (APE) sampling greatly enhances the CS reconstruction by spreading artifacts among slices and in two directions, thus augementing the transform sparsity. Here we demonstrate that APE works with a variaty of sampling patterns, including variable/random and uniform undersampling. For simplicity, this strategy is implemented for single-channel multi-slice MR data only in this study. With multiple channels available in virtually all clinical MRI scanners, our proposed strategy can be easily incorporated into existing parallel imaging3 methods, and/or can be used to jointly reconstruct multi-channel MRI, by enforcing group sparsity for all channels to achieve very high acceleration. Furthermore, orthogonal APE as proposed in this study spreads aliasing along two orthogonal directions. However, this concept can be further extended by rotating the phase-encoding direction with different angles within spatially or/and temporally adjacent slices, which is conceptually similar to PROPELLER⁴ and GRASP⁵.

Acknowledgements

This study is supported in part by Hong Kong Research Grant Council (C7048-16G and HKU17115116 to E.X.W.), Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001) and Guangdong Key Technologies for Alzheimer's Disease Diagnosis and Treatment (2018B030336001) to E.X.W.