3447
Weighted-nuclear-norm minimization for low-rank approximation -- application to multi-shot diffusion-weighted MRI reconstruction1Department of Radiology, Stanford University, Stanford, CA, United States, 2Department of Electrical Engineering, Stanford University, Stanford, CA, United States, 3Department of Bioengineering, Stanford University, Stanford, CA, United States
Synopsis
Low rankness of image/k-space data has been exploited in many different MRI applications. In this work, we introduce weighted-nuclear-norm minimization for MRI low-rank reconstruction, in which smaller thresholds are used for larger eigenvalues to reduce information loss. Our simulation results demonstrate that weighted nuclear norm could serve as a better rank approximation compared to (unweighted) nuclear norm. With this technique, we achieve 10-shot DWI and high-fidelity half-millimetre DWI reconstruction with significantly reduced ghosting artifacts.
Introduction
Low-rank regularization has achieved success in a variety of MRI reconstruction tasks [1-7]. Figure 1 shows an example eigendecomposition of an 8-channel brain image along the channel dimension. Most signal lies in the space corresponding to the largest/first eigenvector, suggesting low rank along the channel dimension. While rank minimization is NP-hard, its convex envelope, the nuclear norm, is usually used to approximate the rank to reduce computational complexity [8].During the nuclear norm minimization process, eigenvalues of the low-rank matrix are soft-thresholded, usually using identical thresholds determined by the regularization parameter. Components corresponding to larger eigenvalues are more likely to represent the signal we want to preserve. A weighted-nuclear-norm minimization (WNNM) assigns different weightings and thus different thresholds, to different eigenvalues to reduce regularization of larger eigenvalues [9]. In this work, we apply WNNM to multi-shot diffusion-weighted imaging (DWI) reconstruction.
Theory
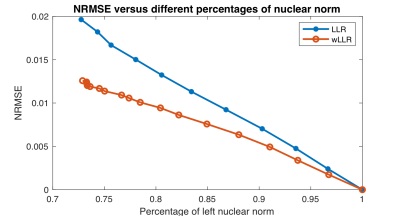
Weighted nuclear normThe weighted nuclear norm, or weighted summation of the eigenvalues of the matrix, can approximate the rank more accurately than the nuclear norm [10], and may therefore maintain the signal fidelity better while approaching low-rank approximation. To validate this, we use two different thresholding methods on the eigenvalues of matrices constructed from the 8-channel image as in [4] and calculate the normalized root mean squared error (NRMSE) between the compressed image and the original image. In the first method, locally low-rank (LLR), thresholds for all eigenvalues are the same, while in the second, weighted locally low-rank (wLLR), the threshold for the first eigenvalue is reduced 10-fold. Figure 2 demonstrates that, with the same nuclear norm after thresholding, wLLR better preserves the signal and achieves a lower NRMSE. Figure 3 shows compressed images (with about 73% nuclear norm left) using two methods, and LLR shows greater errors than wLLR. From the difference image, we can see that Fig. 3b (LLR) loses some structural details, while Fig. 3c (wLLR) still maintains high quality.
WNNM for multi-shot DWI reconstruction
Compared to single-shot DWI, multi-shot DWI enables higher resolution with reduced distortion artifacts, but suffers motion-induced shot-to-shot phase variations [11]. In shot-LLR [7], spatial-shot matrices are constructed and matrix completion is used to reconstruct the images, resolving phase variations. However, the number of shots is still limited. Similar to shot-LLR [4], we use a relaxed model and low-rank regularization term for multi-shot DWI reconstruction, but use a weighted nuclear norm term to approximate the rank regularization term as below,
$$$\min_{x} \sum_{s = 1 }^{NS}\frac{1}{2}\left \| E_{s}FS x_{s} - y_{s} \right \|_{2}^{2} + \lambda\sum_{l\in \Omega}\left \| R_{l}x \right \|_{w,*}$$$
where NS is the number of shots, E, F, and S are the sampling, Fourier transform, and sensitivity encoding operators, respectively, xs is the image of the s-th shot, and ys is the acquired k-space data of the s-th shot, |.|w, * represents the weighted nuclear norm operator, w represents the weightings for different eigenvalues, and $$$\lambda$$$ is the regularization parameter of the LLR term. Adaptive weightings based on eigenvalues and the regularization parameter are used to avoid the complexity of setting them [12, 13].
Methods
Data acquisitionUnder IRB approval, multi-shot EPI DWI data was acquired on six volunteers. Five volunteers’ brains were scanned on a 3T GE MR750 scanner using a 32-channel head receive-only coil with 4,6,8 and 10 shots, FOV (field-of-view)=20 cm, in-plane resolution=0.8 mm isotropic, slice thickness=4 mm, b-value=1000 s/mm2, and NEX (number of repetitions)=4.
To evaluate the effect of different in-plane resolutions, one brain volunteer was scanned on a 3T GE Signa Premier scanner using a 48-channel head receive-only coil with 6 shots, FOV (field-of-view)=20 cm, in-plane resolution=0.7,0.6 and 0.5 mm isotropic, slice thickness=4 mm, b-value=1000 s/mm2, and NEX=1.
Data preprocessing and reconstruction
The acquired data were processed using the product algorithm for Nyquist artifact correction and ramp sampling correction. Sensitivity map was calculated using BART [14] based on the non-diffusion-weighted data. All data were reconstructed by shot-LLR [7] and the proposed method, both using FISTA with 200 iterations, a regularization parameter of 0.008, and 8x8 patches for spatial-shot locally low-rank matrices [4]. The proximal operator of the weighted nuclear norm was to threshold the eigenvalues based on the corresponding weightings [9].
Results and discussion
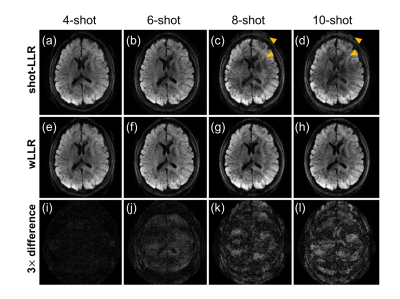
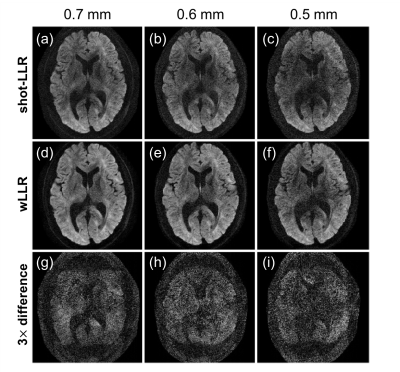
Figure 4 shows reconstructions for 4-10 shots. At 4 shots, shot-LLR and wLLR achieve similar results. As the number of shots increases, shot-LLR has signal loss (Fig. 4j), and increasing residual ghosting artifacts (Fig. 4c,d), compared with wLLR (Fig. 4e-h).Figure 5 shows that shot-LLR leads to signal loss especially in the center of the brain when compared with wLLR. The signal loss gets more prominent at higher in-plane resolutions. This suggests that wLLR retains useful information that would be lost if the same threshold was applied to different eigenvalues.
Different approaches to selecting and adapting the weights could be explored as WNNM is applied to a wide range of MRI low-rank reconstruction applications, such as spatio-temporal imaging [1-3], calibrationless parallel imaging [4,5] and multispectral imaging [6].
Conclusion
We demonstrated weighted-nuclear-norm minimization for MRI low-rank reconstruction. We showed that by using different thresholds for different eigenvalues, we could achieve 10-shot DWI and high-fidelity half-millimetre brain DWI reconstruction with reduced ghosting artifacts and information loss compared to unweighted nuclear-norm methods.Acknowledgements
R01-EB009055, P41-EB015891 and GE Healthcare.References
[1] Haldar JP, Liang ZP. Spatiotemporal imaging with partially separable functions: a matrix recovery approach. In: Proceedings of the 7th IEEE International Symposium on Biomedical Imaging: From Nano to Macro; 2010; Rotterdam, Netherlands; 716–719.
[2] Otazo, Ricardo, Emmanuel Candes, and Daniel K. Sodickson. "Low‐rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components." Magnetic Resonance in Medicine 73.3 (2015): 1125-1136.
[3] Zhang, Tao, et al. "Fast pediatric 3D free‐breathing abdominal dynamic contrast enhanced MRI with high spatiotemporal resolution." Journal of Magnetic Resonance Imaging 41.2 (2015): 460-473.
[4] Trzasko JD, Manduca A. Calibrationless parallel MRI using CLEAR. In: Proceedings of the Asilomar Conference on Signals, Systems, and Computers; 2011; Pacific Grove, CA; 75–79.
[5] Shin, Peter J., et al. "Calibrationless parallel imaging reconstruction based on structured low‐rank matrix completion." Magnetic resonance in medicine 72.4 (2014): 959-970.
[6] Levine, Evan, et al. "Accelerated three‐dimensional multispectral MRI with robust principal component analysis for separation of on‐and off‐resonance signals." Magnetic resonance in medicine 79.3 (2018): 1495-1505.
[7] Hu Y, Levine EG, Tian Q, et al. Motion‐robust reconstruction of multishot diffusion‐weighted images without phase estimation through locally low‐rank regularization. Magn Reson Med. 2019;81:1181–1190.
[8] Candes EJ, Recht B. Exact matrix completion via convex optimization. Found Comput Math. 2009;9:717–772.
[9] Gu, Shuhang, et al. "Weighted nuclear norm minimization with application to image denoising." Proceedings of the IEEE conference on computer vision and pattern recognition. 2014.
[10] Lu, Canyi, et al. "Nonconvex nonsmooth low rank minimization via iteratively reweighted nuclear norm." IEEE Transactions on Image Processing 25.2 (2015): 829-839.
[11] Wu W. Miller KL. Image formation in diffusion MRI: A review of recent technical developments. J Magn Reson Imaging. 2017;46:1–17.
[12] Candes, Emmanuel J., Michael B. Wakin, and Stephen P. Boyd. "Enhancing sparsity by reweighted ℓ 1 minimization." Journal of Fourier analysis and applications 14.5-6 (2008): 877-905.
[13] Gu, Shuhang, et al. "Weighted nuclear norm minimization and its applications to low level vision." International journal of computer vision 121.2 (2017): 183-208.
[14] Uecker M, Tamir J, Ong F, Holme C, Lustig M. Bart: Version 0.4.01; 2017.
Figures