3444

Phase Reconstruction using Iterative Multi-shot ESPIRiT (PRIME)

Stephen Cauley^1,2, Bryan Clifford³, Steffen Bollmann³, Thorsten Feiweier⁴, Berkin Bilgic^1,2, Kawin Setsompop^1,2,5, and Lawrence L. Wald^1,2,5
¹Department of Radiology, A. A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, ²Harvard Medical School, Boston, MA, United States, ³Siemens Medical Solutions USA, Boston, MA, United States, ⁴Siemens Healthcare GmbH, Erlangen, Germany, ⁵Harvard-MIT Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States

Synopsis

We employ a compact phase modeling strategy for accurate multi-shot echo-planar imaging (msEPI) reconstruction. As an alternative to approaches that perform msEPI reconstruction using strict low-rank constraints, we recast the problem as an iterative relative phase estimation problem. This allows for us to utilize existing techniques such as ESPIRiT, which are formulated for determining relative magnitude and phase differences between multi-coil receive arrays. Through an iterative search we jointly estimate an artifact-free combined image and the smooth relative phase between each msEPI shot. We demonstrate the benefits of our approach for clinical and highly-accelerated multi-shot diffusion-weighted acquisitions.

INTRODUCTION

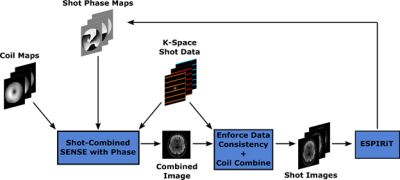
Single-shot two-dimensional (2D) echo-planar imaging acquisition methods are routinely used for both diffusion-weighted and functional magnetic resonance imaging (fMRI) studies. Several methods for acceleration have been explored to reduce the long pulse repetition time (TR) associated with high-resolution full-brain coverage imaging. Accelerated 2D parallel imaging (PI) techniques^1–5 are used to remove phase-encoding steps during an acquisition. These methods have many benefits, such as a reduction of image distortion and T2* blurring. These benefits are furthered through recent advances in model-based reconstruction, where joint reconstruction of multiple highly accelerated EPI shots is performed^6–8. In prior works^6,7, a low-rank representation for the block-Hankel matrix across shots was motivated. The foundation of these methods is an assumption that the smooth relative phase differences between the shots would live in the null space of the block-Hankel matrix, which is comprised of shifted copies of the k-space data. Although in certain scenarios these methods perform well, the underlying assumption need not be satisfied.

We build an iterative reconstruction framework (PRIME) that jointly estimates an artifact-free combined image and the relative phase between each msEPI shot. Throughout the PRIME algorithm we leverage ESPIRiT⁹ to arrive at smooth relative phases between the shots. The compact phase model provided by ESPIRiT relies on low-rank block-Hankel properties, locally low-rank properties, and spatial continuity of phase. Figure 1 shows an illustration of the method. Here, the initial phase of each shot is determined through individual-shot SENSE reconstructions. These shot-specific phases are then included in a SENSE reconstruction across all shots⁸. The combined image is then projected through the phase estimates and then coil sensitivities. The original k-space data is then integrated for data consistency. Coil combined shot images are fed through ESPIRiT to determine the relative phase differences and the process repeats until convergence.

METHODS

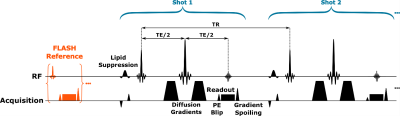
PRIME was performed using custom software written in MATLAB (Mathworks, MA, USA), and the data from a healthy volunteer were collected using a prototype sequence (Figure 2) on a 3T system (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany) in accordance with the local IRB. EPI diffusion data were acquired at 1.2×1.2×4.0mm³, R=1, 224×224mm² FOV, PF=6/8, 32 slices, b=1000 s/mm², and BW = 1132Hz/px using a 32-channel coil. Here, we considered fully sampled data arising from the use of 3 shots at [TR,TE] = [4800,94]ms, and 8 shots at [TR,TE] = [5400,51]ms.

RESULTS

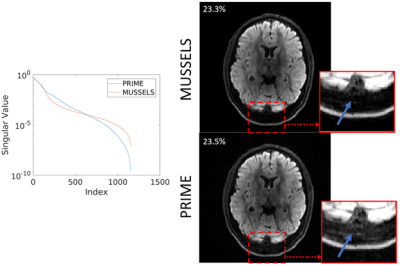
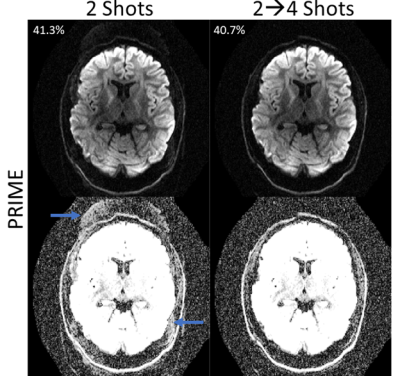
The accuracy of ESPIRiT for representing relative phase relationships in diffusion data was tested on 3 segment data. This R=3, b=1000 s/mm² data can be reliably reconstructed using SENSE and it is used as the ground truth. Figure 3 shows the magnitude and phase images from 2 of the single shot reconstructions. This complex data was used as input to ESPIRiT, with 48×48 calibration size and 12×12 kernel size, and the relative phase maps were extracted. The single shot SENSE and ESPIRiT phases were each used within combined-shot R=1.5 SENSE reconstructions, and the data consistency error was 39.4% and 40.6% respectively. Figure 4 shows a comparison of PRIME and MUSSELS⁶across 8 segments of fully-sampled data. To provide fair comparison between the methods, we use a consistent kernel size (12×12) and limit MUSSELS to a desired rank of “1” to match the “single” ESPIRiT maps. The singular value decay of the Hankel-matrix constructed from each reconstruction is shown on the left of Figure 4. The average magnitude image for MUSSELS and the combined-shot SENSE reconstruction for PRIME are shown with their respective data consistency errors. In the zoomed ROI we show the truncation of signal caused by the low-rank assumption of MUSSELS. Finally, Figure 5 shows the applicability of the PRIME algorithm for calibration-free removal of even/odd ghosts¹⁰. Here, the vendor ghost correction was disabled, and the acquired segments were separated into even and odd shots. Reconstruction improvement and data consistency error reduction are shown.

DISCUSSION AND CONCLUSION

We introduce an iterative approach for msEPI reconstruction based upon shot-combined SENSE and ESPIRiT phase estimation. We show the accuracy of the phase model using a standard clinical R=3 diffusion acquisition, see Figure 3. Here, the PRIME algorithm converges in a single iteration and the model accurately captures the significant phase variation to arrive within ~1% data consistency compared to the ground-truth. In contrast, the MUSSELS algorithm takes several steps (5-10) to impose the more stringent low-rank assumption.

In Figure 4, we have also shown the application of PRIME to highly-accelerated diffusion-weighted acquisitions. We achieve comparable data consistency error to MUSSELS with matched parameters and show better stability across the reconstructed shots (flatter singular value decay). In addition, the relaxed constraints afforded by the PRIME algorithm can also be clearly observed with the retention of signal near the skull. The ability of PRIME to model phase variation across even and odd EPI lines was shown in Figure 5. The data consistency error decreased, and the ghosts were substantially mitigated. Finally, this strategy aligns well with current ML guided msEPI reconstruction approaches as the shot-combined SENSE reconstruction can be integrated with ML priors.

Acknowledgements

This work was supported in part by NIH research grants: R01EB020613, U01HD087211, R01EB006847, R01EB019437, R24MH106096, P41EB015896, and the shared instrumentation grants: S10RR023401, S10RR019307, S10RR019254, S10RR023043

References

1. Griswold, M. A. et al. Generalized Autocalibrating Partially Parallel Acquisitions (GRAPPA). Magn. Reson. Med. 47, 1202–1210 (2002).

2. Pruessmann, K. P., Weiger, M., Scheidegger, M. B. & Boesiger, P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 42, 952–962 (1999).

3. Lustig, M., Donoho, D. & Pauly, J. M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58, 1182–1195 (2007).

4. Sodickson, D. K. & Manning, W. J. Simultaneous acquisition of spatial harmonics (SMASH): Fast imaging with radiofrequency coil arrays. Magn. Reson. Med. 38, 591–603 (1997).

5. Liang, D., Liu, B., Wang, J. & Ying, L. Accelerating SENSE using compressed sensing. Magn. Reson. Med. 62, 1574–1584 (2009).

6. Mani, M., Jacob, M., Kelley, D. & Magnotta, V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn. Reson. Med. (2017). doi:10.1002/mrm.26382

7. Haldar, J. P. Low-Rank Modeling of Local k-Space Neighborhoods (LORAKS) for Constrained MRI. IEEE Trans. Med. Imaging (2014). doi:10.1109/TMI.2013.2293974

8. Chen, N. kuei, Guidon, A., Chang, H. C. & Song, A. W. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage (2013). doi:10.1016/j.neuroimage.2013.01.038

9. Uecker, M. et al. ESPIRiT - An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 71, 990–1001 (2014).

10. Lobos, R. A., Javed, A., Nayak, K. S., Hoge, W. S. & Haldar, J. P. Robust autocalibrated loraks for EPI ghost correction. in Proceedings - International Symposium on Biomedical Imaging (2018). doi:10.1109/ISBI.2018.8363661

Figures

Figure 1: Illustration of the PRIME algorithm. Starting from initial phase estimates, the following steps are performed iteratively: (1) SENSE reconstruction across all shots using phase estimates; (2) apply shot phases and sensitivity maps to combined image; (3) merge with acquired k-space data for data consistency; (4) coil combine to form shot images; and (5) perform ESPIRiT to update estimate of shot phases.

Figure 2: Prototype multi-shot monopolar diffusion sequence used for PRIME data acquisition. Data for sensitivity map estimation were obtained from a low resolution, 2D FLASH reference scan acquired during the first 2.5s of the acquisition. Data for each shot were then obtained from successive, highly undersampled EPI readouts which were shifted in k-space such that the k_y-lines from each shot could be interleaved together to provide a single set of k-space data at the desired undersampling rate.

Figure 3: Demonstration of accuracy for ESPIRiT phase modeling applied to diffusion imaging at b=1000 s/mm². Phase estimation was performed across single-shot SENSE reconstructions for 2 of the 3 acquired shots. Shot-combined reconstruction was performed using the ground-truth and ESPIRiT maps. Data consistency error is shown in the top-left of the shot-combined magnitude images.

Figure 4: Comparison of PRIME and MUSSELS applied to diffusion imaging at b=1000 s/mm², across 8 highly-undersampled segments. The average magnitude image for MUSSELS and the shot-combined SENSE recon for PRIME are shown. The limited support constraint for MUSSELS can create sharp decreases in singular values (right) which results in signal dropout (highlighted boxes). The data consistency error for each method are shown in the top-left of the reconstructions.

Figure 5: Demonstration of EPI ghost correction using PRIME algorithm. Standard vendor phase correction for the data described in Fig. 3 was disabled. The standard phase model for the 2 shot data cannot capture the variation across the even and odd lines of each shot, leading to ghosts. The data is then separated into 4 shots and PRIME is applied to mitigate the ghosts. The data consistency error for each reconstruction is shown at the top left of each image.

Proc. Intl. Soc. Mag. Reson. Med. 28 (2020)

3444