3443
Robust Simultaneous Multi-Slice MRI Exploiting Hankel Subspace Learning with Self-Calibration and Self-Referencing Magnitude Prior1Sungkyunkwan University, Suwon, Republic of Korea, 2United Imaging Healthcare, Shanghai, China
Synopsis
SMS methods typically consist of the following two steps: kernel calibration and reconstruction. However, discrepancies between calibration and imaging occur due to either different image contrasts or subject motions, resulting in residual aliasing artifacts. To tackle these problems, in this work we propose a robust SMS technique exploiting Hankel subspace learning with self-calibration and self-referencing magnitude prior. An SMS filter is designed to strictly control pass-bands and stop-bands to reduce the dependence of image contrast on reconstruction. Both external and internal calibrating signals are included in the calibration step, while a self-referencing magnitude prior is imposed in the reconstruction step.
Introduction
Simultaneous multi-slice (SMS) MRI methods1-3, which encode several slices at the same time while resolving voxels in the slice direction using coil sensitivity information, has been a promising approach to speed up data acquisition, particularly for multi-slice 2D imaging. The SMS methods typically consist of the following two steps: kernel calibration and reconstruction. However, it should be noted that, discrepancies between calibration and imaging often occur due to either different image contrasts or subject motions, resulting in residual aliasing artifacts. To tackle these problems, in this work we propose a robust SMS technique exploiting Hankel subspace learning (SMS-HSL) with self-calibration and self-referencing magnitude prior. To reduce the dependence of image contrast on reconstruction, an SMS filter (equivalent to infinite impulse response (IIR) filter), employing the highly correlated Hankel-structured matrix, is designed to strictly control pass-bands (low rank prior) and stop-bands (null space projection)4. To alleviate motion induced discrepancies, both external and internal calibrating signals are included in the SMS calibration step, while a self-calibrating magnitude prior is imposed in the SMS reconstruction step. The effects of discrepancies between calibration and imaging are systematically investigated among split-slice GRAPPA(SP-SG)5, the proposed method, and generalized 3D GRAPPA6-8 for comparison.Materials and Methods
SMS Data Acquisition: Two sets of pelvis data were acquired in a volunteer on a 3T whole-body MR scanner (uMR770, UIH, Shanghai) using single band (SB) multi-shot FSE for retrospective SMS simulation studies and multi-band (MB) multi-shot FSE for prospective studies, respectively, in the presence of a certain level of subject motions. An additional set of SB data was acquired using conventional HASTE to emulate different image contrasts between calibration and imaging. In all studies, an MB factor and a CAIPI factor were all set to 3. The imaging parameters common in FSE were: TR/TE=4593/127.44ms(T2);2500/34.44ms(PD),flip angle=105°(T2);120°(PD),ETL=27(T2);6(PD),ESP=10.62ms(T2);11.48ms(PD),slice thickness=4mm(T2);3mm(PD),matrix size=304x548(T2);416x345(PD),the number of coils=20(T2);16(PD). Those specific to the prospective studies were: TR/TE=4500/128.96ms,flip angle=105°,ETL=27,ESP=9.92ms,slice thickness=4mm,matrix size=304x548x3,the number of coils=20. Those in conventional HASTE were: TR/TE=700/92ms,flip angle=150°. For the prospective studies, external calibration data were acquired using conventional HASTE, while self-calibrating data were acquired in line with imaging data by adjusting phase encoding blips.SMS-HSL with Self-Calibration and Self-Referencing Magnitude Prior: To reduce the dependence of image contrasts and subject motions on reconstruction, an SMS filter (equivalent to IIR filter) is designed using constrained optimization to strictly control pass-bands and stop-bands for aliasing separation with minimal inter-slice leakages. To this end, both external and internal calibrating signals are transformed to the highly correlated Hankel-structured matrix. The corresponding null space operator is then estimated in the HSL step4. The null space projection is to stop signals for removing undesired aliasing artifacts, while both the Hankel-structured low rank and self-referencing magnitude priors are to pass signals for preserving a slice of interest. Given the above considerations, aliasing separation in the proposed method is then formulated as the following unconstrained optimization problem by:
$$\hat{\textbf{x}}_\mathrm{s} = \mathrm{arg} \; \underset{\textbf{x}_\mathrm{s}}{\mathrm{min}} \; \frac{1}{2} \left \| \left ( \mathcal{H}\mathrm{\left ( \textbf{y} \right )}-\mathcal{H}\mathrm{\left ( \textbf{x}_\mathrm{s} \right )} \right ) \mathrm{\mathcal{N}^c_s} \right \|_{\mathrm{F}}^{2} + \mathrm{\lambda_L} \left \| \mathcal{H}\mathrm{\left ( \textbf{x}_\mathrm{s} \right )} \right \|_* + \mathrm{\lambda_M} \left \|\textbf{D} \textbf{x}_s - \textbf{r}_{sc} \right \|_{2}^{2} $$
where $$$ \mathcal{H}$$$ is the Hankel operator, $$$ \textbf{y}$$$ is the measured aliased SMS signals, $$$\textbf{x}_\mathrm{s}$$$ is the k-space data for the sth slice of interest, $$$\mathcal{N}^c_s$$$ is the null space operator for the sth slice, $$$\textbf{D}$$$ is the mask matrix indicating the self-calibrating region, $$$\textbf{r}_{sc}$$$ is the magnitude of the self-referencing calibrating signals for the sth slice, $$$ \left \| \cdot \right \|_*$$$ is the nuclear norm, and $$$\mathrm{\lambda_L}$$$ and $$$\mathrm{\lambda_L}$$$ are the regularization parameters. Thus, the first term plays a role of the null space projection, while both the second and third terms are to preserve signals in a slice of interest.
Results
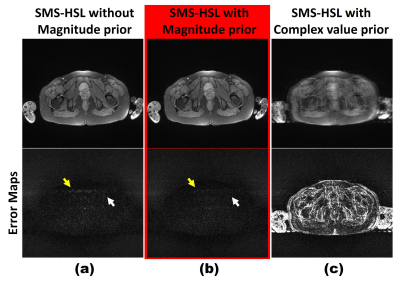
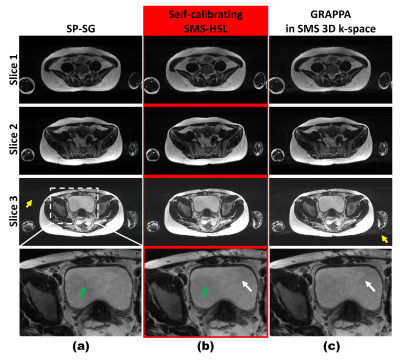
Fig.1-2 shows the effects of discrepancies between calibration and imaging due to different image contrasts(Fig.1) and subject motions(Fig.2). Fig.1 illustrates the dependence on the calibration data image contrast. Images in both the SP-SG and the 3D GRAPPA are contaminated by aliasing artifacts, while those in the proposed method are relatively clean. Fig.2 compares the proposed self-calibrating SMS-HSL with the SP-SG and the 3D GRAPPA by representing reconstructed images and the corresponding error maps using the simulated data. Despite of the presence of a certain level of subject motions, the proposed method exhibits robust suppression of artifacts and noise while the SP-SG and the 3D GRAPPA still suffers from remaining artifacts in the central region. Fig.3 shows the effectiveness of the magnitude priors in reducing artifacts and noise. Note that severe aliasing artifacts appears with a complex-value prior since there is substantial discrepancy in the phase of k-space between the calibration (either external or internal) and the corresponding SMS estimates due to subject motion. Fig.4 demonstrates the effectiveness of the proposed method in suppressing artifacts and noise using the prospective SMS data.Discussion and Conclusion
We successfully demonstrated the robustness of the proposed SMS-HSL with self-calibration and self-referencing magnitude prior in the presence of a certain level of subject motion compared to the split slice GRAPPA and the generalized 3D GRAPPA. It is expected that the proposed SMS method would widen its clinical applications, although it needs to be further investigated.Acknowledgements
This work is supported by NRF-2016M3C7A1913844, NRF-2017R1A2B4012581, 2018M3C7A1056887, and HI19C0149.References
1. Larkman DJ, Hajnal JV, Herlihy AH, Coutts GA, Young IR, Ehnholm G, et al. Use of multi coil arrays for separation of signal from multiple slices simultaneously excited. J Magn Reson Imaging. 2001;13:313-317.
2. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM, et al. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med. 2005;53:684-691.
3. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL, et al. Blipped controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med. 2012;67:1210-1224.
4. Suhyung P, Jaeseok P, et al. SMS-HSL: Simultaneous multislice aliasing separation exploiting hankel subspace learning. Magn Reson Med. 2017;78;1392–1404.
5. Cauley SF, Polimeni JR, Bhat H,Wald LL, Setsompop K, et al. Interslice leakage artifact reduction technique for simultaneous multi slice acquisitions. Magn Reson Med. 2014;72(1):93–102.
6. Zhu K, Kerr A, Pauly J, et al. Autocalibrating CAIPIRINHA: reformulating CAIPIRINHA as a 3D problem. In Proceedings of the 20th Annual Meeting of ISMRM, Melbourne, Australia, 2012. Abstract 518.
7. Zahneisen B, Poser BA, Ernst T, Stenger VA, et al. Three-dimensional Fourier encoding of simultaneously excited slices: generalized acquisition and reconstruction framework. Magn Reson Med. 2014;71:2071–2081.
8. Blaimer M, Breuer FA, Mueller M, Seiberlich N, Ebel D, Heidemann RM, Griswold MA, Jakob PM, et al. 2D-GRAPPA-operator for faster 3D parallel MRI. Magn Reson Med. 2006;56:1359–1364.
Figures
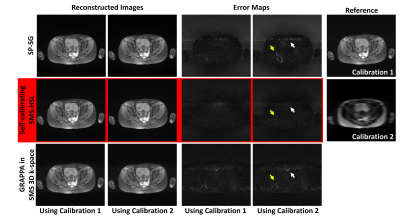
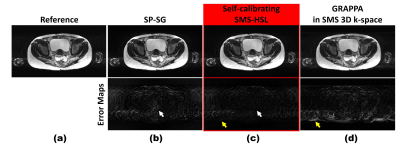
Figure 2. Images reconstructed using SP-SG (a), self-calibrating SMS-HSL (b), and generalized 3D GRAPPA (c) in the presence of a certain level of subject motion. Note that the proposed self-calibrating SMS-HSL produces high quality images while the SP-SG and the generalized 3D GRAPPA still exhibit aliasing artifacts resulting from discrepancy between calibration and imaging due to subject motions (white and yellow arrows).