Introduction

Magnetic Resonance Imaging (MRI) is a non-invasive imaging technique offering challenge of long scan time¹. Non-Cartesian trajectories help to reduce the scan time but require an extra step called gridding². In the recent past, GROG has been proposed to shift the non-Cartesian data points to the adjacent Cartesian positions via coil-by-coil weight sets². However, it leaves some unfilled spaces in the gridded data which leads to incoherent artifacts. Several algorithms have been proposed to overcome these artifacts^3,4,5; CS also being a good candidate. CS requires a small number of samples in the acquired k-space, incoherent artifacts and an appropriate non-linear reconstruction algorithm to efficiently reconstruct the artifact free MR image from the under-sampled k-space data⁶. This paper presents a new method ‘GROG with calibration-less pMRI for CS based p-thresholding’ to reconstruct the artifact free MR images from the radially encoded under-sampled k-space data.

Method

Gridding is a way to map the acquired non-Cartesian k-space data points onto Cartesian k-space². GROG transfers the non-Cartesian samples to the nearby Cartesian locations utilizing coil-by-coil self-calibrated weight sets leaving some unfilled positions in the gridded data^2,7.
Pseudo-Cartesian GRAPPA has been conventionally used for reconstructing the GROG gridded data to get the solution images using multiple coil-by-coil weight estimating patterns⁴. However, it is difficult to determine the correct choice and right number of the weight estimating patterns.
In the recent past, Projection onto Convex Set (POCS) algorithm was proposed in CS to recover the un-aliased MR images iteratively from the 2D variable density Cartesian under-sampled data³. p-thresholding is an extension of the iterative soft thresholding algorithm (ISTA) which has been used in literature to minimize the non-convex functions in CS⁹. The use of p-thresholding function promotes sparsity in the gridded k-space which is a key factor for CS based image reconstruction.
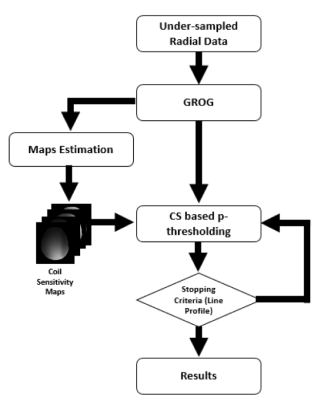
This paper proposes a new technique to reconstruct the fully sampled image from the highly under-sampled radial k-space data. Firstly, GROG transfers the acquired radial k-space points onto Cartesian k-space by using self-calibrated coil-by-coil weight sets. The receiver coil sensitivity maps are estimated from the center of the GROG gridded data using Eigenvalue maps estimation approach⁸. The receiver coil sensitivity profiles are incorporated with the CS based p-thresholding using adaptive coil combination method⁹ to recover the solution image. Figure-1 shows a block diagram of the proposed method. Mathematically, the optimization equation of the proposed method is:

min_s ||F_u.C.m - y_G||²₂ + λ||Xp(ψm)||₁ (Eq. 1)
where,
(X_p(ψm))_k = sign(ψm_k).max{0, |ψm|_k - λ|ψm|_k^p-1}

In eq.1, F_u is the under-sampled Fourier transform operator, C depicts the receiver coil sensitivity profiles, y_G is the GROG gridded data (y_G = G.Y_R; G is GROG operator and Y_R is the radially acquired k-space data), m is the reconstructed image, λ is the thresholding parameter, ψ is taken as a sparsifying transform (Wavelet) and Xp is the p-thresholding function.
In this work, the values of p (i.e. p = -0.05) and λ (i.e. λ = 0.3×10^-3) are empirically chosen after performing experiments for a range of values; and the correlation of the central line profiles of the reconstructed images between the current and previous iterations is used as a stopping criterion^2,10.

Results and Discussion

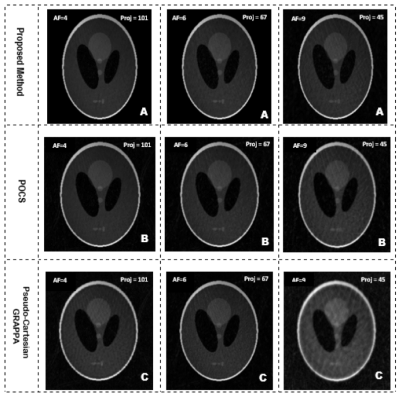
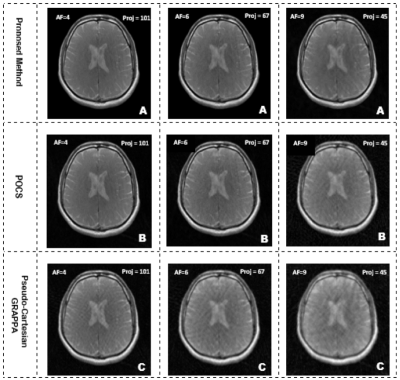
The proposed method is tested on the Shepp–Logan phantom and 1.5T human head data having dimensions 256×256×8. Initially, all the data sets are retrospectively encoded into radial projections using Fessler toolbox with the help of the following formula: (π/2)×FOV⁵.

Figure 2 and 3 show the reconstruction results of the proposed scheme (Row A), projection onto convex set (POCS) (Row B) and GROG followed by pseudo Cartesian GRAPPA (Row C) for Shepp–Logan phantom data and 1.5T human head data sets at AF 4, 6, and 9 with 101, 67 and 45 radial projections (Proj), respectively.

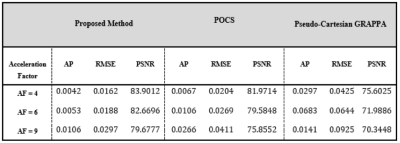
Table 1 and 2 show the AP, RMSE and PSNR values at AF =4, 6 and 9 of the Shepp–Logan phantom and 1.5T human head data reconstructed images .The proposed method gives better results both visually and in terms of quantifying parameters for Shepp–Logan phantom data (e.g. 77% and 86% improvement in AP, 5% and 32% improvement in RMSE , 7% and 11% improvement in PSNR at AF=4) and 1.5T human head data (e.g. 37% and 85% improvement in AP, 20% and 62% improvement in RMSE, 2% and 11% improvement in PSNR at AF=4) as compared to POCS and pseudo Cartesian GRAPPA, respectively.

Conclusion

In this paper, GROG with calibration-less pMRI for CS based p-thresholding is proposed to reconstruct the un-aliased MR images from the highly under-sampled radial k-space data. The proposed method efficiently eliminates the need of separate ACS lines and pseudo Cartesian GRAPPA patterns like conventional methods. The proposed work provides better results both visually and in terms quantifying parameters than POCS and pseudo Cartesian GRAPPA.

Acknowledgements

No acknowledgement found.