3440
Parallel MRI Reconstruction via Residual UNet with Joint Consideration of k-Space and Image Space
Xiaoxia Zhang1, Xiaopeng Zong1, Yong Chen1, Zhenghan Fang1, and Pew-Thian Yap1
1Department of Radiology, Department of Radiology and Biomedical Research Imaging Center (BRIC), University of North Carolina at Chapel Hill, Chapel Hill, NC, United States
1Department of Radiology, Department of Radiology and Biomedical Research Imaging Center (BRIC), University of North Carolina at Chapel Hill, Chapel Hill, NC, United States
Synopsis
We propose a strategy based on residual U-Net to reconstruct MR images from undersampled multichannel data by considering both k-space and image space. Our method first imputes the missing data points in k-space by utilizing the intrinsic relationships among channels. Then, the image reconstructed from the imputed k-space data is fed to another network for spatial detail refinement. Our method does not necessarily require auto-calibration signal (ACS) and is hence less susceptible to motion-induced inconsistency between the ACS and the undersampled data. Comprehensive evaluation indicates that our method yields images with superior perceptual details.
Introduction
MRI acquisition can be accelerated by undersampling k-space data in parallel imaging with a multichannel receiver coil. The raw data acquired from these channels can be combined using conventional methods, such as GRAPPA1 and SENSE2. In recent years, deep-learning-based reconstruction methods3-10 have shown improvements in reconstruction quality and achieved higher acceleration factor (R). However, existing methods usually require ACS. Most of them fail to consider the complementary information in k-space and image space and are limited to single-channel reconstruction with the magnitude images.In this work, we propose a reconstruction method based on residual U-Net (ResUNet)11 for multichannel MRI data involving both k-space and image space. We jointly consider the distinct data features in the different spaces, i.e. the data point correlation in k-space and the structural information in image space, and utilize the underlying relationships among channels with the complex-valued data. We conducted comprehensive comparisons with GRAPPA, ESPIRiT12, single-space network, single-channel network, and a recent deep learning method8.
Methods
Our work consists of two steps: (1) k-space imputation and (2) image refinement. A ResUnet is trained to impute the missing k-space data points for each channel. Then, another ResUnet is used to refine the image reconstructed from the imputed data.In the k-space, we utilize the underlying relationship among channels by employing assistance channels in reconstructing a target channel. Ideally, all channels should be used to reconstruct a target channel1. However, more channels will introduce more network parameters, potentially causing over-fitting and memory problems. As a compromise, we propose to use 1/3 of the channels to reconstruct a target channel by selecting assistance channels that give the top-ranking Pearson correlation coefficients with the target channel. Figure 1 depicts the architecture of the ResUNet with a long-skipped connection to speed up the training and force the network to focus on predicting the difference information. This network takes as input the undersampled k-space data from the target channel and its assistance channels. The outputs are the real and imaginal parts of the target channel. We minimize the L2 loss in k-space as in the GRAPPA formulation. The outer region of the k-space contains high-frequency contents and is more challenging to impute due to the low signal-to-noise ratio. To further reduce artifacts due to k-space imputation, k-space data are transformed to the image space using inverse Fourier transform and are fed into the image space network, which is also a ResUNet similar to the k-space network but without the long-skipped connection. Since the L2 loss function is known to cause image blurring13, we use the L1 loss to preserve image details.
Images were downloaded from the NYU fast MRI Initiative database8. They were acquired on the Skyra 3T scanner with a 2D TSE protocol using a 15-channel (N=15) knee coil. The matrix size is 320×320 with spatial resolution at 0.5×0.5×3 mm3. We randomly selected 167, 10, and 9 volumes for training, validation, and testing, respectively. The images were retrospectively undersampled with R at 2,4,6,8 with 7% as ACS and without ACS in a uniform scheme along the phase encoding direction.
Results
Quantitative image quality was evaluated using PSNR and Structural SIMilarity (SSMI). Table 1 gives the PSNR and SSIM results of different methods for different R values. Our method gives comparable PSNR and SSIM results when R is low (R = 2) with GRAPA and ESPIRiT. But when R is higher, the performances of the conventional methods dramatically deteriorate as expected while the proposed method is still able to reconstruct images with high quality. In comparison to the single-space networks, our method has superior results for all R values. Our method with channel assistance shows improvements for all ratios compared to the single-channel reconstruction. Examples of reconstructed images for R=6 are displayed in Figures 2 and 3. Figure 2 shows clear improvements with our method when compared to the conventional methods. In Figure 3, the zoomed-in regions show that more details are preserved and less artifacts are present using the proposed method. Table 2 gives the comparison when no ACS is included, and our method shows higher image quality.Conclusion
In this work, we present a dual-space reconstruction method for parallel MRI based on ResUNet. Our network takes full advantage of the intrinsic relationships among channels, and the distinct data features in k-space and image space. Our results demonstrate that the proposed method can achieve better image quality at acceleration factors R>4, compared with GRAPPA, single-space and single-channel networks. Improved image quality can be achieved for acceleration factors as high as 8 with ACS and 6 without ACS. Furthermore, both magnitude and phase images can be obtained with our method.Acknowledgements
This work was supported in part by NIH grant EB006733.References
- Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2002 ;47(6):1202-10.
- Pruessmann KP, Weiger M, Scheidegger MB, et al. SENSE: sensitivity encoding for fast MRI. Magnetic resonance in medicine. 1999 ;42(5):952-62.
- Hyun C, Kim H, Lee S, et al. Deep learning for undersampled mri reconstruction. Physics in Medicine & Biology,2018; 63(13), 135007.
- Schlemper J, Caballero J, Hajnal J, et al. A deep cascade of convolutional neural networks for mr image reconstruction. International Conference on Information Processing in Medical Imaging. Springer, 2017; 647–658.
- Quan T, Nguyen-Duc T, Jeong W. Compressed sensing mri reconstruction using a generative adversarial network with a cyclic loss,” IEEE transactions on medical imaging, 2018; 37(6), 1488– 1497.
- Eo T, Jun y, Kim T, et al. Kiki-net: cross- domain convolutional neural networks for reconstructing undersampled magnetic resonance images. Magnetic resonance in medicine, 2018; 80(5), 2188–2201.
- Zhang P, Wang F, Xu W, et al. Multi-channel generative adversarial network for parallel magnetic resonance image reconstruction in k-space. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, 2018; 180–188.
- Zbontar J, Knoll F, Sriram A, et al. fastmri: An open dataset and benchmarks for accelerated mri. arXiv preprint, 2018; arXiv:1811.08839.
- Xu W, Zhang Z, You Z, et al. Efficient deep convolutional neural networks accelerator without multiplication and retraining. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2018; 1100–1104.
- Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magnetic resonance in medicine. 2018;79(6):3055-71.
- Zhang Z, Liu Q, Wang Y. Road extraction by deep residual u-net. IEEE Geoscience and Remote Sensing Letters. 2018;15(5):749-53.
- Uecker M, Lai P, Murphy MJ, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic resonance in medicine. 2014;71(3):990-1001.
- Zhao H, Gallo O, Frosio I, Kautz J. Loss functions for image restoration with neural networks. IEEE Transactions on Computational Imaging. 2016;3(1):47-57.
Figures
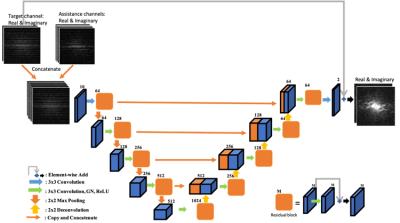
Figure 1. Illustration of k-space
network architecture for one target channel. The inputs are the real and
imaginary parts of the undersampled k-space data from the target channel and
its assistance channels. The outputs are the real and imaginary parts of the
k-space data for the target channel. The image space network shares the same
architecture, except the input and output are in image space.
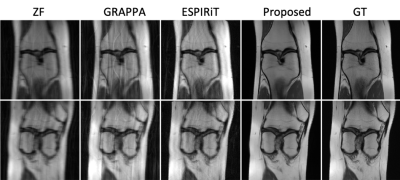
Figure 2. Examples of the
reconstructed images for R=6 with ACS using Zero-Filling (ZF), GRAPPA, ESPIRiT,
the proposed method, and the ground truth (GT).

Figure 3. Examples of the
reconstructed images for R=6 with ACS using k-space network, image space
(I-space) network8, single-channel network (SingleC), the proposed method,
and ground truth (GT).

Table 1. Averaged PSNR and SSIM of
the reconstructed images for different R values undersampled with ACS.
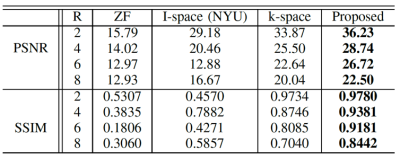
Table 2. Averaged PSNR and SSIM of
the reconstructed image for different R values undersampled without ACS.