Introduction

Modern MRI schemes rely on the spatial diversity of the coil sensitivities to recover the images from undersampled k-space measurements. Pre-calibrated¹, auto-calibrated, and calibrationless methods have been introduced for parallel MRI recovery. Pre-calibrated methods are prone to motion artifacts due to mismatches between calibration and main scans. Autocalibrating methods^2,3 overcome it by learning coil sensitivities from fully sampled center of k-space which often restricts the achievable acceleration. To minimize these trade-offs, researchers have introduced calibrationless parallel structured low-rank (PSLR) matrix completion approaches^4,5,6 that offer good performance at a high computational complexity.
We propose a deep learning strategy for calibrationless parallel MRI, which is computationally more efficient than PSLR algorithms. Similar to PSLR methods, the proposed scheme exploits annihilation relations in k-space except that they are pre-learned from exemplar data. We propose a model based approach⁷ and also additionally rely on a spatial domain deep learned prior to obtain a hybrid model that further improves reconstructions.

Proposed Method

The proposed deep learning architecture is motivated by the iterative reweighted least squares formulation of PSLR methods. It recovers multi-channel k-space data $$$\widehat{\boldsymbol \rho}$$$ from its Fourier measurements $$$\mathbf b$$$ by solving
\begin{equation} \arg \min_{\widehat{\boldsymbol \rho}} \|\mathcal{A}(\widehat{\boldsymbol \rho})-\mathbf b\|_2^2 + \lambda \|\mathcal T(\widehat{\boldsymbol \rho}) \|_\ast
\end{equation}
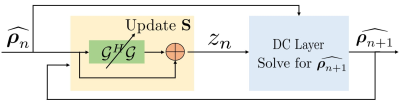
(see Fig. 2). By majorizing low rank prior and splitting variable as in O-MoDL⁹ we solve:
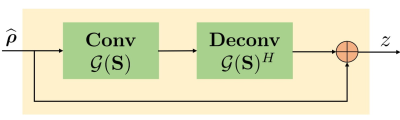
\begin{equation} \arg \min_{\widehat{\boldsymbol \rho}, \mathbf S, \mathbf z}\|\mathcal{A}(\widehat{\boldsymbol \rho})-\mathbf b\|_2^2 + \lambda \|\mathcal{G}(\mathbf S) \mathbf z\|_F^2+ \beta \| \widehat{\boldsymbol \rho} - \mathbf z\|_2^2 \end{equation} where $$$\mathcal A$$$ is an undersampling operator. Here, $$$\mathcal G(\mathbf S)$$$ is a block Toeplitz matrix representing convolution annihilation relations between coil images and sensitivities in Fourier domain. The IRLS solution iterates between null space $$$\mathcal G(\mathbf S)$$$ estimation, auxiliary variable $$$\mathbf z$$$ update and image $$$\widehat{\boldsymbol \rho}$$$ update (data consistency). The $$$\mathbf z$$$ update is interpreted as a denoising block (see Fig. 1) where it is projected orthogonally to null space $$$\mathcal G(\mathbf S)$$$:
\begin{equation}
\underbrace{\mathbf z_{n+1} \approx \left[\mathbf I ~-~\frac{\lambda}{\beta}~\mathcal G(\mathbf S_n)^H \mathcal G(\mathbf S_n) \right] \widehat{\boldsymbol \rho}_{n+1}}_{\textbf{$$$\mathcal L_n$$$, linear convolution-deconvolution denoiser block}} ...(1)
\end{equation}
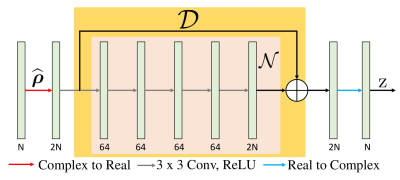
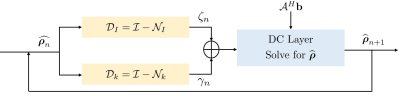
PSLR involves computationally expensive Toeplitz matrix lifting operation along with huge memory demand. We propose a fast model based deep learning approach. We replace the linear denoiser $$$\mathcal L_n$$$ with a non-linear CNN $$$\mathcal D_k$$$(see Fig. 3) where subscript $$$k$$$ means denoising in k-space,
\begin{equation}
\mathbf z_{n+1}= (\mathcal I - \mathcal N_k)\widehat{\boldsymbol \rho_n} = \mathcal D_k(\widehat{\boldsymbol \rho_n}) \hspace{4pt}....(2)
\end{equation}
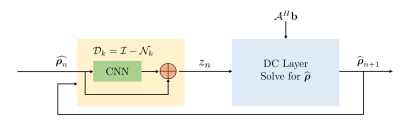
The algorithm alternates between the denoiser $$$\mathcal D_k$$$ and the analytical DC step:
\begin{equation}
\widehat{\boldsymbol \rho_{n+1}}= (\mathcal A^H \mathcal A + \beta \mathcal I)^{-1} (\mathcal A^H \mathbf b + \beta \mathbf z_{n+1}) \hspace{4pt}....(3)
\end{equation}
The proposed method called $$$\textbf{K-space}$$$ is summarized in Fig. 4. We learn the filter parameters of the unrolled network from exemplary data in an end-to-end fashion as in MoDL⁷. We exploit the multiple regularization prior incorporating ability of MoDL framework to add a spatial domain denoiser $$$\mathcal D_I$$$ in parallel to $$$\mathcal D_k$$$. This network is called $$$\textbf{Hybrid}$$$ (see Fig. 5).

Experiments and Results

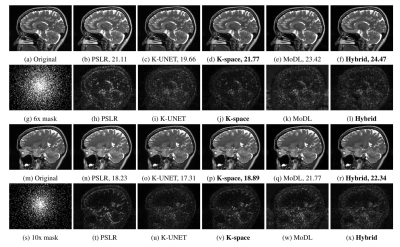
We conduct experiments on brain data collected from five subjects scanned at the University of Iowa Hospitals. A 3D T2 CUBE sequence was applied for Cartesian readout using a 12-channel head coil. Four subjects (90 x 4 = 360 slices) were used for training and the remaining one for testing. The experiments were conducted using a 2D non-uniform cartesian variable density undersampling mask with different acceleration factors; the readout direction was orthogonal to the slices.
We compare the proposed k-space alone (K-space) and hybrid (Hybrid) algorithms against PSLR, k-space UNET (K-UNET⁸) and MoDL. Brain reconstruction results with SNR are shown in Fig. 6. Note that MoDL is a calibrated deep learning approach, which additionally uses coil sensitivities to recover images in spatial domain; it uses more prior information, compared to all the other methods. K-UNET is a direct deep learning approach consisting of a 20 layer UNET without a DC step. The proposed K-space is the fastest with a reconstruction time of 0.05s compared to PSLR (367s), K-UNET(0.21s), MoDL(0.25s) and Hybrid(0.11s) respectively.
The K-space network performs better than both K-UNET and PSLR, but lags behind MoDL that uses additional coil sensitivity information and spatial regularization. We note that the Hybrid approach, which includes an image domain prior together with the k-space network improves the performance, thus outperforming the calibration-based MoDL scheme. The calibration-free strategy is desirable since it eliminates the vulnerability to potential mismatches between calibration and main scans.

Conclusion

We propose a calibrationless model based deep learning for Parallel MRI reconstruction. It is a non-linear extension of calibrationless PSLR methods that rely on annihilation relations in Fourier domain due to complementary information among coil images. The proposed method learns non-linear annihilation relations in the Fourier domain from exemplar data. The non-linearity helps to generalize learned annihilation relations over images unseen during training unlike structured low-rank methods which self learn linear annihilation relations from the input image every time. The proposed scheme is significantly faster than the SLR methods. We add an image domain prior to propose a hybrid network consisting of both k-space and spatial domain CNNs. The hybrid network out-performs the calibrated MoDL framework and other state-of-the-art calibrationless approaches.

Acknowledgements

This work is supported by NIH 1R01EB019961-01A1.