Introduction

Parallel imaging reconstruction for accelerated acquisitions is generally posed as an optimization problem, where a data consistency term is used to match the sampled points, and regularization terms may be added to impose prior knowledge about image characteristics ^1-5. One line of work is GRAPPA and its variants ^1-4, where convolutional kernels are used to interpolate missing k-space points. These kernels are calibrated to enforce linear dependencies in the fully sampled autocalibration signal (ACS). This ACS region can be reweighted to better emphasize high frequency regions ². Image phase can also be utilized to provide additional encoding via the virtual coil (VC) concept ^3,4. Another approach is to use neural networks for non-linear interpolation ^6-7. One such method is RAKI, where subject-specific CNNs trained on ACS data are used to interpolate missing k-space points ⁶. Limited degrees of freedom in receive arrays prevent parallel imaging from achieving high acceleration rates. Nonlinear interpolation fails to address this from limited ACS data as parameter estimation becomes ill-conditioned. We propose SPARK to lift these barriers by estimating reconstruction artifacts. SPARK assumes that these artifacts can be captured from the k-space errors in the ACS alone in a way that generalizes to the entire k-space, much like how dependencies captured from the ACS can be used to reconstruct missing points across the entire k-space. After these artifacts are estimated, they can be corrected for. Code/data: github.com/OBeker/SPARK.

Methods

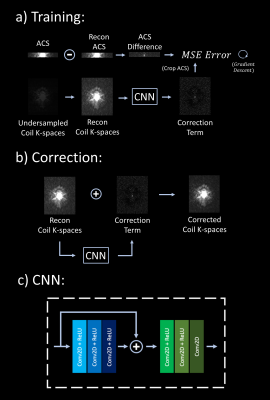
Training and artifact correction are depicted in Figure 1. After undersampled coil k-space is reconstructed with an existing method (e.g. GRAPPA, LORAKS), an individual CNN is trained to predict a correction term for the reconstructed k-space of that particular coil (i.e. 2n_c networks are trained in total). Each of these coil CNNs takes as input all of the reconstructed k-spaces across all coils, resulting in 2n_c input channels (n_c for real/imaginary parts). The network architecture was determined empirically. Each SPARK network S_c for coil c is trained with the following objective: $$\min_{\mathbf{w_{k}}}\ \left \|crop_{ACS}[S_c(\mathbf{w_{k}}; k)]-d_c \right \|_2$$ where w_c are the kernel weights, k are the reconstructed k-spaces across all coils. $$$d_c= ACS_c-crop_{ACS}[k_c]$$$ is the difference between the ACS lines of coil c and the corresponding lines in the reconstructed k-space for the same coil (where reconstruction is performed without substituting the ACS back). The predicted correction term is then added to the initial reconstruction.To demonstrate that SPARK can work synergistically with advanced reconstruction methods, we propose a refined GRAPPA employing Sparsity and VC concept (SVC-GRAPPA). This multiplies undersampled k-space data with diagonal matrices that implement horizontal and vertical gradient operators. VC-GRAPPA is then applied on the sparse gradient images, which are finally combined with a least squares formulation where data consistency is enforced ⁸. Exploiting sparsity allows SVC-GRAPPA to outperform GRAPPA especially at high acceleration.

Imaging Parameters:

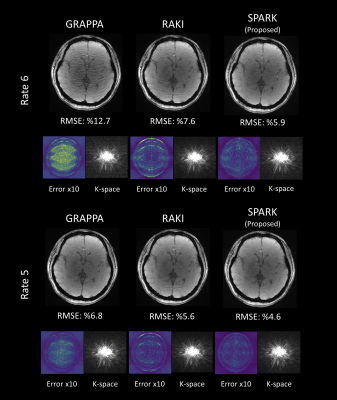
Figure 2: a volunteer was scanned with a 3T Siemens Prisma using a fully sampled GRE with FOV = 220x220mm², in-plane resolution = 0.7x0.7mm², matrix size = 320x320, slice thickness = 4mm, TR/TE = 500ms/14ms, flip angle = 70^o, 27 slices, bandwidth = 360Hz/pixel. Images were retrospectively undersampled to R = {4,5,6}. ACS size for all reconstructions is 40x320.
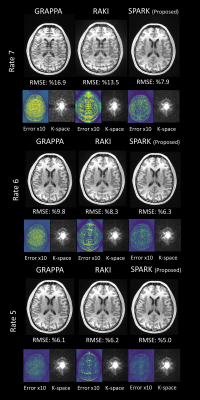
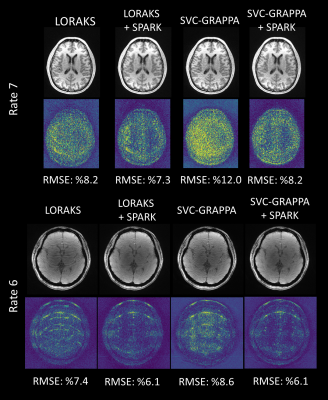
Figure 3: a volunteer was scanned with a Siemens 3T Skyra using a fully sampled MPRAGE at 1mm³ with FOV = 234x188x192mm³. Parameters were: TR=2530ms, TI=1100ms, TE=1.7ms, flip angle = 7^o, and bandwidth = 651Hz/pixel. Images were retrospectively undersampled to R = {5,6,7}. The ACS size used for all reconstructions is 30x188.

Both experiments used a 32-channel head-coil for reception. ACS data are substituted back in the conventional reconstructions.

Results

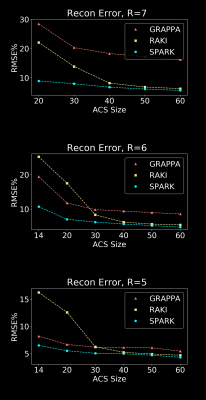
Figures 2 and 3 show the performance of SPARK applied on GRAPPA reconstructions. These results are compared with optimized (in terms of kernel size and Tikhonov regularization) GRAPPA and standard RAKI. In Figure 2, SPARK decreases RMSE by up to 2.1-fold compared with GRAPPA, and by up to 1.3-fold compared with RAKI. In Figure 3, SPARK reduces RMSE by up to 2.1-fold over GRAPPA; and by up to 1.7-fold over RAKI. SPARK’s ability to mitigate artifacts can be observed in the difference images and in k-space. Figure 4 compares SPARK, RAKI and GRAPPA for different ACS sizes and accelerations. SPARK is again applied to an initial GRAPPA reconstruction. Figure 5 shows the application of SPARK to advanced initial reconstructions, where up to 1.5- and 1.2-fold RMSE gains were observed over SVC-GRAPPA and LORAKS.

Discussion

We have proposed SPARK to combine sensitivity encoding and CNNs to enable high acceleration rates with improved quality. This network is trained in a scan-specific manner, only on the difference between ACS data and the corresponding region of a reconstructed k-space. This allows our method to work synergistically with well-established reconstruction methods without introducing artificial features. Beyond its ability to reduce RMSE and improve image quality at high acceleration, SPARK continues to provide benefits at moderate acceleration, where the initial reconstruction has minor artifacts. SPARK is also able to operate with stringent ACS sizes, where data-hungry nonlinear models fail to improve over GRAPPA. These properties suggest that SPARK is robust; with resulting images being at least as good as the initial reconstruction.

Acknowledgements

This work was supported by NIH research grants: R01EB020613, R01EB019437, R24MH106096, P41EB015896, shared instrumentation grants: S10RR023401, S10RR019307, S10RR019254, S10RR023043 and NVIDIA GPU grants.