3433
pISTA-SENSE-ResNet for Parallel MRI Reconstruction1Department of Electronic Science, Xiamen University, Xiamen, China, 2School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China
Synopsis
Magnetic resonance imaging has been widely applied in clinical diagnosis, however, is limited by its long data acquisition time. Although imaging can be accelerated by sparse sampling and parallel imaging, achieving promising reconstruction images with a fast reconstruction speed remains a challenge. In this work, we design the neural network structure from the perspective of sparse iterative reconstruction. The experimental results of a public knee dataset show that compared with the optimization-based method and the latest deep learning parallel imaging methods, the proposed network has less error in reconstruction and is more stable under different acceleration factors.
Purpose
Magnetic resonance imaging (MRI) plays an indispensable role in clinical diagnosis1. Parallel imaging2 and sparse sampling1 have been proposed to speed up the MRI signal acquiring process by reducing the acquisition of k-space data. However, the time-consuming iterations and the challenge to choose the optimal transform hinder its wide application. Recently, the data-based deep learning network3 has been applied in accelerating MR images reconstruction. In this work, inspired by unrolling iterative reconstructions as the structure of networks, we unroll pISTA-SENSE4-6 as network by replacing the hand-craft transform with CNN properly and use the residual structure to enhance the performance, expecting to get a lower reconstruction error than the existing method.Methods
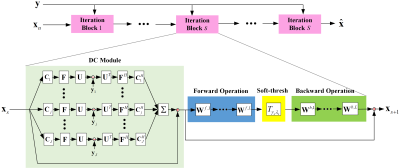
Our method, called pISTA-SENSE-ResNet, unrolled pISTA-SENSE 4-6 as the basic structure of our network. The pISTA-SENSE solves the reconstruction problem in SparseSENSE7 model, which applies sparse sampling to SENSE directly and written as: $$\underset{\mathbf{x}}{\mathop{\min }}\,\lambda {{\left\| \mathbf{\Psi x} \right\|}_{1}}+\frac{1}{2}\sum\limits_{j=1}^{J}{\left\| \mathbf{UF}{{\mathbf{C}}_{j}}\mathbf{x}-{{\mathbf{y}}_{j}} \right\|_{2}^{2}},(1)$$ where $$$\mathbf{x}$$$ is the desired composite MR image rearranged to a column vector, $$$\lambda $$$ is the regularization parameter, $$$\mathbf{\Psi }$$$ is the sparse transform which transposes the image into the space of sparse coefficients, $$${{\mathbf{C}}_{j}}$$$ is the sensitivity map of $$${{j}^{th}}$$$ coil, $$$\mathbf{F}$$$ is the Fourier transform, $$$\mathbf{U}$$$ is the undersampling matrix, $$${{\mathbf{y}}_{j}}$$$ is the acquired undersampled k-space data of the $$${{j}^{th}}$$$ coil.Each update step of iteration in pISTA-SENSE is replaced by different operations or modules of an iteration block in our proposed pISTA-SENSE-ResNet, shown in Fig.1. However, the iteration blocks in network is fixed in a small number $$$S=10$$$ compared with the pISTA-SENSE.
The DC module in the $$${{s}^{th}}$$$ iteration block of our pISTA-SENSE-ResNet keeps same with the one in pISTA-SENSE, which is built to keep the data consistency between the acquired k-space $$${{\mathbf{y}}_{j}}$$$data and the predicted one $$${{\mathbf{x}}_{s}}$$$ by the network and formulated as: $${{\mathbf{t}}_{s}}={{\mathbf{x}}_{s}}+{{\gamma }_{s}}\sum\limits_{j=1}^{J}{\mathbf{C}_{j}^{H}{{\mathbf{F}}^{H}}{{\mathbf{U}}^{T}}\left( {{\mathbf{y}}_{j}}-\mathbf{UF}{{\mathbf{C}}_{j}}{{\mathbf{x}}_{s}} \right)}, (2)$$ where $$$\gamma $$$ is the step size, the superscript $$$H$$$and $$$T$$$ denote conjugate transpose and transpose respectively. Another module consists of three operations and adds a skip connection, inspired by the ResNet8, to sum the input of first operation and the output of last operation to stabilize convergence, written as: $${{\mathbf{x}}_{s+1}}={{\mathbf{t}}_{s}}+{{Q}_{s}}\left( {{T}_{{{\lambda }_{s}}{{\gamma }_{s}}}}\left( {{P}_{s}}{{\mathbf{t}}_{s}} \right) \right) ,(3)$$ where forward transform and corresponding backward transform in pISTA-SENSE is replaced by 3-layers learnable CNNs, called forward operation$$${{P}_{s}}$$$ and backward operation $$${{Q}_{s}}$$$. The soft-thresholding operation $$${{T}_{\lambda \gamma }}$$$, which of threshold value $$${{\gamma }_{s}}{{\lambda }_{s}}$$$ varies in different iteration blocks, mimics the soft-threshloding function in pISTA-SENSE. Similar to9, the loss function in pISTA-SENSE-ResNet is specified by the sum mean square error between the fully sampled coil-combined image and the output of each iteration block.
Results
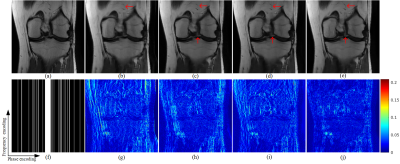
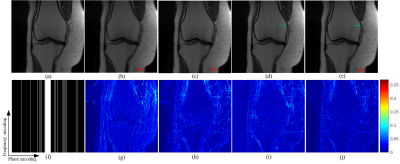
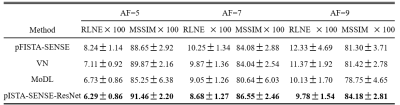
The public knee dataset provided by10 is used in our experiment. We choose 10 persons as the training dataset and another 5 persons for testing, and each person contains 20 slices of size 320$$$\times $$$320. Coil sensitivity maps are precomputed from a data block of size 24$$$\times $$$24 at the center of k-space using ESPIRiT11. Detailed, three 1D Cartesian random sampling patterns in phase encoding direction with acceleration factors of 5, 7, and 9 are adopted. To evaluate the performance of the proposed and compared methods, including data-free pFISTA-SENSE4,6 and data-based deep learning methods VN10 and MoDL12, relative $$${{l}_{2}}$$$ norm error (RLNE) and mean structure similarity index measure (MSSIM) 13 as the quantitative criteria.Among these reconstruction results, pISTA-SENSE-ResNet recovers the image more close to the fully sampled images: first, some details are recovered faithfully, while others not, such as the red arrow pointed in Fig.2 and Fig.3, second, the excessively sharp edge are well suppressed as the green arrows pointed in Fig.3. Besides this, less error is observed at the reconstruction results of pISTA-SENSE-ResNet according to the error maps. As shown in the TABLE I, pISTA-SENSE-ResNet reaches the lowest mean value of RLNE and highest mean MSSIM, which means our method reaches the least average reconstruction error and the superior detail recovery among these methods.
Conclusion
In this work, we proposed the pISTA-SENSE-ResNet to solve the parallel magnetic resonance imaging reconstruction problem, and the architecture of which is followed by unrolling the pISTA-SENSE. The long iteration step in the pISTA-SENSE is taken place by the cascade iteration blocks of the network, which favors the real-time reconstruction. Experiment results show, compared with the state-of-the-art deep learning methods under the public knee dataset, pISTA-SENSE-ResNet can recover images with more faithful details.Acknowledgements
This work was supported in part by National Key R&D Program of China (2017YFC0108703), National Natural Science Foundation of China (61571380, 61971361, 61871341, and 61811530021), Natural Science Foundation of Fujian Province of China (2018J06018), Fundamental Research Funds for the Central Universities (20720180056), Science and Technology Program of Xiamen (3502Z20183053), and China Scholarship Council. The authors would thank the GPU donated by NIVDIA Corporation.
The correspondence should be sent to Dr. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)
References
[1] M. Lustig, D. Donoho, and J. M. Pauly, "Sparse MRI: The application of compressed sensing for rapid MR imaging," Magnetic Resonance in Medicine, vol. 58, no. 6, pp. 1182-1195, 2007.
[2] J. Hamilton, D. Franson, and N. Seiberlich, "Recent advances in parallel imaging for MRI," Progress in Nuclear Magnetic Resonance Spectroscopy, vol. 101, pp. 71-95, 2017.
[3] S. Wang, Z. Su, L. Ying, X. Peng, S. Zhu, F. Liang, D. Feng and D. Liang, "Accelerating magnetic resonance imaging via deep learning," in IEEE International Symposium on Biomedical Imaging, 2016, pp. 514-517.
[4] Y. Liu, Z. Zhan, J. Cai, D. Guo, Z. Chen, and X. Qu, "Projected iterative soft-thresholding algorithm for tight frames in compressed sensing magnetic resonance imaging," IEEE Transactions on Medical Imaging, vol. 35, no. 9, pp. 2130-2140, 2016.
[5] S. Ting, R. Ahmad, N. Jin, J. Craft, J. S. d. Silveira, H. Xue, and O. P. Simonetti, "Fast implementation for compressive recovery of highly accelerated cardiac cine MRI using the balanced sparse model," Magnetic Resonance in Medicine, vol. 77, no. 4, pp. 1505-1515, 2017.
[6] X. Zhang, H.Lu, D. Guo, L. Bao, F. Huang, and X. Qu, "A convergence proof of projected fast iterative soft-thresholding algorithm for parallel magnetic resonance imaging," arXiv preprint arXiv:1909.07600, 2019.
[7] B. Liu, F. Sebert, Y. Zou, and L. Ying, "SparseSENSE: Randomly-sampled parallel imaging using compressed sensing," in Proceedings of the 16th Annual Meeting of ISMRM, 2008, p. 3154.
[8] K. He, X. Zhang, S. Ren, and J. Sun, "Deep residual learning for image recognition," in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770-778.
[9] X. Qu, Y. Huang, H. Lu, T. Qiu, D. Guo, V. Orekhov, and Z. Chen, "Accelerated nuclear magnetic resonance spectroscopy with deep learning," Angewandte Chemie International Edition, 2019. DOI:10.1002/anie.201908162.
[10] K. Hammernik, T. Klatzer, E. Kobler, M. P. Recht, D. K. Sodickson, T. Pock, and F. Knoll, "Learning a variational network for reconstruction of accelerated MRI data," Magnetic Resonance in Medicine, vol. 79, no. 6, pp. 3055-3071, 2017.
[11] M. Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S. Vasanawala, and M. Lustig, "ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA," Magnetic Resonance in Medicine, vol. 71, no. 3, pp. 990-1001, 2014.
[12] H. K. Aggarwal, M. P. Mani, and M. Jacob, "MoDL: Model based deep learning architecture for inverse problems," IEEE Transactions on Medical Imaging, vol. 38, no. 2, pp. 394-405, 2018.
[13] Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, "Image quality assessment: from error visibility to structural similarity," IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600-612, 2004.
Figures