Introduction

With conventional SENSE methods, some procedure is used to determine the sensitivity maps and those maps are used for image reconstruction [1]. These methods include SENSE, CS-SENSE [2], Sparse-SENSE[3], SPIRiT [4], ESPIRiT [5, 6], and SAKE+ESPIRiT [7]. Further gains in image reconstruction quality can be attained by permitting the sensitivity maps to vary along with the image and find a solution to both that best matches the data. JSENSE [8] and iSENSE [9] are examples of algorithms that take this approach. They alternate between two steps: 1) solve for sensitivity maps given the current reconstructed image, and 2) solve for the reconstructed image given the current estimates of the sensitivity maps. However, these algorithms are based on heuristic, polynomial-fit approaches that do not explicitly incorporate laws of physics.
In this work, we present a new technique that more fully takes advantage of prior information. Importantly, the algorithm is based on fundamental physics rather than heuristics. We call this technique the Iterative Multi-Coil Compressed Sensing Algorithm (iMCCS). A spatial bandwidth constraint is applied in accordance with the Biot-Savart law, and the nuclear-norm regularization is imposed in accordance with electromagnetic principles which require that the independence of the sensitivity maps is restricted to a few significant modes.

Methods

Let $$$s^{(c)}$$$ denote the $$$c^{\text{th}}$$$ coil sensitivity map for $$$C$$$ different coils. Let $$$s$$$ be the concatenation of all sensitivity map vectors into a single vector. The matrix $$$F$$$ is the discrete Fourier transform, and $$$\boldsymbol{F}=\text{diag}(F,F,\ldots,F)$$$. The matrix $$$M$$$ is a diagonal matrix where $$$M_{ii}\in\{0,1\}$$$ and indicates those data values that were measured, and $$$\boldsymbol{M}=\text{diag}(M,M,\ldots,M)$$$. The vector $$$b$$$ contains the sampled Fourier values. Let $$$S=[\text{diag}(s^{(1)}) \, \text{diag}(s^{(2)}) \, \cdots \, \text{diag}(s^{(C)})]^T$$$. Let $$$x$$$ denote the reconstructed image. The scalars $$$\lambda_x\geq 0$$$ and $$$\lambda_s\ge 0$$$ are regularization parameters provided by the user. They depend on the number of data points collected, the sampling pattern, and the dynamic range of the values collected by the machine.
We propose the following optimization problem where both $$$S$$$ and $$$x$$$ are optimization variables. It utilizes compressed sensing for image reconstruction and nuclear norm regularization for determining the sensitivity maps:
\begin{equation}
\begin{aligned}
\underset{S,x}{\text{minimize}} & \hspace{1em} (1/2) \left\|
\boldsymbol{M} \boldsymbol{F} S x - b \right\|_2^2 + \lambda_x \, \|W\,x\|_1 + \lambda_s \, \| \text{concat}(s) \|_\ast \\
\text{subject to} & \hspace{1em} D_{bw} \, F \, s^{(c)} = 0 \hspace{0.5em} \text{ for all } \hspace{0.5em} c\in\{1,2,\ldots,C\} \text{ and } \\
& \hspace{1em} |s_i| \leq 1 \hspace{0.5em} \text{ for all } \hspace{0.5em} i,
\end{aligned}
\end{equation}
where $$$\text{concat}$$$ is the isomorphism that concatenates the vectors $$$\{s^{(1)}, s^{(2)}, \ldots, s^{(C)}\}$$$ into the matrix $$$\boldsymbol{S}=[s^{(1)} s^{(2)} \cdots s^{(C)}]$$$, and $$$D_{bw}$$$ is a diagonal matrix such that $$$D_{bw,ii}\in\{0,1\}$$$ (the value is $$$0$$$ for any diagonal component corresponding to a spatial frequency less than $$$k_{bw}$$$ and $$$1$$$ otherwise). The sparsifying operator $$$W$$$ is the discrete Daubechies-4 Wavelet transform [10]. To solve the above problem, we employ the alternating minimization algorithm of Alg. 1.
To reconstruct the image given a set of sensitivity maps, one solves the following optimization problem. This is a convex optimization problem; it can be solved with FISTA.
\begin{equation}
\underset{x}{\text{minimize}} \hspace{1em} (1/2) \left\| \boldsymbol{M} \, \boldsymbol{F} S x - b \right\|_2^2 + \lambda_x \, \|W\,x\|_1, \label{eq:mccsProbDwork_findImage}
\end{equation}
To determine the sensitivity maps given the current estimate of the image, one solves the following optimization problem. This, again, is a convex optimization problem; it can be solved with the primal-dual hybrid gradient (PDHG) method [11,12].
\begin{equation}
\begin{aligned}
\underset{s}{\text{minimize}} & \hspace{1em} (1/2) \left\|
\boldsymbol{M} \, \boldsymbol{F} \boldsymbol{X} s - b \right\|_2^2 + \lambda_s \|\text{concat}(s)\|_\ast \\
\text{subject to} & \hspace{1em} D_{bw} \, F \, s^{(c)} = 0 \hspace{0.5em} \text{for all} \hspace{0.5em} c\in\{1,2,\ldots,C\} \text{ and } \\
& \hspace{1em} |s_i| \leq 1 \text{ for all } i,
\end{aligned}
\end{equation}

Results

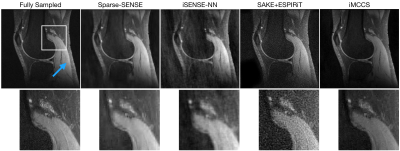
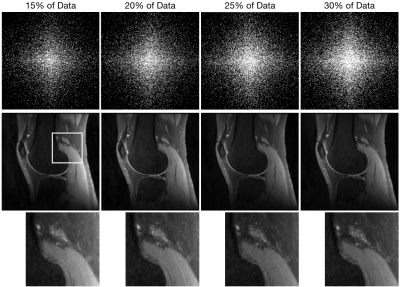
The reconstruction algorithm was applied to retrospectively undersampled knee MR images from mridata.org. The MR images were acquired with 8 channel coils at 3 T. The undersampling pattern was a variable-density separable Laplace distribution. In reconstruction, the Fourier data values were scaled so the largest magnitude was $$$1$$$, and regularization weights of $$$\lambda_x= 10^{-5}$$$ and $$$\lambda_s=10^{-2}$$$ were used. The value $$$K=50$$$. FISTA was run for $$$100$$$ iterations and PDHG was run for $$$300$$$ iterations. For comparison, a Sparse-SENSE reconstruction was also performed.

Figure 1 shows the comparison between Sparse-SENSE, iSENSE-NN, SAKE+ESPIRiT, and iMCCS with $$$20\%$$$ of the data. Figure 2 shows the quality of the iMCCS reconstruction as the percentage of data changes from $$$15\%$$$ to $$$30\%$$$. Even with a low data percentage of $$$15\%$$$ (compared to fully sampled data), the quality of the reconstruction is remarkably good.

Conclusion

In this work we presented iMCCS, a parallel-imaging and compressed sensing algorithm where the regularization functions imposed are based on Maxwell's equations. The iMCCS algorithm yields improved quality when compared with other algorithms. It is able to retain significant detail, even with a small fraction of the data required for full sampling. The results presented here did not include a calibration region, permitting increased acceleration factors over many standard techniques.
The computational cost of iMCCS is much higher than that of Sparse-SENSE or iSENSE-NN. In future work, we hope to reduce the time required for iMCCS by transferring significant portions of the computation to a Graphics Processing Unit.

Acknowledgements

No acknowledgement found.