Introduction

The geometry factor (g-factor) was originally proposed as a tool to help visualize the spatially-varying statistical uncertainty associated with accelerated data acquisition for SENSE¹. Subsequently, this concept was generalized for arbitrary linear image reconstruction techniques². Today, the g-factor is still widely used as a tool for comparing the advantages and disadvantages of different k-space sampling techniques and different image reconstruction techniques.

The conventional g-factor^1,2 is calculated voxelwise in the image domain and provides information about the noise amplification associated with each image voxel. The ability to quantify uncertainty in this way is desirable, since MRI benefits when there is as little uncertainty as possible. However, although it is natural to quantify uncertainty in the image domain, there are situations where it may be more natural to visualize uncertainty in a transform domain. For example, in sampling pattern design, it may be more useful to know which specific points in k-space are the most difficult to estimate (i.e., the most uncertain), so that these points can be specially targeted for data acquisition. As another example, there are some applications where faithful reconstruction of high-resolution image features and textures may be more or less important than faithful reconstruction of slow contrast variations. In such cases, a representation of uncertainty that provides information about these different spatial resolution scales could be quite valuable.

In this work, inspired by recent developments in uncertainty quantification and experiment design^3,4, we observe that it is straightforward to generalize the g-factor to arbitrary linear transform domains, including the Fourier domain (which provides an uncertainty measure for k-space) and the Wavelet domain (which provides an uncertainty measure for different resolution scales).

Theory and Methods

We consider a linear imaging model in which we make noisy k-space measurements $$$\mathbf{d}$$$ about an image $$$\mathbf{f}$$$ according to $$\mathbf{d} = \mathbf{E}\mathbf{f} + \mathbf{n},$$ where $$$\mathbf{E}$$$ is the forward encoding model and $$$\mathbf{n}$$$ represents noise. We assume that the noise $$$\mathbf{n}$$$ is zero-mean complex Gaussian with covariance $$$\boldsymbol{\Psi}$$$. Standard estimation theory results⁵ suggest that if $$$\mathbf{E}$$$ has full column rank, then the optimal minimum-variance unbiased estimate of $$$\mathbf{f}$$$ is unique and is given by $$\hat{\mathbf{f}} = (\mathbf{E}^H \boldsymbol{\Psi}^{-1} \mathbf{E})^{-1} \mathbf{E}^H\boldsymbol{\Psi}^{-1} \mathbf{d}.$$ Further,the covariance matrix of this estimate is equal to the Cramer-Rao bound⁵, and is simply given by $$$\mathrm{cov}(\hat{\mathbf{f}}) = (\mathbf{E}^H \boldsymbol{\Psi}^{-1} \mathbf{E})^{-1}.$$$ As such, the variance of the $$$m$$$th voxel $$$[\mathbf{f}]_m$$$ is given by the $$$m$$$th diagonal entry of the covariance matrix, i.e., $$$[(\mathbf{E}^H \boldsymbol{\Psi}^{-1} \mathbf{E})^{-1}]_{m,m}$$$. The conventional g-factor for the $$$m$$$th voxel in an accelerated scan is then obtained as the square-root of the ratio between the variance value obtained in this way and the variance value that would have been obtained from a fully-sampled acquisition, with additional normalization to account for the difference in acquisition time between the accelerated and fully-sampled scans¹.

The above approach enables calculating the image-domain g-factor, but in this work, we are interested in estimating transform-domain g-factors. Consider a transformation $$$\mathbf{T}$$$ that we can apply to the image $$$\mathbf{f}$$$ to get transform coefficients that we are interested in (e.g., Fourier-domain coefficients or Wavelet coefficients). A generalized statement of the Gauss-Markov theorem⁶ states that if $$$\hat{\mathbf{f}}$$$ is the optimal estimate of $$$\mathbf{f}$$$, then $$$\mathbf{T}\hat{\mathbf{f}}$$$ is the optimal estimate of its transform-domain coefficients, and the optimal covariance matrix for the transform coefficients is given by $$$\mathbf{T}(\mathbf{E}^H \boldsymbol{\Psi}^{-1} \mathbf{E})^{-1} \mathbf{T}^H.$$$ With this expression for the transform-domain covariance matrix, it is straightforward to derive a transform-domain g-factor with the same basic structure as the conventional g-factor, but using transform-domain variances instead of image-domain variances. Although the matrices involved in the calculation of this transform-domain g-factor are too large to store in memory, the results shown in this work are based on standard Monte Carlo methods that enable tractable computations².

Results

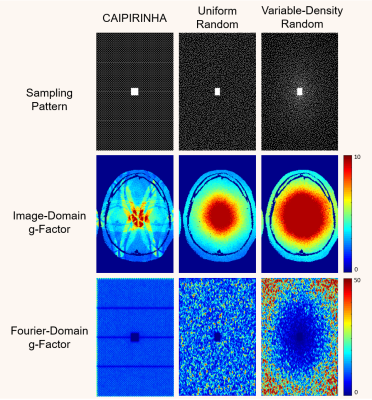
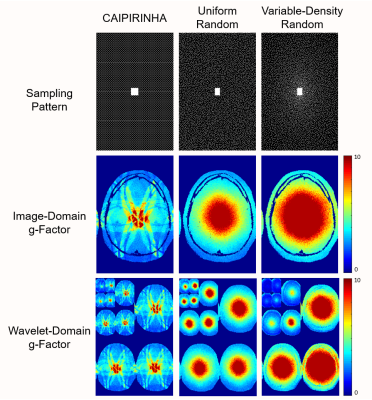
For illustration, Fig. 1 shows a comparison between image-domain g-factors and Fourier-domain g-factors for a 12-channel SENSE-based reconstruction with different sampling patterns. While the image-domain representation provides a useful quantification of voxelwise uncertainty, the Fourier-domain representation provides more direct insight into which specific regions in the Fourier domain are the hardest to estimate and may benefit the most from additional k-space measurements.

Fig. 2 shows a comparison between image-domain g-factors and Wavelet-domain g-factors for this same SENSE problem. Notably, the Wavelet-domain g-factor captures much of the same information as the image-domain g-factor, although provides additional information about uncertainty at different resolution scales. Notably, the top-left region in the wavelet domain corresponds to low-resolution image features, while the remaining regions correspond to progressively higher-resolution features, and e.g. we can clearly see that variable-density random sampling has less uncertainty for low-resolution image features and more uncertainty for high-resolution image features than the other two sampling patterns.

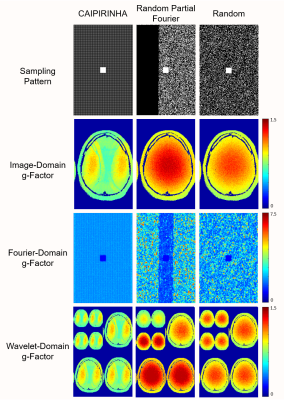
These ideas can also be applied naturally to other linear reconstruction formulations, as illustrated for phase-constrained SENSE⁷ in Fig. 3.

Conclusions

This work proposed transform-domain generalizations of the conventional image-domain g-factor. These generalizations provide additional insights that we expect to be useful for designing good k-space sampling trajectories. Although we’ve focused on linear reconstructions, there are potential ways to adapt this approach for nonlinear reconstruction (e.g., sparsity and low-rank) methods⁴.

Acknowledgements

This work was supported in part by research grants NSF CCF-1350563, NIH R01 MH116173, NIH R01 NS074980, and NIH R01 NS089212, as well as a USC Viterbi/Graduate School Fellowship.