3430
On Coil Combination with Optimal SNR for Linear Multichannel k-Space Reconstruction Methods1Electrical and Computer Engineering, University of Southern California, Los Angeles, CA, United States, 2Athinoula A. Martinos Center for Biomedical Imaging, Department of Radiology, Harvard Medical School, Massachusetts General Hospital, Charlestown, MA, United States
Synopsis
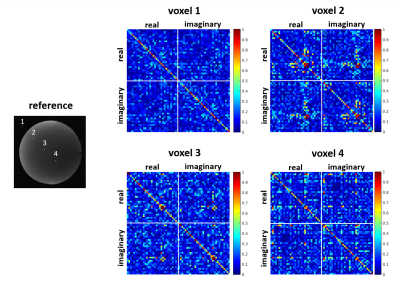
Noise correlations exist in multi-channel k-space data, and methods to optimally account for this correlation have been used for a long time in image-domain parallel imaging methods like SENSE. However, methods to address noise are not widely-utilized for Fourier-domain parallel imaging methods like GRAPPA, SPIRiT, and AC-LORAKS. In this work, we demonstrate that properly accounting for spatially-varying noise correlation can substantially reduce the noise level of coil-combined images. Further, we demonstrate the existence of previously-unknown correlations between the real and imaginary parts of the noise in reconstructed images. Accounting for this extra correlation can reduce the noise level even further.
Introduction
In multichannel MRI, the thermal noise samples from different receiver elements are often correlated with one another1. Methods that properly account for such noise correlation can be important to maximize image SNR. Techniques that address noise correlation are widely used by coil combination methods designed for fully-sampled data1 and accelerated image-domain parallel imaging methods like SENSE2,3. While there are also many popular linear Fourier-domain multichannel reconstruction methods (e.g., GRAPPA4, coil-by-coil SMASH5, SPIRiT6, PRUNO7, AC-LORAKS8, etc.), the post-reconstruction coil combination approaches that are used with these methods usually do not consider noise correlation. We are only aware of one previous attempt to address correlation issues for GRAPPA9, where it was demonstrated that accounting for the spatially-varying noise covariance of the reconstructed images could yield moderate improvements in SNR. In this work, we generalize this idea to the broader class of linear Fourier-domain reconstruction methods. In addition, we make the novel observation that the multichannel reconstructions obtained from linear Fourier-domain multichannel reconstruction methods often exhibit non-trivial crosscorrelations between the real and imaginary parts of the noise. Based on this observation, we propose an optimal improved approach that leads to even further improvements.Theory
Consider a scenario in which a vector $$$\mathbf{d}$$$ of undersampled noisy multichannel k-space data is measured. For simplicity, assume that this data has been pre-whitened3 so that it does not exhibit any noise correlations prior to applying a reconstruction procedure. Subsequently, a linear Fourier-domain reconstruction procedure (e.g., GRAPPA) is applied to this data to yield fully-sampled estimated k-space datasets for each channel, which are collected into the vector $$$\mathbf{k}$$$. Regardless of which reconstruction technique was used, linearity implies that we can write $$$\mathbf{k} = \mathbf{A}\mathbf{d}$$$ for some matrix $$$\mathbf{A}$$$. Finally, it is common to perform linear Fourier reconstruction of these estimated k-space datasets, which we denote by $$$\mathbf{f}=\mathbf{F}^{-1}\mathbf{k}$$$, where $$$\mathbf{f}$$$ is the vector of reconstructed multichannel images, and $$$\mathbf{F}^{-1}$$$ denotes the inverse Fourier transform operation. The final step in most image reconstruction pipelines is then to combine the images from multiple channels together. Even though we assumed that $$$\mathbf{d}$$$ was prewhitened, it is straightforward to show that the noise in the reconstructed multichannel images $$$\mathbf{f}$$$ is no longer white, and has a spatially-varying noise covariance matrix $$$\boldsymbol{\Psi}$$$ given by $$$\boldsymbol{\Psi}=\mathbf{F}^{-1}\mathbf{A}\mathbf{A}^H\mathbf{F}^{-H}$$$. While this covariance matrix is generally very large and intractable to work with, it is straightforward to estimate its components using existing Monte Carlo simulation methods10. To achieve optimal SNR, it is important to perform the final coil combination step while accounting for the spatially-varying covariance structure. When using a coil-combination approach that relies on sensitivity maps, then the standard "SNR-optimal” coil combination approach for a voxel $$$n$$$ with voxel-specific sensitivity map matrix $$$\mathbf{S}_n$$$ and voxel-specific noise covariance matrix $$$\boldsymbol{\Psi}_n$$$ is given by1-3 $$$(\mathbf{S}_n^H\boldsymbol{\Psi}_n^{-1}\mathbf{S}_n)^{-1} \mathbf{S}_n^H\boldsymbol{\Psi}_n^{-1}\mathbf{f}_n,$$$ where $$$\mathbf{f}_n$$$ is the vector of multichannel image data for the $$$n$$$th voxel. Importantly, the above procedure is only optimal if there is no correlation between the real and imaginary parts of the reconstructed image noise. However, in this work, we make the novel observation that there frequently does exist correlation between the real and imaginary parts of the noise for the Fourier-domain image reconstruction methods we consider. This correlation is illustrated in Fig. 1. To optimally account for this real-imaginary correlation structure, the previous coil-combination strategy should be replaced by $$\left[\begin{array}{cc}1\\i\end{array}\right]^T(\tilde{\mathbf{S}}_n^H\tilde{\boldsymbol{\Psi}}_n^{-1}\mathbf{S}_n)^{-1}\tilde{\mathbf{S}}_n^H \tilde{\boldsymbol{\Psi}}_n^{-1}\tilde{\mathbf{f}}_n,$$ where $$\tilde{\mathbf{S}}_n=\left[\begin{array}{cc}\mathrm{real}(\mathbf{S}_n)&-\mathrm{imag}(\mathbf{S}_n)\\\mathrm{imag}(\mathbf{S}_n)&\mathrm{real}(\mathbf{S}_n)\end{array}\right],$$ $$\tilde{\mathbf{f}}_n=\left[\begin{array}{c}\mathrm{real}(\mathbf{f}_n) \\\mathrm{imag}(\mathbf{f}_n) \end{array}\right],$$ and $$$\tilde{\boldsymbol{\Psi}}$$$ is the covariance matrix corresponding to separated real and imaginary components.Methods
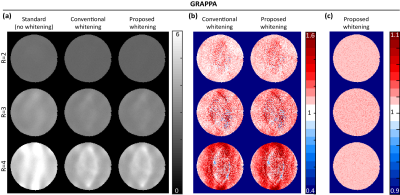
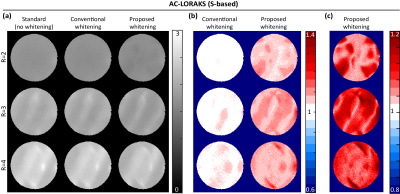
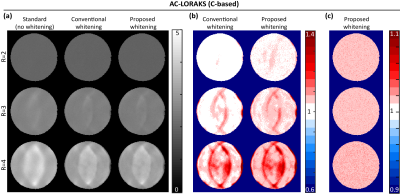
The proposed approach was investigated using real 32-channel phantom data. ACS data was obtained from a prescan, and sensitivity maps were also obtained using ESPIRiT11. Image reconstruction was performed using three different linear Fourier-domain methods (GRAPPA4, C-based AC-LORAKS8, and S-based AC-LORAKS8) for three different parallel imaging acceleration factors (R=2,3, and 4 with uniform undersampling). To assess SNR-optimality, theoretical noise standard deviation maps were obtained using Monte Carlo simulations10. We considered three different coil combination approaches: (1) the standard approach that ignores the spatially-varying noise correlations (i.e., assuming $$$\boldsymbol{\Psi}_n$$$ is the identity matrix for all voxels); (2) the "conventional whitening" approach9 that accounts for spatially-varying correlations but does not account for real-imaginary correlations; and (3) our proposed new whitening approach that accounts for both spatially-varying correlations and the correlations between the real and imaginary parts of the noise.Results
Results for the three different reconstruction methods are shown in Figs. 2-4. Results demonstrate that the improvements in the noise standard deviation can be substantial when using the conventional whitening procedure (~60% in some cases), and that our proposed new real-imaginary whitening procedure can lead to further additional improvements (~20% additional improvement beyond conventional whitening). However, the actual improvement levels that are achieved levels can vary substantially depending on the reconstruction method and the acceleration factor.Conclusion
Based on a novel observation about the structure of covariance matrices, we proposed and evaluated a novel method that can be used for optimal-SNR coil combination of the reconstructed multichannel images obtained from arbitrary linear Fourier-domain reconstruction methods. We observe that accounting for spatially-varying noise correlation can reduce noise substantially, while accounting for real-imaginary cross-correlations can reduce noise even further.Acknowledgements
This work was supported in part by research grants
NSF CCF-1350563, NIH R01-MH116173, NIH R01-NS074980, and NIH R01-NS089212.
References
1. Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magn Reson Med 1990; 16(2):192-225.
2. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999;42(5):952-62.
3. Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k‐space trajectories. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magn Reson Med 2001;46(4):638-51.
4. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47(6):1202-10.
5. McKenzie CA, Ohliger MA, Yeh EN, Price MD, Sodickson DK. Coil‐by‐coil image reconstruction with SMASH. Magn Reson Med 2001;46(3):619-23.
6. Lustig M, Pauly JM. SPIRiT: iterative self‐consistent parallel imaging reconstruction from arbitrary k‐space. Magn Reson Med 2010;64(2):457-71.
7. Zhang J, Liu C, Moseley ME. Parallel reconstruction using null operations. Magn Reson Med 2011;66(5):1241-53.
8. Haldar JP. Autocalibrated LORAKS for fast constrained MRI reconstruction. Proc IEEE ISBI 2015;910-13.
9. Polimeni JR, Setsompop K, Triantafyllou C, Wald LL. Optimal SNR combinations of multi-channel coil data for GRAPPA-reconstructed and time-series EPI data. Proc ISMRM 2013;3355.
10. Robson PM, Grant AK, Madhuranthakam AJ, Lattanzi R, Sodickson DK, McKenzie CA. Comprehensive quantification of signal‐to‐noise ratio and g‐factor for image‐based and k‐space‐based parallel imaging reconstructions. Magn Reson Med 2008;60(4):895-907.
11. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71(3):990-1001.
Figures