Introduction

In magnetic resonance thermometry based on the proton resonance frequency shift, the phase difference in an object before and after thermally induced changes is measured. With multi-coil measurements, coil data may be combined prior to or as part of the phase reconstruction algorithm. Trade-offs between computational expense and the temperature measurement precision of the phase reconstruction algorithm may determine how and when in the process multi-coil data is combined.

Phase Differencing With Multiple Coils
For two separate multi-coil measurements, the SNR-optimal phase difference resembles the general SNR optimal method for coil combination^1-4:
$$\label{eq:snr_optimal}\Delta \theta_j = \angle \bf{y}_{2j}\bf{R}^{-1}\bf{y}_{1j}^\dagger\tag{1}$$
where $$$\bf{R}$$$ is the noise covariance matrix, $$$\bf{y}_{nj}$$$ is the vector of coil measurements for voxel $$$j$$$ at time $$$n$$$, and $$$\dagger$$$ denotes the Hermitian transpose. In the context of thermometry, Equation \ref{eq:snr_optimal} may or may not be readily integrated into existing thermometry phase reconstruction algorithms.

A Hybrid Model of Thermally Induced Phase
Grissom et al. proposed a hybrid multi-baseline/referenceless phase reconstruction algorithm⁵ with the following (multi-coil) cost function over all $$$N_s$$$ voxels:
$$\label{eq:grissom_hybrid}\Psi(\bf{w},\bf{c}_{k=1}^{N_c},\bf{\theta}) = \frac{1}{2}\sum_{j=1}^{N_s}\sum_{k=1}^{N_c}\left|y_{kj} - \left(\sum_{b=1}^{N_b} x_{b,k,j}w_b\right)\exp\left[i({\bf{A}\bf{c}_k}_j + \theta_j)\right] \right|^2 + \lambda ||\bf{\theta}||_0\tag{2}$$
where $$$y_{kj}$$$ is the image at pixel $$$j$$$ for coil $$$k$$$, $$$\left\{\bf{x}_b\right\}_{b=1}^{N_b}$$$ are the complex baseline images, $$$\bf{A}$$$ is a matrix of low-order polynomial basis functions, $$$\bf{c}$$$ is a vector of polynomial coefficients, $$$\bf{\theta}$$$ is the thermally induced phase change, and $$$\lambda$$$ weights an $$$\ell_0$$$ regularization term. Grissom et al. iteratively minimized the cost with respect to $$$\bf{w}$$$, $$$\bf{c}$$$ or $$$\theta$$$ while holding the other parameters fixed. As opposed to Equation 1, in this approach, multi-coil data simply adds to the sum of errors in the objective function.

A Modified Multi-baseline Model
Let $$$\bf{R}^{-1}$$$ in Equation \ref{eq:snr_optimal} be decomposed as:
$$\bf{R}^{-1} = \bf{Q} \bf{\Lambda} \bf{Q}^{T}\tag{3}$$
We can compute decoupled data as:
$$\label{eq:data_decouple}\tilde{y}_j = \bf{\Lambda}^{\frac{1}{2}}\bf{Q}^T y_j\tag{4}$$
and our decoupled baselines as:
$$\label{eq:baseline_decouple}\tilde{x}_{bj} = \bf{\Lambda}^{\frac{1}{2}}\bf{Q}^T x_{bj}\tag{5}$$
We define a modified current measurement, $$$Y_j$$$ as follows:
$$\label{eq:y_new}Y_j = \bf{y}_j\bf{R}^{-1}\bf{y}_j^{\dagger} = \bf{\tilde{y}_j} \bf{\tilde{y}}_j^\dagger = \left|\tilde{y}_j\right|^2\tag{6}$$
and modified baselines, $$$X_{bj}$$$ as follows:
$$\label{eq:x_new}X_{bj} = \bf{y}_j^\dagger\bf{R}^{-1}\bf{x}_{bj} = \bf{\tilde{y}_j}^\dagger\bf{\tilde{x}}_{bj}\tag{7}$$
These terms (Eqs.\ref{eq:y_new} and \ref{eq:x_new}) are then substituted for $$$y$$$ and $$$x_b$$$ in multi-baseline portion of Equation \ref{eq:grissom_hybrid}.

Methods

One healthy volunteer was imaged on a 3T scanner (MAGNETOM Prisma^Fit, Siemens Healthcare, Erlangen, Germany) using a prototype 3D segmented EPI sequence with following parameters: TR 45ms, TE 24ms, 1.25x2.5x2.5mm³ resolution, 192x96x12 matrix (10 partitions with 20% oversampling), 80 repetitions, FA 15, BW 1240, ETL 9, 5.94~s/image, w/Fat sat. No thermal therapy was performed.

A 2D navigator was employed to detect phase drift in the system. All coil data was decoupled as in Equations \ref{eq:data_decouple} and \ref{eq:baseline_decouple}. The first 20 of 80 repetitions were selected as baselines and used to construct 3D phase images of the other 60 repetitions using a modified form of Grissom et al.'s algorithm.

Three coil-combination methods were considered: two that combined coil data prior to invoking the phase extraction algorithm, and one that fed multi-coil data directly to the phase extraction algorithm. The two pre-combining methods combined coil data using either Adaptive Combine^6,7 or a Roemer-like combine (Equations \ref{eq:y_new} and\ref{eq:x_new}). The final method employed the original multi-coil phase reconstruction algorithm (Equation \ref{eq:grissom_hybrid}) without the referenceless and $$$\ell_0$$$ regularization terms.

Reconstructions were performed by feeding data to the phase extraction algorithm on a slice-by-slice basis (2D) or full volume (3D) basis. The navigator acquired estimate of the phase drift was modeled with a linear function and removed from the final 60 phase volumes prior to computing temperature measurement precision. Reconstruction times (mean time per repetition) and temperature measurement precision across the 60 repetitions were used as performance measures.

Results

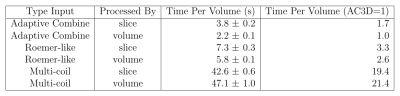
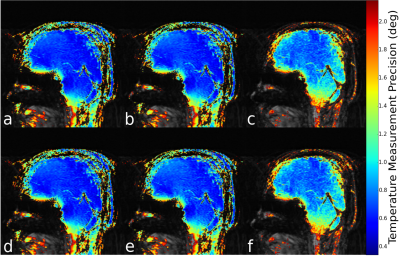
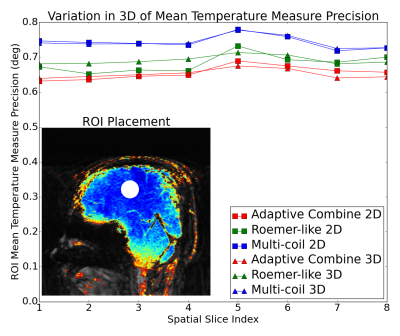
Table 1 shows execution times per 3D reconstruction for each of the coil combination methods considered.
Figure 1 shows the temperature measurement precision across 60 measurements for the middle slice for the different coil-combination methods considered. Lower values are better. Figure 2 shows the mean temperature measurement precision within the indicated ROI across the 3D volume.

Discussion

Execution time scaled with the number of coils input to the phase reconstruction algorithm. Performing coil combination within the phase reconstruction algorithm is less stable, resulting in poorer temperature measurement precision. Applying the phase reconstruction algorithm to the full 3D volume is preferable to treating each slice individually, especially toward the edge slices where the signal is lower.

Conclusion

Computational times are significantly reduced by combining coil data prior to invoking the phase reconstruction algorithm. While this means that the noise in the combined coil measurements no longer matches the assumed Gaussian distribution of the phase reconstruction algorithm's penalized-likelihood solution, multi-baseline convergence does not appear to be significantly affected and the computed phase is comparable to the multi-coil approach.

Acknowledgements

This project was supported by Siemens Medical Solutions, a University of Utah seed grant, the Mark H. Huntsman endowed chair and NIH grants R03EB023712, R37CA224141, and S10OD018482