3426
EPI Phase correction using model-based deep learning reconstruction1Institute of Science and Technology for Brain-Inspired Intelligence, Fudan University, Shanghai, China, 2MR Collaboration, Siemens Healthcare Ltd., Shanghai, China, 3Human Phenome Institute, Fudan University, Shanghai, China
Synopsis
The commonly used approach of Nyquist ghost correction in echo planar imaging (EPI) include linear phase correction and model-free 2D phase correction. The recent proposed method termed ‘PEC-SENSE’ incorporates 2D phase error correction with parallel imaging can robustly eliminate Nyquist ghost for EPI data,while does not act well when a distortion mismatch exsisted between the calibration data and image data. The proposed model-based deep learning method can obtain more robust phase maps than PEC-SENSE to remove image ghost and preserve the image SNR in low or high-accelerated EPI data.
Introduction
Diffution weighted imaging(DWI), Diffution tensor imaging(DTI), Functional MRI(fMRI) with same EPI readout gradient waveform play a critical role in clinical and research applications. One of the most common artifacts in EPI is Nyquist ghost, which is induced by phase inconsistency between opposite readout polarities. Linear phase correction can not eliminate the high order phase errors induced by the varying eddy current or unbalanced time delay in gradient system. Consequently, an EPI 2D phase correction method PEC-SENSE was proposed1,2, which estimated the 2D phase error map of the positive and negative echoes images was unaliased by SENSE. However the error and noise in the phase error map can affect Nyquist ghost removal and the final image SNR, especially for highly accelerated data. In this study, phase error map can be obtained by using a model-based deep learning network, which enforce data-consistency by using numerical optimization blocks within the network3.The proposed ‘Deep-PEC’ based phase error map will replace the original phase error map calculated from SENSE.Methods
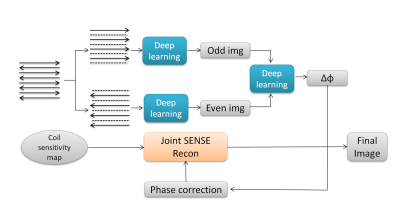
The existing 2D phase correction method calculated the phase error map from two ghost-free images aliased by SENSE and incorporate it into the joint SENSE reconstruction of both positive and negative echoes to obtain the final ghost-free images. In this study, this phase error map was replaced by one obtained from a model-based deep learning network. The procedure of reconstruction is showed in Fig1.Network Architecture
The CNN Architecture includes a pre-trained CNN denoiser and data-consistency by using conjugate gradient algorithm within the network. The CNN has 5 layers totally with 64 filters, and each layer is composed of a convolution followed by a batch normalization and a non-linear activation function ReLU3,4,5. The number of iterations is selected to 50. The network was implemented with Tensorflow library in Python 3.6 and trained with NVIDIA DGX GPU.
Data Acquisition
The images were acquired from five volunteers on MAGNETOM Prisma 3T of Siemens. Single-shot DWI was obtained using a 64-channel head coil. Each data includes 19 slices, resulting in a total of 95 images. Data were acquired with sense and without sense for validation.Data parameters: FovRO = 220, FOVPE = 220, MatrixRO = 192, MatrixPE = 192, TR = 4900, TE = 100(appropriation factor = 2) and 164(full sampling).
Training dataset
The four full sampled ghost-free data and corresponding mask were used to simulate the SENSE calculation at various acceleration factors to acquire appropriate network parameters. The other one data was used to test the performance of the CNN at different acceleration factors.
Quantitative analysis
PSNR was calculated to evaluate the performance of phase correction.
Results
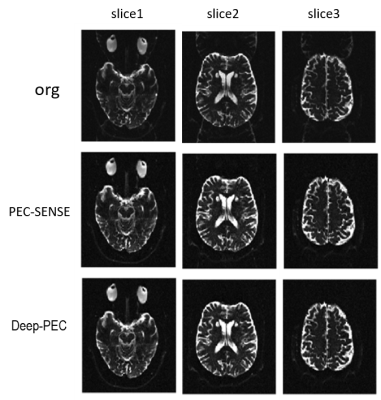
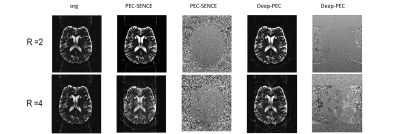
Fig2. shows the phase correction results of DWI data of volunteers. The calibration data is first extracted from center of K-space of data, which has a consistent phase with the image data. Threre is no visible ghost in both PEC-SENSE and the proposed method Deep-PEC 2-fold acceleration. Fig3. shows the results of phase correction using a real-scanned calibration data in calculation. The images corrected by PEC-Sense display more visible residual ghost than images corrected by Deep-PEC. The proposed method Deep-PEC exhibits more robustness to resist the phase mismatch between calibration data and image data. Additionally,Deep-PEC shows higher pSNR in results than PEC-SENSE,and its reconstruction time is second orders while standard sense costs several minutes.Discussion and conclusion
In this study, the deep learning is applied for EPI phase error calculation exhibited more robustness, which is insensitive to imperfect calibration data has an inconsistent distortion with the image data. The Nyquist ghost was more effectively removed in low or high-accelerated data and pSNR was comparable to that by the PEC-SENSE . Reconstruction time also is a priority.Acknowledgements
This work was supported by Shanghai Municipal Science and Technology Major Project (No.2017SHZDZX01), Shanghai Municipal Science and Technology Major Project (No.2018SHZDZX01) and ZJLab, Shanghai Natural Science Foundation (No. 17ZR1401600) and the National Natural Science Foundation of China (No. 81971583).References
1. Victor B. Xie, Mengye Lyu, Yilong Liu, Yanqiu Feng and Ed X. Wu Robust EPI Nyquist Ghost Removal by IncorporatingPhase Error Correction With Sensitivity Encoding(PEC-SENSE), Magnetic Resonance in Medicine 79:943–951 (2018)
2. Yilong Liu, Mengye Lyu, Ed X. Wu, PEC‐GRAPPA reconstruction of simultaneous multislice EPI
3. Aggarwal HK, Mani MP, and Jacob M. Modl: Model based deep learning architecture for inverse problems. IEEE Transactions on with slice‐dependent 2D Nyquist ghost correction, Magnetic Resonance in Medicine
4. Poddar S and Jacob M. Dynamic mri using smoothness regularization on manifolds (storm). IEEE transactions on medical imaging, 2016; 35:1106–1115 Medical Imaging, 2018; pages 1–1. ISSN 0278-0062.10.1109/TMI.2018.2865356
5. Schlemper J, Caballero J, Hajnal JV, Price AN, and Rueckert D. A deep cascade of convolutional neural networks for dynamic mr image reconstruction. IEEE transactions on Medical Imaging, 2018; 37:491–503u
Figures