Introduction

In single-shot EPI acquisition, the entire two-dimensional (2D) k-space data is acquired in a single RF pulse excitation. However, EPI is more sensitive to image artifacts than conventional spin-warp imaging due to the reversal of readout gradient polarities between two consecutive echoes¹. A unique artifact of EPI, termed Nyquist artifact, is caused by inconsistency between positive-readout and negative-readout ky lines. The phase inconsistency map can be obtained either directly from separately acquired reference scans² or inherently from the acquired image data itself using techniques like phase-cycled reconstruction³. However, reference scans, especially 2D reference scans, require additional scan time and may be susceptible to changes in subject position. Phase-cycled reconstruction needs a relatively large field of view (FOV) so that artifacts in the image background can be measured, which may not be feasible for EPI scans accelerated with multi-band imaging³.

Methods

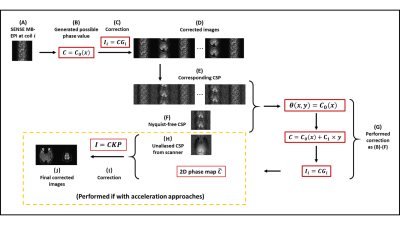
In this study, we investigated a coil-signature-based phase cycled correction method, combined with coil sensitivity profile (CSP), to remove Nyquist artifact in single-shot EPI. This method also works for single-shot EPI with MB acceleration factor ($$$Acc_{MB}$$$) and in-plane acceleration factor ($$$Acc_{in}$$$). The algorithm is outlined below:

Step 1: The phase inconsistency map was determined by using phase-cycled reconstruction and minimization of CSP differences. We first performed phase cycling along the readout-encoding direction column by column as shown in Eq.1, in which $$$C_{0}$$$ was cycled between $$$-\pi$$$ and $$$\pi$$$ in 50 steps.
$$\theta(x,y)=C_{0}(x)+C_{1}\times y $$[1]
The Nyquist artifact-free complex image signals can be obtained by solving Eq.2.
$$I=Cg$$[2]
where $$$g$$$ is a $$$2i\times1$$$ column vector with elements representing Nyquist artifact-free complex image signals of coil $$$i$$$; $$$I$$$ is a $$$2i\times1$$$ column vector with elements representing the positive and negative readout images of coil $$$i$$$; $$$C$$$ is a $$$2i\times2i$$$ matrix, with elements $$$\theta(x,y)$$$ representing phase inconsistency map intensities at location $$$(x,y)$$$.

For correction with each possible $$$C_{0}$$$ value, we generated corresponding CSPs and determined the phase value for each column with the minimum difference compared to the Nyquist artifact-free CSP, which is without Nyquist artifact but still with aliased artifacts if single-shot EPI is with different acceleration schemes. The Nyquist artifact-free CSP can be calculated based on the unaliased CSP acquired from the scanner. After the phase map along the readout-encoding direction was determined, phase cycling was performed again but this time along the phase-encoding direction as shown in Eq.1 and Eq.2, in which is cycled $$$-\pi$$$ and $$$\pi$$$ in 50 steps.

Step 2: With the phase map $$$\theta(x,y)$$$ from step 1 and the unaliased CSP, the unaliased parent-image intensity can be resolved using Eq.3 or equivalently using Eq.4 and Eq.5.
$$I=CKP$$[3]
where $$$C$$$ is the phase map $$$\theta(x,y)$$$ from step 1 and $$$K$$$ represents the unaliased CSP; $$$P$$$ represents the unaliased parent-image intensity.
$$I_{p,i}=\frac{1}{2Acc_{in}}\sum_{z=1}^{Acc_{MB}}\sum_{n=0}^{2Acc_{in}-1}K_{z,i}(x,y+\frac{n\times{FOV}}{2Acc_{in}})P_{z}(x,y+\frac{n\times{FOV}}{2Acc_{in}})$$[4]
$$I_{n,i}=\frac{1}{2Acc_{in}}\sum_{z=1}^{Acc_{MB}}\sum_{n=0}^{2Acc_{in}-1}e^{i\theta(x,y+\frac{n\times{FOV}}{2Acc_{in}})}e^{i\theta_{n}}K_{z,i}(x,y+\frac{n\times{FOV}}{2Acc_{in}})P_{z}(x,y+\frac{n\times{FOV}}{2Acc_{in}})$$[5]
where $$$K_{z,i}(x,y+\frac{n\times{FOV}}{2Acc_{in}})$$$ represents the unaliased complex CSP intensity separated by $$$\frac{FOV}{2Acc_{in}}$$$ at slice $$$z$$$ of coil $$$i$$$; $$$P_{z}(x,y+\frac{n\times{FOV}}{2Acc_{in}})$$$ represents the unaliased parent-image intensity separated by $$$\frac{FOV}{2Acc_{in}}$$$ at slice $$$z$$$; $$$\theta(x,y+\frac{n\times{FOV}}{2Acc_{in}})$$$ represents phase difference between positive-readout and negative-readout image separated by $$$\frac{FOV}{2Acc_{in}}$$$ and $$$\theta_{n}$$$ is known as priority, which is caused by the k-space acquisition trajectories. Eq. 4 and Eq. 5 have $$$2Acc_{in}$$$ unknown variables and they can be resolved if the number of coils $$$i>2Acc_{in}$$$. Figure 1 shows the workflow of correction for SENSE MB-EPI with $$$Acc_{in}=2$$$ and $$$Acc_{MB}=2$$$. In Figure 1, steps in yellow box were performed if single-shot EPI are with acceleration approaches.

Results

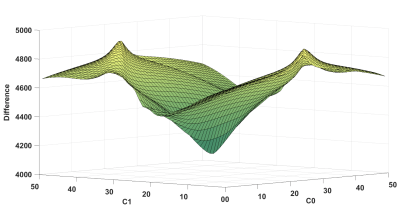
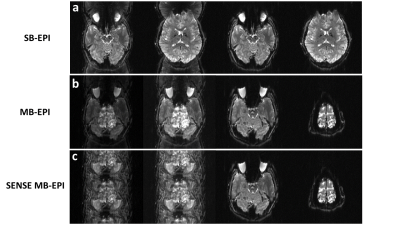
Figure 2 shows the CSP differences, reconstructed with 50 different phase gradient values along each of the directions and compared to the unaliased CSP. It can be found that the CSP difference is a minimum only when the chosen phase gradient values match the phase inconsistency. Figure 3 shows the aliased images and corresponding corrected images for SB-EPI, MB-EPI ($$$Acc_{MB}=2$$$) and SENSE MB-EPI ($$$Acc_{MB}=2,Acc_{in}=2$$$). Both the Nyquist artifact and aliased artifacts caused by different acceleration schemes are effectively eliminated.

Discussion

In our study, we demonstrated that our novel 2D coil-signature-based phase-cycled reconstruction method can successfully reduce Nyquist artifact in single-shot EPI integrated with various in-plane and through-plane acceleration schemes. This technique can be further extended to multi-shot EPI.

Acknowledgements

No acknowledgement found.