3415
Compensating Diffusion Bias of Quantitative T2 mapping on High-Field MRI Scanners
Natalie Bnaiahu1, Ella Wilczynski1, Shir Levy2, Noam Omer1, Tamar Blumenfeld-Katzir1, and Noam Ben-Eliezer1,3,4
1Biomedical Engineering, Tel Aviv University, Tel Aviv, Israel, 2School of Chemistry, Tel Aviv University, Tel Aviv, Israel, 3Sagol school of Neuroscience, Tel Aviv University, Tel Aviv, Israel, 4Center for Advanced Imaging Innovation and Research, New York, NY, United States
1Biomedical Engineering, Tel Aviv University, Tel Aviv, Israel, 2School of Chemistry, Tel Aviv University, Tel Aviv, Israel, 3Sagol school of Neuroscience, Tel Aviv University, Tel Aviv, Israel, 4Center for Advanced Imaging Innovation and Research, New York, NY, United States
Synopsis
On high-field scanners, strong imaging gradients induce spurious diffusion signal decay, which distorts qT2 calculation. By modeling the pulse sequence gradients and coherence pathways, an effective b value was calculated to assess signal attenuation caused by diffusion. ADC values were measured, extensive phantom scans and in-vivo experiments were performed using the MSME protocol with varied voxel sizes to examine the effect and the solution. Before correction T2 values were short with high variability across different voxel sizes, after correction T2 values increased and became more accurate and consistent. Tissue properties also influenced the correction as their ADC varies.
Introduction
High-field preclinical scanners employ considerable imaging gradients to achieve suitable spatial resolutions. These high gradient values result in spurious diffusion weighting and attenuation of the signal, particularly in multi spin-echo (MSE) sequences where the effect accumulates along the echo train. Thus, accurate T2 mapping involves tackling both diffusion-related underestimation of T2 values, and the acknowledged problem of stimulated and indirect echoes, which distort MSE signals. In addition, different scan parameters, especially those relating to voxel size, will produce different diffusion and stimulated-echoes signal bias, leading to highly inconsistent results. Previously we introduced a preliminary, formula-based design, for correcting diffusion bias, while employing the EMC algorithm1 to simulate the effect of stimulated echoes on the T2 decay curve.In this work, we present a significant improvement to the diffusion correction, which is now applied to each of the coherence pathways which make up the signal. This improvement offers higher accuracy and reproducibility in T2 values, even for long T2 values and extremely small voxel sizes.
Methods
An effective b-value2,3 was calculated for MSE signals based on the pulse sequence scheme and its specific imaging gradients. b-value was evaluated per echo based on the subset of coherence pathways that contributed to the signal4, thus incorporating the effects of stimulated echoes in the assessment of diffusion attenuation.$$b-value=γ^{2}\int_{0}^{t}\left(\begin{array}{c}\int_{0}^{t'} g_{x,y,z}^{*}t''dt''\end{array}\right)^{2}dt'$$
A phantom, containing 7 concentrations of MnCl2 ranging from 0.02 to 0.5 mM, was scanned on 9.4T Bruker Biospin. Spectroscopic (Hahn) spin-echo was performed to achieve ground truth T2 values. Conventional single SE (SSE) and MSE sequences were used to image the phantom with varying parameters, especially in-plain resolution and slice thickness. Diffusion coefficient was found to be close to diffusion coefficient of water at 25°C, 2.29 x 10-5 cm2/s. SSE T2 values were fitted exponentially and MSE data was fitted using the EMC algorithm – before and after applying diffusion correction.
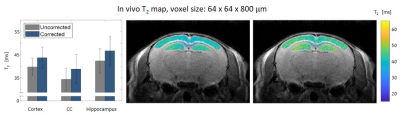
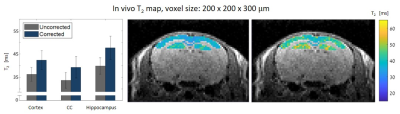
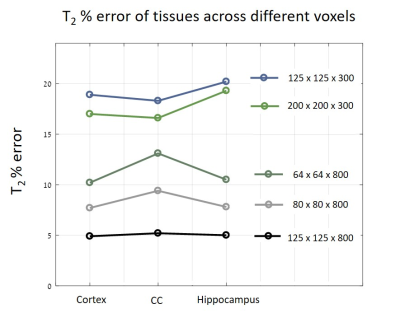
An in-vivo scan of a healthy mouse brain was imaged on a 7T Bruker Biospec using conventional DTI-EPI and MSME protocols. ADC values along different directions were extracted. A series of MSE scans was performed with different voxel sizes: 64x64x800, 80x80x800, 100x100x800, 125x125x800, 150x150x800, 125x125x300 and 200x200x300 μm3. Three brain segments were examined: the cortex, corpus callosum and the hippocampus.
Results
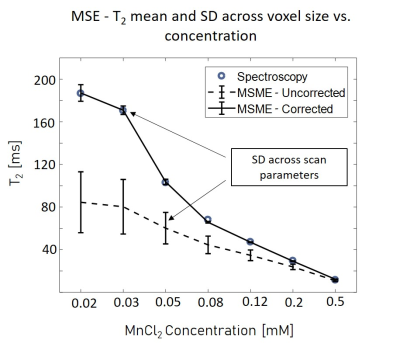
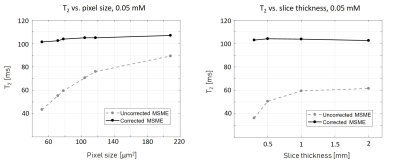
Figure 1 shows the MRS T2 values and the various MSE averaged T2 values and standard deviations, representing the variance across scans with different parameters (mainly resolution and slice thickness) per tube. For example, in the 52 μm pixel scan, the highest T2 error was 70%, found in the lowest concentration tube. In the physiological range, T2 errors were as high as 50%. After diffusion correction, T2 values of the MSE and MRS were in agreement with maximal error of 4%.In vivo results, before diffusion correction, varied in accordance with the chosen resolution / slice thickness. Thin slices voxels showed greater signal loss due to diffusion than voxels with thicker slices, even when the in plain resolution was significantly higher. The highest deviation, more than 20%, was found in the narrowest voxel and not in the overall smallest voxel. Figure 5 shows the T2 error (compared to the uncorrected value) across different voxels.
Discussion
Diffusion effect leads to significant underestimation of T2 values on preclinical scanners. Moreover, this bias is subjected to the chosen resolution, slice thickness, bandwidth, refocusing RF pulses and the sample’s diffusion coefficient along different directions. Because the effect of diffusion is accumulative, it increases with each echo and has higher influence on longer T2 values. Our results show that decreasing slice thickness leads to greater signal loss than increasing in-plain resolutions. The error also varies among tissues: narrow slices had the most significant error in T2 values in the hippocampus, whereas in voxels with high in-plain resolution the most extensive error was found in the CC. That is because both tissue's composition and geometry influence ADC values, in addition to gradients amplitudes, different tissues would undergo different T2 corrections.Conclusion
Correction is necessary for high-field / high-resolution qMRI as imaging gradients intensify the influence of diffusion, which attenuate the signals and lead to miscalculations of qT2. Effective b-value was modeled and calculated based on the MSME pulse sequence and refocusing RFs’ coherence pathways. This method is generalized and can be applied to different pulse sequences. The suggested solution improves accuracy, reduces the variability across scan settings, and provides reproducible T2 values.Acknowledgements
ISF Grant 2009/17References
1. Ben-Eliezer N, Sodickson DK, Block KT. Rapid and accurate T2 mapping from multi-spin-echo data using bloch-simulation-based reconstruction. Magn Reson Med. 2015;73(2):809-817.
2. Abragam A. The Principles of Nuclear Magnetism. Oxford: Oxford Press; 1961.
3. Torrey HC. Bloch Equation with Diffusion Terms. T Rev. 1956;104(3):563-565.
4. Hennig J. Multiecho imaging sequences with low refocusing flip angles. J Magn Reson. 1988;78(3):397-407.
Figures
Figure 1. T2
values acquired from MRS and MSE data of a phantom containing tubes with MnCl2
concentrations ranging from 0.02 mM to 0.5
mM. The blue circles indicate the spectroscopy results, the dashed line shows results before correcting diffusion effects and the solid line shows
the results after diffusion correction. The bars represent the SD across scans with different parameter sets (i.e. varied resolutions, slice thickness and
BW).
Figure 2. Phantom T2 values
acquired from MSE data of 0.05 mM MnCl2 concentration. Left panel: T2 vs. squared pixel size of 52, 71, 78, 104, 117 and 208 μm2. Right panel: T2 vs. slice thickness: 0.3, 0.5, 1 and 2 mm. The dashed line shows the uncorrected
results, the solid line shows T2 post diffusion correction. Spectroscopy results: T2 = 102.9 ms.
Figure 3. In vivo mouse brain with T2 maps of the
cortex, corpus callosum and the hippocampus, voxel size: 64 x 64 x 800 μm3. Both maps were fitted using
the EMC algorithm, before correcting diffusion effects (middle) and after diffusion correction (right). The left figure shows the averaged T2 values and SD in three segmented areas before and after diffusion correction.
Figure 4. In vivo mouse brain with T2 maps of the
cortex, corpus callosum and the hippocampus, voxel size: 200 x 200 x 300 μm3. Both maps were fitted using
the EMC algorithm, before correcting diffusion effect (middle) and after diffusion correction (right). The left figure shows the averaged T2 values and SD in three segmented areas before and after diffusion correction.
Figure 5. T2 error (compared to the uncorrected value) in different voxels. Thinner slices
expressing higher errors in general, especially in the hippocampus. Higher
in-plain resolution leads to relatively high errors in the CC. Voxel sizes: 125 x 125 x 300, 200 x 200 x 300, 64 x 64 x 800, 80 x 80 x 800 and 125 x 125 x 800 μm3.