Background and Purpose

Nyquist ghosting is a common artifact in echo planar imaging (EPI)^1-3 caused by: 1) readout gradient-induced low-order eddy currents; and 2) receive chain imperfections (e.g., group delay). These effects impose phase modulations of which polarity alternates with readout direction (i.e., even or odd), which causes ghost artifacts to appear at half field-of-view (FOV) intervals. Ghost artifacts degrade image interpretability and compromise quantitative measurement validity^4,5. The Nyquist ghost related to low order concomitant fields may be compensated in realtime^6,7. In practice, although single-polarity reference scan-based paradigms are routinely used to combat Nyquist ghosting, they often fail to the fully suppress them because of statistical biases in estimated correction coefficients that result from noise and off-resonance effects. Prior work^3,8-10 has shown that use of dual polarity reference scans can mitigate the latter. In this work, we propose that this concept can be generalized to enable robust Nyquist ghost correction (NGC) directly from two reversed readout EPI acquisitions – without explicit reference scanning. We derive a model-based process for directly estimating statistically optimal NGC coefficients from multi-channel k-space data, present robust and efficient numerical procedures for performing this task, and experimentally demonstrate its corrective advantages.

Methods

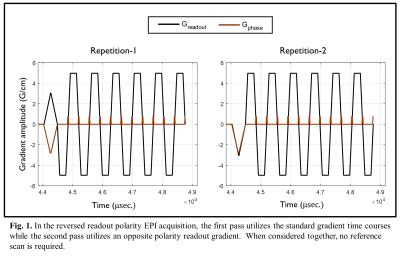
I. Reverse Readout EPI Acquisition: A reverse readout polarity EPI acquisition comprises performing two phase-encoded EPI acquisitions, whose readout gradient polarities have opposite sign at onset (see Fig. 1). After temporally Fourier transforming the raw EPI dataset (before ramp resampling, if needed) along the readout direction, the m^th sample of the n^th readout line of an EPI acquisition can be modeled as:
$$g_{n,\pm}[m,c]=H_{n,\pm}(\alpha,\beta)[m]f_n[m,c]+\epsilon_{n\pm}[m,c]---(1)$$
where c is the coil index, "$$$\pm$$$" denotes readout gradient polarity, $$$H_{n,\pm}[m]=e^{\pm(-1)^nj(\alpha{m}+\beta)}$$$ is the system response function, $$$\alpha$$$ and $$$\beta$$$ are the unknown system coefficients⁹, is the actual k-space signal, and $$$ε_{\pm}$$$ is zero-mean Gaussian noise with (CxC) coil covariance $$$\Psi$$$ . The reversed readout data set can be written in ensemble (2MxC) as:
$$g_n=\begin{bmatrix}g_{n,+}\\g_{n,-}\end{bmatrix}=\left(I\otimes\begin{bmatrix}H_{n,+}(\alpha,\beta)\\H_{n,-}(\alpha,\beta)\end{bmatrix}\right)f_n+\begin{bmatrix}\epsilon_{n,+}\\\epsilon_{n,-}\end{bmatrix}---(2)$$
where $$$\xi=[\alpha\quad\beta]^T$$$ and $$$\otimes$$$ is Kronecker’s product.
II. Proposed System Delay Estimation: The system coefficient vector $$$\xi$$$ and unmodulated k-space signal $$$f$$$ can be determined from (2) via maximum likelihood (ML) estimation, which comprises solving:
$$\mathop{\min}_{f\in\mathbb{C},\xi\in\mathbb{R}}\left\{J(f,\xi)\triangleq\sum_{n=1}^{N}\sum_{c=1}^{C}\left\Vert\Phi_n(\xi)f_{n,c}-g_{n,c}\right\Vert^2_{\psi^{-1}}\right\}---(3)$$
The optimizing k-space signal estimate is $$$f_n=\frac{1}{2}\Phi^*_n(\xi)g_n$$$ , where “*” denotes the Hermitian transpose. Variable Projection¹¹ (VARPRO) of $$$f$$$ into $$$J(\cdot)$$$ reduces the dimensionality of (3) to:
$$\mathop{\min}_{\xi\in\mathbb{R}}\left\{J(\xi)\triangleq\sum_{n=1}^{N}\sum_{c=1}^{C}\left\Vert(\frac{1}{2}\Phi_n(\xi)f_{n,c}-I)g_n\right\Vert^2_{\psi^{-1}}\right\}\equiv\sum_{m=1}^{M}|u[m]|cos\Big(2\delta^T _m B \xi-\angle u[m]\Big)---(4)$$
where $$$\delta_m$$$ denotes Kronecker’s delta, B is an Mx2 Vandermonde submatrix, $$$K_n=g_{n,+}\Psi^{-1}g_{n,-}$$$ , and the sufficient statistic $$$u[m]=\sum_{n,even}K_n[m,m]+\sum_{n,odd}\overline{K_n[m,m]}$$$ . Minimizers of this non-convex cost can be found by preconditioned gradient descent:
$$\xi_{t+1}=\xi_t-P^{-1}\triangledown{J(\xi)}---(5)$$
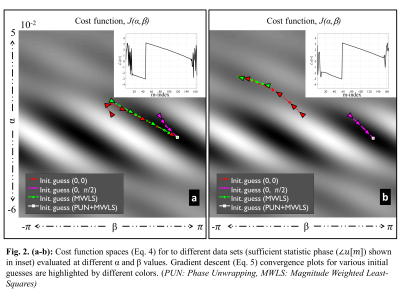
with dense preconditioner $$$P=4B^T(\sum_m|u[m]|\delta_m\delta^T_m)B$$$ , using the magnitude weighted least squares (MWLS) approximation of (4) applied to $$$\angle{u}$$$ following 1D phase unwrapping (PUN) as an initial estimate. Following estimation of $$$\xi$$$ , $$$f$$$ is readily determined using the above expression.
III. Data Acquisition and Image Reconstruction: Two healthy volunteers were imaged under an IRB-approved protocol on a compact 3T-MRI system¹²: (G_max=80mT/m, SR=700T/m/s), with C=32 receive-only brain coil. Both standard (forward-only; NEX=2) and reverse readout gradient polarity (forward+reverse) EPI acquisitions were performed for the comparison. The standard raw datasets were averaged before NGC using the vendor pipeline¹³. For the reverse readout acquisition, the unmodulated raw dataset was estimated via the above described approach. Images from both result sets were then reconstructed via root-sum-of-squares (RSS) or SENSE for acceleration factors R=1 and R={2, 3}, respectively.

Results

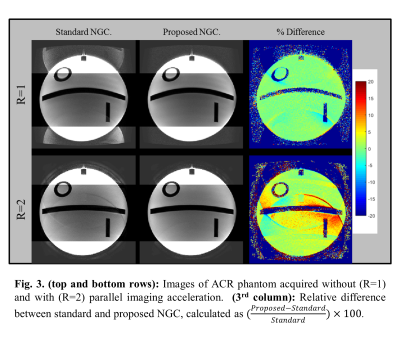
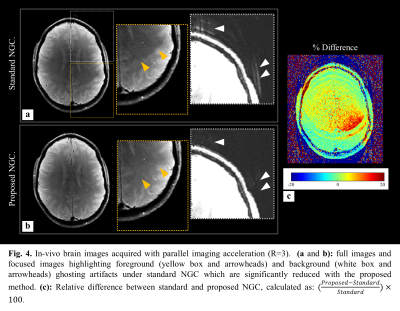
Figures 2a,b depict two example non-convex cost function spaces ($$$J(\xi)$$$) , which contain many local and global extrema. The pre-PUN sufficient statistic $$$\angle{u[m]}$$$ are shown in the subfigures. Overlaid convergence plots (color) demonstrate the impact of initial guess selection on convergence rate and attraction. Utilizing the MWLS result for the unwrapped sufficient statistic (PUN+MWLS) provides rapid convergence to (non-unique) global minima, as compared to the non-unwrapped MWLS and fixed-value initializations $$$(0,\pi)$$$. Figure 3 shows strong residual Nyquist ghost artifacts the phantom images generated with the standard acquisition and vendor NGC. For R=1, these artifacts are dominant in the background region whereas for R=2 they are dominantly in the foreground, the latter being due to error propagation through SENSE unfolding. In contrast, the proposed reverse readout acquisition and NGC method largely mitigates these artifacts at both acceleration rates. In Figure 4, in-vivo results (R=3) show the similar trends as in phantom examples, with the proposed NGC paradigm mitigating aliasing artifacts representing up to 20% intensity errors.

Discussions

The proposed NGC acquisition and reconstruction paradigm provides superior artifact mitigation relative to the standard method in both phantom and in-vivo brain experiments, and across acceleration rates. This is directly attributable to the improved noise management and prospective avoidance of off-resonance biases in the proposed approach. Although this paradigm requires a two-pass acquisition, we anticipate that it can be combined with higher acceleration factors or incorporated into multi-pass EPI sequences (e.g., diffusion weighted imaging (DWI)) to minimize or eliminate additional overhead above conventional setups. With appropriate generalization, this robust physics-driven paradigm could potentially serve as a platform for managing complex ghosting artifacts due to anisotropic gradient delays, cross-term and higher-order readout eddy currents, as well as encoding gradient eddy currents (e.g., diffusion lobes). The performance of the proposed setup may also be further improved through use of target-dependent regularization or constraints, such as minimum entropy regularization¹⁴ or linear predictability¹⁵.

Acknowledgements

This work was supported by NIH U01 EB024450.