Purpose:

The use of spiral imaging has drawn more attention in clinical application due to its high SNR efficiency and being less prone to motion^1-3. Image blurring due to off-resonance in spiral acquisition still remains a challenge. Inaccuracies in field map estimation may degrade the quality of image deblurring approaches^4-6. The present work proposed a self-reference model to estimate the discrepancies of the field between the image data and the pre-acquired field estimation to improve the image quality for the two-point Dixon spiral acquisition.

Theory:

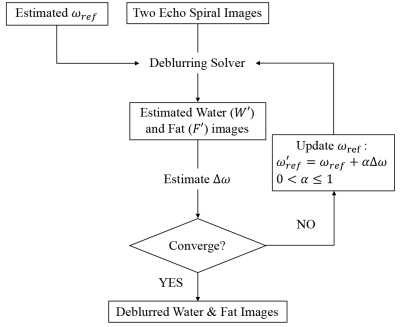
Both water and fat signals are assumed in-phase at TE = 0. The signals at two different echo times can be modeled by $$ S_1 = e^{j\theta}(W+F\Psi_1)e^{j \omega_0{TE}_1}, and $$ $$ S_2 = e^{j\theta}(W+F\Psi_2)e^{j \omega_0 {TE}_2} $$ ,where $$$ W $$$ and $$$ F $$$ are both real numbers, $$$ \theta $$$ is the underlying object phase, $$$\Psi_1$$$ and $$$ \Psi_2 $$$ are modeled normalized fat signals at $$$ {TE}_1 $$$ and $$$ {TE}_2$$$ respectively, and $$$ \omega_0 $$$ is the resonant frequency or the field map. The two-point Dixon algorithm estimates water ( $$$ W' $$$ ) and fat( $$$ F' $$$ ) components in terms of a reference resonant frequency $$$ \omega_{ref} $$$ as: $$ W' = (\Psi_2 - \Psi_1)^{-1} (\Psi_2S_1e^{-j \omega_{ref}{TE}_1} - \Psi_1S_2e^{-j \omega_{ref}{TE}_2}), and $$$$ F' = (\Psi_2 - \Psi_1)^{-1} (S_2e^{-j \omega_{ref}{TE}_2} - S_1e^{-j \omega_{ref}{TE}_1}). $$ Rewriting $$$ W'$$$ and $$$ F' $$$ as $$ W'+F'\Psi_1 = e^{j\theta}(W+F\Psi_1)e^{j \Delta \omega{TE}_1}, and $$ $$ W'+F'\Psi_2 = e^{j\theta}(W+F\Psi_2)e^{j \Delta \omega{TE}_2}$$, one can assess the mismatch between the frequencies, $$$ \Delta \omega \equiv \omega_0 - \omega_{ref} $$$. Accordingly, the field difference becomes $$ \Delta \omega = {1 \over {({TE}_2 - {TE}_1)}} arg({{(W'+F'\Psi_2) \bullet conj(W'+F'\Psi_1)} \over {(W+F\Psi_2) \bullet conj(W+F\Psi_1)}}) $$ with two unknown variables $$$ W $$$ and $$$ F $$$. These two variables can be approximated by $$$ |W'| $$$ and $$$ |F'| $$$respectively as the equality holds at $$$ \Delta \omega = 0 $$$. In practice, an iterative processing is applied to keep updating $$$ \omega_{ref} $$$ as well as both $$$ W' $$$ and $$$ F' $$$ as shown in Fig. 1 until reaching the convergence criterion. The amount to update $$$ \omega_{ref} $$$ is controlled by a relaxation parameter $$$ \alpha $$$ to prevent from divergence due to noise or numerical error. An empirical value $$$ \alpha = 0.5 $$$ was adopted in this work as far as speed and stability in computation was concerned.

Materials and Methods

Volunteer studies were conducted on a 3.0T scanner (Ingenia Elition, Philips, Best, Netherlands) with informed consent. Four participants were enrolled for the head scan and the other four for the abdominal scan. The image sequences and the corresponding parameters are listed in Table 1. A separate scan for $$$ \omega_{ref} $$$ estimation was performed ahead of the image acquisition. An additional 60 Hz offset was added to the pre-acquired field map to simulate error estimation. The image data along with the offset field map were reconstructed with the proposed iterative algorithm. The convergence criterion was set when the difference between the reconstructed images of two consecutive iterations.

Results

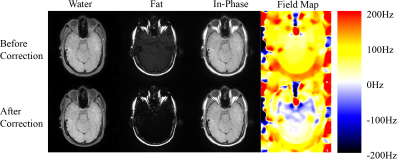
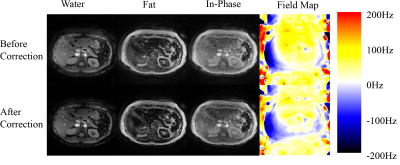
Figures 2 and 3 demonstrate the results from a head scan and an abdominal scan from two different volunteers. Significant blurring exhibits over different parametric images as well as misplacement of fat and water signals (Figs. 2 and 3 upper row). This blurring effect becomes diminishing after updating the field map (Figs. 2 and 3 lower row). In the head scan, better gray matter and white matter structure along with sharper delineation of the extraocular muscles appears in the water image after correction (Fig. 2). The optic nerve tracts are also more apparent in the in-phase image. The edges of the vessels in the abdominal scan (Fig. 3) become better outlined from the parenchyma with the corrected field map. The abdominal cage as well as the edge of the internal organs become well defined in the water and in-phase images in addition to improved component separation. The field maps before and after correction in both scans demonstrate consistent quantitative differences with the added value in the error simulation.

Discussions

An iterative method to update field map is proposed in the present work to improve deblurring of fat and water spiral image. The results suggest that the proposed method can mitigate blurring by improving the accuracy of the off-resonance values in different anatomies. Although the range of frequency offsets the algorithm can correct has not been examined here, error is likely to occur if the offset exceeds the chemical shift between fat and water. Thus, this algorithm is not entirely autofocused, and a reasonable field map estimation and good shimming still play essential roles in the final image quality. With these in place, the proposed method should be capable of updating the field map for all the subsequent scans in the same experiment.

Conclusions

A semi-autofocus algorithm to update the field map for two-point Dixon spiral imaging was proposed and tested in the present work. This algorithm features correcting fat-water swap and minimizing blurring artifact by updating the field map from the image data and an approximate field map reference.

Acknowledgements

This work was funded in part by Philips Healthcare.