Introduction

Field gradients for imaging and diffusion encoding exhibit non-linearity (GNL). This non-linearity affects both the strength and direction of diffusion encoding, i.e., it perturbs the B-matrix a.k.a. the B-tensor (1). This error can be corrected by mapping the actual B-tensor field as a function of position, and accounting for it in subsequent analysis. However, when asymmetric gradient waveforms are used, for example for efficient tensor-valued diffusion encoding, GNLs may also affect the delicate compensation for concomitant gradients, or the so called 'Maxwell compensation' (2). In that case, the concomitant gradients cause a residual dephasing vector at the end of the encoding which may corrupt the measured signal and confound the analysis (2,3).
$$$~~~~~$$$The aim of this study was to investigate how GNLs affects Maxwell-compensated asymmetric gradient waveforms. We demonstrate the effects at the Connectom system, where ultra-high gradient amplitudes and severe non-linearities exacerbate the concomitant gradients and their impact on signal accuracy.

Methods

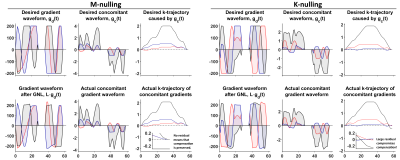
The field gradient produced by each coil is specific to its geometry and can be measured or obtained from the vendor. The departure from ideal linear gradients can be described by spatially-varying "gradient coil tensors" $$$(\mathbf{L})$$$ which are calculated from the spatial partial derivative of the effective fields (1). In general, GNLs become more severe as the size of the coil is reduced, inflating the problem for, for example, insert gradient coils.
$$$~~~~~$$$Gradient waveforms for tensor-valued diffusion encoding can be optimized using two different types of Maxwell compensation, namely socalled M- and K-nulling (2). Briefly, $$$\mathbf{M}$$$ and $$$\mathbf{K}$$$ are matrices that capture the magnitude of the concomitant gradients, calculated from the desired gradient waveform $$$(\mathbf{g}_\mathrm{d}(t)=[g_x(t)~g_y(t)~g_z(t)]^T)$$$, according to (2)
$$\mathbf{K}\propto\int_0^{\tau}~h(t)\begin{bmatrix}g_z^2(t)&0&-2g_x(t)g_z(t)\\0&g_z^2(t)&-2g_y(t)g_z(t)\\-2g_x(t)g_z(t)&-2g_y(t)g_z(t)&4g_x^2(t)+4g_y^2(t)\\\end{bmatrix}\mathrm{d}t$$
and
$$\mathbf{M}\propto\int_0^{\tau}~h(t)\begin{bmatrix}g_x^2(t)&g_x(t)g_y(t)&g_x(t)g_z(t)\\g_y(t)g_x(t)&g_y^2(t)&g_y(t)g_z(t)\\g_z(t)g_x(t)&g_z(t)g_y(t)&g_z^2(t)\\\end{bmatrix}\mathrm{d}t$$
where integration is over the duration of the diffusion encoding, $$$t$$$ is time, and $$$h(t)$$$ is a function that shows the direction of spin dephasing. We note that both matrices are proportional to the square of the gradient waveform, showing that the problem increases with increasing gradient amplitude. If $$$\mathbf{M}$$$ and $$$\mathbf{K}$$$ are zero, the effect of concomitant gradients is negligible. Nulling $$$\mathbf{M}$$$ during waveform optimization ensures negligible effects from concomitant gradients (Maxwell compensation) for arbitrary rotations of the waveform, whereas nulling $$$\mathbf{K}$$$ is more efficient, but does not allow for arbitrary rotation. Since spherical encoding does not require rotations, this restriction is circumvented, facilitating the highest efficiency for K-nulling.
$$$~~~~~$$$We estimate the impact of GNL on the Maxwell compensation by simulating imperfect gradient waveforms using gradient coil tensors from the Connectom system (4). After optimizing the desired gradient waveform $$$(\mathbf{g}_\mathrm{d})$$$ tailored to the system (2,5), the actual gradient waveform $$$(\mathbf{g}_\mathrm{a})$$$ is calculated as $$$\mathbf{g}_\mathrm{a}(\mathbf{r},t)=\mathbf{L}(\mathbf{r})\mathbf{g}_\mathrm{d}(t)$$$ at position $$$\mathbf{r}$$$ (1). The signal error is estimated in the 'concomitant gradient analysis toolbox' (2,6,7) assuming a spin-echo with EPI readout using the parameters detailed in Table 1.

Results

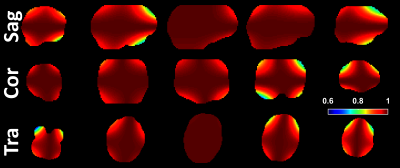
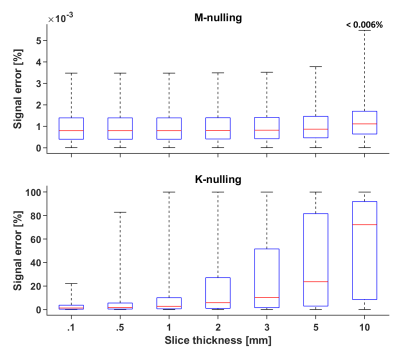
Figure 1 shows gradient waveforms optimized using M- and K-nulling; both are Maxwell-compensated in the absence of GNLs because the desired concomitant gradient waveform has a residual k-vector with negligible magnitude at the end of the encoding. However, when non-linearity is introduced, the Maxwell compensation is preserved for M-nulling, but not for K-nulling. Figure 2 shows the expected signal error caused by concomitant gradients in a brain-shaped volume centered on the iso-center. The error increases further away from the iso-center, and reaches 30% signal loss approximately 9 and 6 cm from the iso-center for a slice thickness of 2 and 5 mm, respectively. Figure 3 shows that K-nulling is likely to suffer marked errors throughout the FOV, especially for thicker slices, whereas M-nulling is immune to concomitant field effects caused by GNLs.

Discussion and conclusions

We demonstrate that gradient non-linearity compromises Maxwell compensation when K-nulling is used, whereas M-nulling is immune to the perturbation. Therefore, we recommend M-nulling for any MRI system that suffers prominent gradient non-linearity and/or uses high gradient amplitudes. Since the signal error depends on a wide range of system, imaging, waveform and object parameters we suggest that the impact of GNLs be predicted in simulations; this investigation is enabled by methodology and tools found in refs. (2,4,7). We expect that this effect is smaller at conventional MRI systems, however, it will remain especially relevant as the dMRI field pushes toward ever higher gradient amplitudes and compact coil designs.

Acknowledgements

We acknowledge the following research grants NIH P41EB015902, NIH R01MH074794. This study was supported by grants from Swedish Research Council (2016-03443). MP is supported by a NSERC scholarship (PDF-502732-2017) from Canada. CE and MP are supported by the SPP2041 program "Computational Connectomics" of the German Research Foundation (DFG).