3390
Data-Driven non-Cartesian trajectory correction based on Cartesian reference data1Siemens Healthcare, Erlangen, Germany
Synopsis
Trajectory deformations in non-Cartesian scans can lead to significant image artifacts, while in comparison the effect on Cartesian scans is evidentially minor. We propose a novel approach for trajectory correction relying on the minimization of a suitable measure between a non-Cartesian image and a Cartesian reference image, given a trajectory deformation model. Our proof of concept is applied on simulated as well as measured data. The approach is fast, accurate and easily extendable. Given the right use-case, no extra scan time is required (e.g. mixed spiral-Cartesian MR Fingerprinting).
Introduction
Nominal and realized k-space trajectories in MRI differ due to imperfections of the gradient system. Major effects influencing the realized trajectories are gradient delays and eddy currents1-5.Various approaches for correcting gradient imperfections exist, both on the hardware6-9 and on the acquisition or post processing side. The former focus on shielding gradient coils, thereby reducing eddy current effects. On the acquisition side - in addition to appropriate gradient design24-26 - realized trajectories can be measured2,3,10-18. Other calibration methods determine parameters of a model derived from the gradient impulse response function (GIRF)1,12,19-21. In order to be practical, the latter methods are designed to be calibrated once per scanner in isolated experiments, assuming the determined parameters to be constant over time and consistent for any setup. This assumption is unlikely to fully hold, considering that some effects cannot be covered in the calibration, e.g. the applied gradients and the temperature differ. In contrast, the gradient delay can be determined per measurement22,23.
Evidently, Cartesian scans do not suffer substantially from trajectory deformation: In case of gradient delays, the sampling pattern is shifted uniformly in k-space, resulting in a phase in image space. The effect of eddy currents is minimal, since the gradients are applied in the same direction and are constant during readout.
This does not hold for non-Cartesian scans27, leading to severe image artifacts. As a result of the beforehand described limits of existing calibration techniques, visible effects of trajectory deformation can remain, reducing the robustness and acceptance of non-Cartesian scans in clinical applications.
We propose a novel trajectory correction approach for non-Cartesian scans relying on the fact that the image quality of Cartesian scans is less prone to gradient imperfections.
Methods
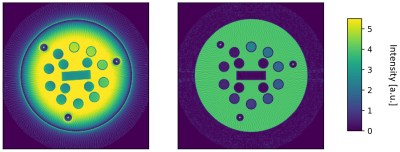
Other Trajectory CalibrationsWe compared a Cartesian slice of the NIST phantom39 with spiral images of the same object acquired with a prototype sequence, where different trajectories were employed in the reconstruction: The nominal as well as the corrected ones according to Tan et al.1 and Berzl et al.21, both non-scanner-specific.
Our Prototype Correction Method
A comparison of Cartesian and non-Cartesian scans provides information for trajectory correction. A suitable measure can be defined to quantify their similarity, which is assumed to be maximal if the trajectory is correct. Given a trajectory deformation model, our approach is to optimize the parameters of this model with respect to the measure, which is possible since every operation performed in the reconstruction is differentiable. If the reference scan data can be used apart from the trajectory correction, no extra scan time is required.
Reconstruction of Non-Cartesian Data
Non-Cartesian scans can be reconstructed using the fast non-uniform Fourier transform (NUFFT)28-31. It encompasses gridding the data, prior to applying the FFT, finally correcting for the gridding by dividing by the kernel’s Fourier transform and applying a sampling density compensation32, 33.
Trajectory Deformation Model
We propose to use the GIRF as a physically meaningful model. Hereby it is assumed that the realized gradient $$$g$$$ depends linearly on the nominal gradient $$$\hat{g}$$$:
$$g(t)=\int_{\mathbb{R}}\chi(t-t')\cdot\hat{g}(t')\,dt'$$.
According to Tan et al.1, a simple model regarding gradient delay and eddy currents is given by34:
$$\chi(t)=\theta(t)\cdot\sum_{n}\,a_n\cdot e^{-b_n\cdot(t-t_0)},$$
where $$$\theta$$$ is the step function.
Implementation
We used python3, Tensorflow35 and the ADAM optimizer36.
Simulation
We applied our approach to an artificial slice of the NIST phantom. An Archimedean spiral trajectory was deformed according to the proposed GIRF model (single $$$n$$$). Starting with a different choice of parameters, the optimization was performed by minimizing the mean absolute error between the cartesian and the spiral image.
Application to Real Data
A crucial point is an adequate similarity measure, since the Cartesian and spiral scans exhibit different contrasts (e.g. Fig. 1). We normalized images reconstructed from real measured data to [0, 1] and applied a Sobel edge filter. The optimization was set up to minimize the difference between the edge images.
Results
Other Trajectory CalibrationsFig. 1 and 2 show that both correction methods can fail to remove artifacts in spiral images in this exemplary case.
Simulation
The reconstruction with the nominal trajectory exhibits significant artifacts and rotation (Fig. 3, left), the initial difference measure is visualized in Fig. 4, left side. The optimization converged towards the employed parameters of the GIRF model, resulting in a final reconstruction that matches the ground truth, besides undersampling artifacts (right sides of Fig. 3 and 4).
Application to Real Data
The optimization effectively minimized the difference of the measured Cartesian and Spiral edge images (Fig. 5).
Discussion
Our experiments show that existing calibration methods can fail due to lacking adaptability. We demonstrate that using Cartesian reference scans for a data driven calibration of non-Cartesian k-space trajectories is possible. Future research will concentrate on finding suitable difference measures, quantifying effects of trajectory deformation in images of different contrasts.Conclusion
The proposed trajectory deformation model is extendable, effects beside gradient delay and eddy currents can be introduced. No static calibration is necessary, our method can adapt to temporal deviations of the scanner. It relies on the comparison in image domain, which is the actual subject of interest. Given a suitable use-case, e.g. MR Fingerprinting (MRF)37, 38 with mixed spiral and Cartesian readouts, no extra scan time is required.Acknowledgements
We thank Josef Pfeuffer for inspiring discussions.References
1. Tan H., Meyer C. H. (2009). Estimation of k‐space trajectories in spiral MRI. Magn. Reson. Med., 61: 1396-1404. doi:10.1002/mrm.21813
2. Ding X., Tkach J., Ruggieri P., Perl J., Masaryk T. (1997). Improvement of spiral MRI with the measured k‐space trajectory. J. Magn. Reson. Imaging, 7: 938-940. doi:10.1002/jmri.1880070525
3. Mason G. F., Harshbarger T., Hetherington H. P., Zhang Y., Pohost G. M. and Twieg D. B. (1997). A Method to measure arbitrary k‐space trajectories for rapid MR imaging. Magn. Reson. Med., 38: 492-496. doi:10.1002/mrm.1910380318
4. Liu Q., Hughes D. G., Allen P. S. (1994). Quantitative characterization of the eddy current fields in a 40‐cm bore superconducting magnet. Magn. Reson. Med., 31: 73-76. doi:10.1002/mrm.1910310112
5. Spielman D. M., Pauly J. M. (1995). Spiral imaging on a small‐bore system at 4.7t. Magn. Reson. Med., 34: 580-585. doi:10.1002/mrm.1910340414
6. Morich, Michael A. (1994). MRI Self-Shielded Gradient Coils, US Patent 5,296,810
7. Mulder Gerardus B. J., Ham Cornelis L. G., Mateboer Aart J., Roozen Nicolaas B., Verbunt Johannes P. M. (2001). MRI Apparatus with a Mechanically Integrated Eddy Current Shield in the Gradient System, US Patent US 6,326,788 B1
8. Crozier Stuart, Doddrell David M. (1995), A design methodology for short, whole-body, shielded gradient coils for MRI, Magnetic Resonance Imaging, Volume 13, Issue 4, Pages 615-620, ISSN 0730-725X
9. DeMeester Gordon D., Morich Michael A., Shvartsman Shmaryu M. (2002). Efficiently Shielded MRI Gradient Coil with Discretely or Continuously Variable Field of View, US Patent US 6,479,999 B1
10. Papadakis Nikolaos G., Wilkinson Adam A., Carpenter T. Adrian, Hall Laurance D. (1997). A general method for measurement of the time integral of variant magnetic field gradients: Application to 2D spiral imaging, Magnetic Resonance Imaging, Volume 15, Issue 5, Pages 567-578, ISSN 0730-725X
11. Duyn Jeff H., Yang Yihong, Frank Joseph A., van der Veen Jan Willem (1998). Simple Correction Method for k-Space Trajectory Deviations in MRI, Journal of Magnetic Resonance, Volume 132, Issue 1, Pages 150-153, ISSN 1090-7807
12. Liu H., Matson G. B. (2014). Accurate Measurement of Magnetic Resonance Imaging Gradient Characteristics. Materials (Basel);7(1):1–15. doi:10.3390/ma7010001
13. Dale BM, Duerk JL. The Use of Measured K-space Trajectory For Reconstruction of Radial MRI Data; Proceedings of the 10th Meeting of the ISMRM; Honolulu, HI. 2002.p. 2334.
14. Peters DC, Derbyshire JA, McVeigh ER. Centering the projection reconstruction trajectory: Reducing gradient delay errors. Magn. Reson. Med. 2003;50(1):1–6.
15. Reeder SB, Atalar E, Faranesh AZ, McVeigh ER. Referenceless interleaved echo-planar imaging. Magn. Reson. Med. 1999;41(1):87–94.
16. Onodera T, Matsui S, Sekihara K, Kohno H. A Method of measuring field-gradient modulation shapes. Applications to high-speed NMR spectroscopic imaging. J. Phys E: Sci Instrum. 1987;20:416–419.
17. Takahashi A, Peters T. Compensation of multi-dimensional selective excitation pulses using measured k-space trajectories. Magn. Reson. Med. 1995;34(3):446–456.
18. Alley MT, Pineda AR, Bammer R, Markl M, Pelc NJ. A Method for MR Eddy Current Characterization and Compensation; Proceedings of the 11th Meeting of the ISMRM; Toronto, Canada. 2003.p. 1019.
19. Vannesjo S. J., Haeberlin M., Kasper L., Pavan M., Wilm B. J., Barmet C., Pruessmann K. P. (2013). Gradient system characterization by impulse response measurements with a dynamic field camera. Magn Reson Med, 69: 583-593. doi:10.1002/mrm.24263
20. Campbell-Washburn A. E., Xue H., Lederman R. J., Faranesh A. Z., Hansen M. S. (2016). Real-time distortion correction of spiral and echo planar images using the gradient system impulse response function. Magn Reson Med.;75(6):2278–2285. doi:10.1002/mrm.25788
21. Berzl Martin, Pfeil, Antoine, Meyer, Craig, Campbell-Washburn, Adrienne, Körzdörfer, Gregor, Nittka, Mathias, Maier, Andreas, Pfeuffer, Josef (2017). Improved spiral trajectory correction using the gradient impulse response function (GIRF) with application to MR Fingerprinting, Proc. Intl. Soc. Mag. Reson. Med. 25
22. Robison, R. K., Devaraj, A. and Pipe, J. G. (2010). Fast, simple gradient delay estimation for spiral MRI. Magn. Reson. Med., 63: 1683-1690. doi:10.1002/mrm.22327
23. Jiang W, Larson P. E. Z., Lustig M. (2018). Simultaneous auto‐calibration and gradient delays estimation (SAGE) in non‐Cartesian parallel MRI using low‐rank constraints. Magn Reson Med.; 80: 2006– 2016. https://doi.org/10.1002/mrm.27168
24. Glover G. H. (1999). Simple analytic spiral K‐space algorithm. Magn. Reson. Med., 42: 412-415. doi:10.1002/(SICI)1522-2594(199908)42:2<412::AID-MRM25>3.0.CO;2-U
25. Hardy Christopher J., Cline Harvey E. (1989). Broadband nuclear magnetic resonance pulses with two‐dimensional spatial selectivity, Journal of Realized Physics 66:4, 1513-1516
26. King K. F., Foo T., Crawford C. R. (1995). Optimized gradient waveforms for spiral scanning. Magn. Reson. Med., 34: 156-160. doi:10.1002/mrm.1910340205
27. Brodsky E. K., Samsonov A. A., Block W. F. (2009), Characterizing and correcting gradient errors in non-cartesian imaging: Are gradient errors linear time-invariant (LTI)?. Magn Reson Med. 2009;62(6):1466–1476. doi:10.1002/mrm.22100
28. Alok Dutt (1993). Fast Fourier Transforms for Non-Equispaced Data. Ph.D. Dissertation. Yale University, New Haven, CT, USA. UMI Order No. GAX93-29344
29. Liu Q. H., Nguyen N. (1998). Nonuniform fast Fourier transform (NUFFT) algorithm and its applications, IEEE Antennas and Propagation Society International Symposium. 1998 Digest. Antennas: Gateways to the Global Network. Held in conjunction with: USNC/URSI National Radio Science Meeting (Cat. No.98CH36, Atlanta, GA, 1998, pp. 1782-1785 vol.3. doi: 10.1109/APS.1998.690967
30. Lustig M. and Pauly J. M. (2010). SPIRiT: Iterative self‐consistent parallel imaging reconstruction from arbitrary k‐space. Magn. Reson. Med., 64: 457-471. doi:10.1002/mrm.22428
31. Fessler Jeffrey, Sutton Brad (2001). A Min-Max Approach to the Multidimensional Nonuniform FFT: Application to Tomographic Image Reconstruction. IEEE International Conference on Image Processing. 1. 706 - 709 vol.1. 10.1109/ICIP.2001.959143.
32. Pipe, J. G. and Menon, P. (1999), Sampling density compensation in MRI: Rationale and an iterative numerical solution. Magn. Reson. Med., 41: 179-186. doi:10.1002/(SICI)1522-2594(199901)41:1<179::AID-MRM25>3.0.CO;2-V
33. Hoge, R. D., Kwan, R. K. and Bruce Pike, G. (1997), Density compensation functions for spiral MRI. Magn. Reson. Med., 38: 117-128. doi:10.1002/mrm.1910380117
34. Bernstein, Matt A.; King, Kevin F.; Zhou, Xiaohong Joe. Handbook of MRI Pulse Sequence. Elsevier academic press; 2004. p. 319-323.
35. Martín Abadi, et al. (2015). TensorFlow: Large-scale machine learning on heterogeneous systems. Software available from tensorflow.org.
36. Kingma D. P., Ba J. L. (2015). Adam: A Method for Stochastic Optimization. International Conference on Learning Representations, 1–13.
37. Ma D., Gulani V., Seiberlich N., et al. (2013). Magnetic resonance fingerprinting. Nature;495(7440):187–192. doi:10.1038/nature11971
38. Jiang, Y., Ma, D., Seiberlich, N., Gulani, V. and Griswold, M. A. (2015), MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn. Reson. Med., 74: 1621-1631. doi:10.1002/mrm.25559
39. Keenan K, Stupic K, Boss M, et al. Multi-Site, Multi-Vendor Comparison of T1 Measurement Using ISMRM/NIST System Phantom. Proceeding 24th Annu. Meet. ISMRM; Singapore. 2016. p. 3290
Figures